必須掌握各個概念的定義。從定義中，深入的理解概念，以及發掘概念之間的相互聯絡。

導數&微分

微積分有兩種定義：
1、古典微積分
這是一種直觀、便於理解的定義。首先定義微分是微小變化量。比如函式y=f(x)中dx是x的微小變化量，那麼dy就是dx對應的y的微小變化。導數也就從中得到了定義：是兩個微小變數的比值=dy/dx。所以導數也被稱為微商。這是古典定義，可以看出是非常容易理解的。

2、基於極限的微積分。
古典微積分雖然直觀但是不夠嚴謹，因此全新的微積分定義被髮明瞭，這就是基於極限的微積分。導數首先被嚴格的定義為了一種極限：

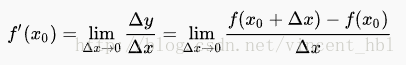
然後微分在導數的基礎上得到了定義：（來源於維基）

從定義可以看出，微分dy被定義為了一個函式，這個函式是y真實變化量Δy的一個線性近似。Δy和Δx是非線性關係，但是dy和Δx是線性關係。那麼在點x處，且Δx趨近於0時，線性關係中的A值就是函式在x處的導數。所以有：

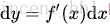
可以看出這裡dy也可以像古典微積分定義的微分那樣被理解為一個微小變化量，只不過其中的含義更深刻了。

不定積分

不定積分的定義
首先明確一點，一定要區分不定積分和定積分。從概念上說，這是兩個定義完全不同的東西。
不定積分是給定一個函式，求該函式的帶有一個常數項的原函式的過程。所以不定積分的結果是一個函式。相比之下，定積分得到的結果是一個數值。

計算不定積分的方法：

1、基本積分表
2、不定積分滿足加性、齊性。（線性對映的兩個性質！）
3、第一換元法

暫時把這個定積分看成不定積分。嚴格的講，積分表示式中dx這個符號是整體的一部分，並不表示微分的概念。然而，如果把dx當做微分，根據微分的定義，進行第一換元法中的變化就是合情合理的了，因為這個過程其實是將一個微分替換為另一個微分。
4、第二換元法
第二換元法是第一換元法的相反過程。把dx分解，x可以看做是一個函式，然而x可以被變換為任何的函式，所以第二換元法更加靈活和困難。
5、分部積分法

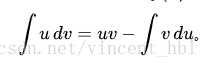
這是由導數的乘法法則來的。