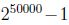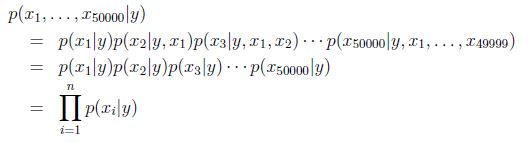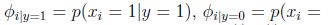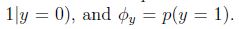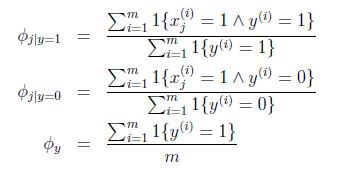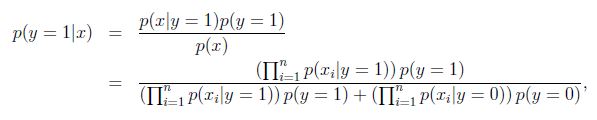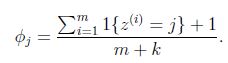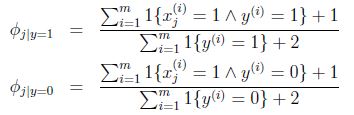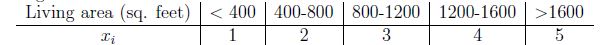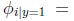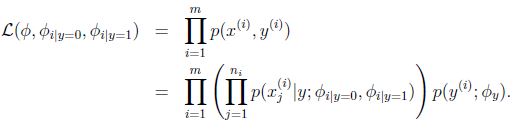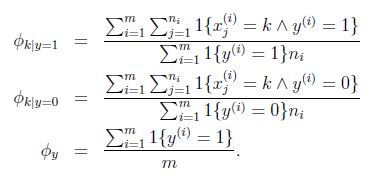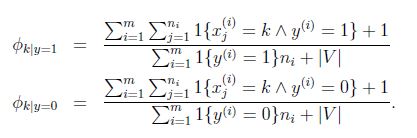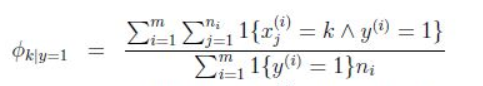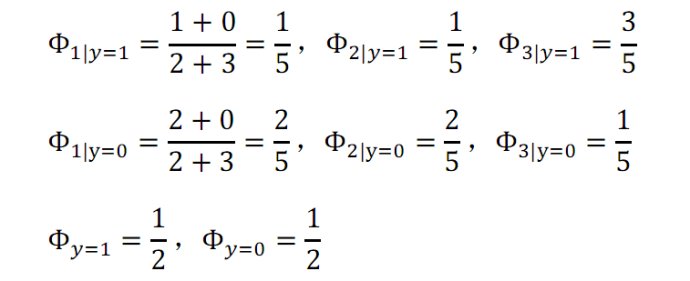樸素貝葉斯.Laplace平滑.多項式事件模型
《Andrew Ng 機器學習筆記》這一系列文章文章是我再觀看Andrew Ng的Stanford公開課之後自己整理的一些筆記,除了整理出課件中的主要知識點,另外還有一些自己對課件內容的理解。同時也參考了很多優秀博文,希望大家共同討論,共同進步。
網易公開課地址:http://open.163.com/special/opencourse/machinelearning.html
參考博文:http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html(樸素貝葉斯分類)
http://blog.sina.com.cn/s/blog_8a951ceb0102wbbv.html
本篇博文涉及課程五:樸素貝葉斯演算法
本課主要內容有:
(1)樸素貝葉斯演算法
(2)Laplace平滑
(3)多項式事件模型
樸素貝葉斯演算法(NB)
在GDA模型中,特徵向量x是連續的實數向量,當x是離散值時,我們就需要採用樸素貝葉斯演算法。
樸素貝葉斯的思想:對於給出的待分類項,求解在此項出現的條件下各個類別出現的概率,哪個最大,就認為此待分類項屬於哪個類別。
樸素貝葉斯演算法的應用,最常見的是文字分類問題,例如郵件是否為垃圾郵件。
對於文字分類問題來說,使用向量空間模型(vector space model,VSM)來表示文字。
什麼是向量空間模型?
首先,我們需要有一個詞典,詞典的來源可以是現有的詞典,也可以是從資料中統計出來的詞典,對於每個文字,我們用長度等於詞典大小的向量表示,如果文字包含某個詞,該詞在詞典中的索引為index,則表示文字的向量的index出設為1,否則為0。
下面以垃圾郵件分類問題為例進行說明:
將郵件作為輸入特徵,與已有的詞典進行比對,如果出現了該詞,則把向量的xi=1,否則xi=0,例如:

我們要對p(x|y)建模,但是假設我們的詞典有50000個詞,那麼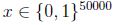
因此有:
模型引數包括:
極大似然函式的對數函式為:
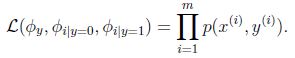
得到引數的最大似然估計值:
對於新樣本,我們就可以按照如下公式計算其概率值:
Laplace平滑
樸素貝葉斯存在的問題:
假設在一封郵件中出現了一個以前郵件從來沒有出現的詞,在詞典的位置是35000,那麼得出的最大似然估計為:
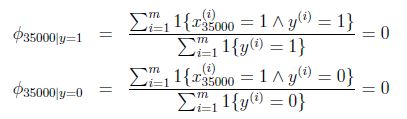
也就是說,如果一個單詞在之前的垃圾郵件和非垃圾郵件中都部曾出現過,那麼,樸素貝葉斯模型認為這個詞在任何一封郵件出現的概率為0.
如果,這封郵件是一封垃圾郵件,但通過公式得到的是:
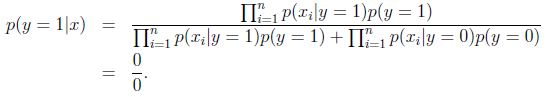
這樣得到的結果並不是很合理,因為我們不能因為某個事件過去沒有出現過,就判斷該事件出現的概率為0,。
拉普拉斯平滑(Laplace Smoothing)又被稱為加1平滑,是比較常用的平滑方法。平滑方法的存在是為了解決零概率問題。、
Laplace的解決方法是:
對於一個隨機變數z,它的取值範圍是{1,2,3...,k},對於m次試驗的觀測結果{z(1),z(2),...z(m))},極大似然估計按照下式計算:
使用了Laplace之後:
即在分子上+1,在分母上+變數能取到的個數。
因此,在樸素貝葉斯問題,通過laplace平滑修正後:
多項式事件分佈
上面的這種基本的樸素貝葉斯模型叫做多元伯努利事件模型,該模型有多種擴充套件,一種是每個分量的多值化,即將p(xi|y)由伯努利分佈擴充套件到多項式分佈;還有一種是將連續變數值離散化。例如以房屋面積為例:
還有一種,與多元伯努利有較大區別的樸素貝葉斯模型,就是多項式事件模型。
多項式事件模型改變了特徵向量的表示方法:
在多元伯努利模型中,特徵向量的每個分量代表詞典中該index上的詞語是否在文字中出現過,其取值範圍為{0,1},特徵向量的長度為詞典的大小。
而在多項式事件模型中,特徵向量中的每個分量的值是文字中處於該分量位置的單詞在詞典中的索引,其取值範圍是{1,2,...,|V|},|V|是詞典的大小,特徵向量的長度為文字中單詞的數量。
例如:在多元伯努利模型下,一篇文字的特徵向量可能如下:
在多項式事件模型下,這篇文字的特徵向量為:
一篇文字產生的過程是:
1、確定文字類別
2、以相同的多項式分佈在各個位置上生成詞語。
例如:x1是由服從p(x1|y)的多項式分佈產生的,x2是獨立與x1的並且來自於同一個多項式分佈,同樣的,產生x3,x4,一直到xn。
因此,所有的這個資訊的概率是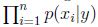
模型的引數為:
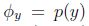
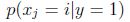
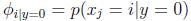
引數在訓練集上的極大似然函式:
引數的最大似然估計為:
應用laplace平滑,分子加1,分母加|V|,得到:
對於式子:
分子的意思是對訓練集合中的所有垃圾郵件中詞k出現的次數進行求和。
分母的含義是對訓練樣本集合進行求和,如果其中的一個樣本是垃圾郵件(y=1),那麼就把它的長度加起來,所以分母的含義是訓練集合中所有垃圾郵件的詞語總長。
所以這個比值的含義就是在所有垃圾郵件中,詞k所佔的比例。
注意這個公式與多元伯努利的不同在於:這裡針對整體樣本求的φk|y=1 ,而多遠伯努利裡面針對每個特徵求的φxj=1|y=1 ,而且這裡的特徵值維度不一定是相同的。
舉例說明多項式事件模型:
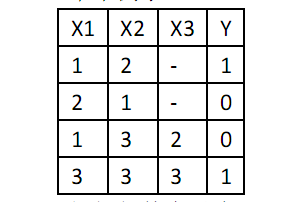
假設郵件中有a,b,c三個詞,他們在詞典的位置分別是1,2,3,第一封裡面內容為a,b,第二封為b,a;第三封為a,c,b,第四封為c,c,c。
Y=1是垃圾郵件。
因此,我們有:
那麼,我們可得:
假如有一封信的郵件,內容為b,c。那麼它的特徵向量為{2,3},我們可得:
那麼該郵件為垃圾郵件概率是0.6。
相關推薦
樸素貝葉斯.Laplace平滑.多項式事件模型
《Andrew Ng 機器學習筆記》這一系列文章文章是我再觀看Andrew Ng的Stanford公開課之後自己整理的一些筆記,除了整理出課件中的主要知識點,另外還有一些自己對課件內容的理解。同時也參考了很多優秀博文,希望大家共同討論,共同進步。 網易公開課地址:htt
樸素貝葉斯 拉普拉斯平滑(Laplace Smoothing)
轉自:https://blog.csdn.net/qq_25073545/article/details/78621019拉普拉斯平滑(Laplace Smoothing)又被稱為加 1 平滑,是比較常用的平滑方法。平滑方法的存在時為了解決零概率問題。背景:為什麼要做平滑處理
樸素貝葉斯的三個常用模型:高斯、多項式、伯努利
樸素貝葉斯是一個很不錯的分類器,在使用樸素貝葉斯分類器劃分郵件有關於樸素貝葉斯的簡單介紹。 若一個樣本有n個特徵,分別用x1,x2,…,xnx1,x2,…,xn表示,將其劃分到類ykyk的可能性P(yk|x1,x2,…,xn)P(yk|x1,x2,…,xn)為:
分類-3-生成學習-3-樸素貝葉斯模型、laplace平滑、多元伯努利事件模型、多項式事件模型
多元伯努利事件模型( multi-variate Bernoulli event model) 在 GDA 中,我們要求特徵向量 x 是連續實數向量。如果 x 是離散值的話,可以考慮採用樸素貝葉斯的分類方法。 假如要分類垃圾郵件和正常郵件。 我們用
樸素貝葉斯分類--多項式模型
本文來自於百度文庫https://wenku.baidu.com/view/70c98707abea998fcc22bcd126fff705cc175c6b.html 文中公式多有問題,還需要重新編輯,但整體而言不影響理解。 樸素貝葉斯分類--多項式模型 1. 多項式模
機器學習:貝葉斯分類器,樸素貝葉斯,拉普拉斯平滑
數學基礎: 數學基礎是貝葉斯決策論Bayesian DecisionTheory,和傳統統計學概率定義不同。 頻率學派認為頻率是是自然屬性,客觀存在的。 貝葉斯學派,從觀察這出發,事物的客觀隨機性只是觀察者不知道結果,也就是觀察者的知識不完備,對於知情者而言,事物沒有隨機性,隨機
sklearn實現多項式樸素貝葉斯
以下程式碼是利用sklearn自帶的資料庫來實現對垃圾郵件的分類,關於樸素貝葉斯實現分類的原理網上有很多教程,這裡不再贅述,直接上程式碼: # --*-- coding:utf-8 --*-- from sklearn.datasets import fetch_20newsgroups
樸素貝葉斯模型、推導、拉普拉斯平滑
參考書籍:《統計學習方法》,cs229講義,其他。 1、樸素貝葉斯 1.1、樸素貝葉斯模型 樸素貝葉斯:基於貝葉斯定理與特徵條件獨立假設的分類方法。注意兩個點,一個是貝葉斯定理,另一個是條件獨立假設,後面會用到,該方法用來進行分類,即:給定輸入變數x,輸出類別標記y 先定
深入理解Spark ML:多項式樸素貝葉斯原理與原始碼分析
貝葉斯估計 如果一個給定的類和特徵值在訓練集中沒有一起出現過,那麼基於頻率的估計下該概率將為0。這將是一個問題。因為與其他概率相乘時將會把其他概率的資訊統統去除。所以常常要求要對每個小類樣本的概率估計進行修正,以保證不會出現有為0的概率出現。常用到
<Machine Learning in Action >之二 樸素貝葉斯 C#實現文章分類
options 直升機 water 飛機 math mes 視頻 write mod def trainNB0(trainMatrix,trainCategory): numTrainDocs = len(trainMatrix) numWords =
(筆記)斯坦福機器學習第六講--樸素貝葉斯
span || -h 沒有 height 單純 去除 變量 logistic 本講內容 1. Naive Bayes(樸素貝葉斯) 2.Event models(樸素貝葉斯的事件模型) 3.Neural network (神經網絡) 4.Support vector mac
基於的樸素貝葉斯的文本分類(附完整代碼(spark/java)
ava -s for 轉換成 模型保存 ext js rgs cti txt 本文主要包括以下內容: 1)模型訓練數據生成(demo) 2 ) 模型訓練(spark+java),數據存儲在hdfs上 3)預測數據生成(demo) 4)使用生成的模型進行文本分類。 一
樸素貝葉斯分類算法
貝葉斯 樸素 之前有次考試考的是手工計算樸素貝葉斯的分類。當時沒答對,後來搞明白了,不久又忘得差不多了。所以寫個例子在這兒記一下。先推導一下貝葉斯公式:假定我們觀察到兩個事件都發生了,記做P(AB),那麽我們既可以認為先發生了事件A,在此基礎上又發生了事件B,也可以認為先發生了事件B,在此基礎上又發生
利用樸素貝葉斯(Navie Bayes)進行垃圾郵件分類
判斷 ase create numpy water 向量 not in imp img 貝葉斯公式描寫敘述的是一組條件概率之間相互轉化的關系。 在機器學習中。貝葉斯公式能夠應用在分類問題上。這篇文章是基於自己的學習所整理。並利用一個垃圾郵件分類的樣例來加深對於理論的理解
樸素貝葉斯分類算法介紹及python代碼實現案例
urn bus 人的 元素 1.2 -s index 代碼 步驟 樸素貝葉斯分類算法 1、樸素貝葉斯分類算法原理 1.1、概述 貝葉斯分類算法是一大類分類算法的總稱 貝葉斯分類算法以樣本可能屬於某類的概率來作為分類依據 樸素貝葉斯分類算法是貝葉斯分類算法中最簡單的一種 註:
樸素貝葉斯算法資料整理和PHP 實現版本
樸素貝葉斯樸素貝葉斯算法簡潔http://blog.csdn.net/xlinsist/article/details/51236454 引言先前曾經看了一篇文章,一個老外程序員寫了一些很牛的Shell腳本,包括晚下班自動給老婆發短信啊,自動沖Coffee啊,自動掃描一個DBA發來的郵件啊, 等等。於是我也想
javascript實現樸素貝葉斯分類與決策樹ID3分類
.com 訓練集 this ice map ive sum length roc 今年畢業時的畢設是有關大數據及機器學習的題目。因為那個時間已經步入前端的行業自然選擇使用JavaScript來實現其中具體的算法。雖然JavaScript不是做大數據處理的最佳語言,相比還沒有
機器學習系列——樸素貝葉斯分類器(二)
表示 -h line log ima 條件 code 樸素貝葉斯 spa 貝葉斯定理: 其中: 表示事件B已經發生的前提下,事件A發生的概率,叫做事件B發生下事件A的條件概率。其基本求解公式為:。 機器學習系列——樸素貝葉斯分類器(二)
樸素貝葉斯
9.png 貝葉斯 分詞 世界 最大 log 制造 技術分享 規律 樸素貝葉斯分類是基於貝葉斯概率的思想,假設屬性之間相互獨立,求得各特征的概率,最後取較大的一個作為預測結果(為了消弱罕見特征對最終結果的影響,通常會為概率加入權重,在比較時加入閾值)。樸素貝葉斯是較為簡
樸素貝葉斯-Numpy-對數似然
連續 數學 learn append ocs 似然 mtr 詞匯 reat 《Machine Learning in Action》 為防止連續乘法時每個乘數過小,而導致的下溢出(太多很小的數相乘結果為0,或者不能正確分類) 訓練: def trainN