尤拉降冪(尤拉-費馬定理)
map<ll,ll> map_phi; ll get_phi(ll n) { ll res = n,a = n; for(ll i = 2;i * i <= n;++i){ if(a % i == 0){ res = res / i * (i - 1); while(a % i == 0) a /= i; } } if(a > 1) res = res / a * (a - 1); return res; } ll fpow_mod(ll a,ll b,ll mod) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1; } return res; } void init(ll mod) { while(mod != 1){ map_phi[mod] = get_phi(mod); mod = map_phi[mod]; } map_phi[1] = 1; }
尤拉定理: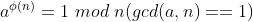
所以對於高位的取模,我們可以用尤拉公式來降冪(根據尤拉公式將滿足尤拉公式的部分轉化成1,即可進行降冪操作)
小技巧:可以通過用map打表來降低時間複雜度
相關推薦
尤拉降冪(尤拉-費馬定理)
map<ll,ll> map_phi; ll get_phi(ll n) { ll res = n,a = n; for(ll i = 2;i * i <= n;++i){ if(a % i == 0){
演算法學習->尤拉降冪(尤拉+快速冪)
一、尤拉函式 尤拉函式是用來求n的質因數的個數。 ll ouler(ll n){ ll ans=n,a=n; for(ll i=2;i*i<=a;i++){
POJ 2420 A Star not a Tree?(二維費馬點)
題目:就是求多邊形的費馬點,輸出最小的距離。 做法:隨機化變步長貪心法(模擬退火???) 首先隨機選出一點,我直接取了0,0 然後選定一個步長,往4個方向開始找,如果更優則繼續,否則降低步長,直到滿足題目要求精度 也可以8個方向等等 #include<iostre
【FZU - 1759】Super A^B mod C (數論,快速冪,快速乘,尤拉降冪,指數迴圈節,模板)
題幹: Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000). Input There are mult
公鑰密碼 之 素數,費馬定理與尤拉定理
素數 素數是我們中學就知道的知識,關於概念就不再贅述,我們來給出形式化的定義: 任意整數a > 1都可以唯一的因子分解為多個素數的積,設P為所有素數的集合,則對任意正整數a可唯一表示為: , 其中每一個 特性: 若,定義k=ab
逆元 + 費馬定理 + 尤拉定理
一,逆元: 先讓我們考慮如何求解線性同餘方程 :a * x ≡ b ( mod m ) (1)(x為一個變數)。 對於方程:a * x = b ,由於a存在倒數1/a ( a * y = 1,y
hiho 1298 數論·五 尤拉函式 (尤拉函式篩選板子)
描述 小Hi和小Ho有時候會用密碼寫信來互相聯絡,他們用了一個很大的數當做金鑰。小Hi和小Ho約定了一個區間[L,R],每次小Hi和小Ho會選擇其中的一個數作為金鑰。 小Hi:小Ho,這次我們選[L,R]中的一個數K。 小Ho:恩,小Hi,這個K是多少啊? 小Hi:這個K嘛,不如這一次小Ho你自己想辦法
費馬定理&歐拉定理
。。 因數 證明 其中 return 一個 ios 質數 並且 費馬定理: ap≡a(mod p) 其中p為質數,且a不是p的倍數 證明: 。。。。。 歐拉定理: aφ(p)≡1(mod p) φ(x)(歐拉函數)
無向圖歐拉道路(歐拉回路)的判定與路徑打印
clu clas 檢查 names 連通圖 思路 return space 計算 歐拉道路描述的是無向圖的一個頂點出發的一條道路能夠經過每條邊恰好一次 歐拉回路指的是任意點出發都滿足上述性質 如果一個圖是歐拉道路或者歐拉回路,必須滿足兩個條件 第一個條件,這個圖是連通圖 第
迪傑斯特拉演算法(可列印最短路徑)(資料結構題集C語言版7.11)
轉自 https://blog.csdn.net/cxllyg/article/details/7604812 #include <iostream> #include <iomanip> #include <string> usi
HDU 4704 Sum (費馬定理+快速冪)
Sum Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) Total Subm
費馬素數(費馬質數)
0x01 普遍形式 費馬素數也叫費馬質數。 其中 n 為非負整數。 0x02 歷史 法國數學家費馬於1640年提出了以下猜想: 可以看出,前4個是質數,因為第5個數實在太大了,費馬認為是質數。 由此提出(費馬沒給出證明),形如 的數都是質數的猜想。後來人
獲取多選下拉框(select標籤設定multiple屬性)的值
<select multiple>不能直接獲取value,需要藉助該元素的options屬性。如下: <select id="select" multiple> <option value="1">1111</option> &
結合zTree實現 Js/jQuery/Html 下拉樹(下拉框嵌入樹結構)
一、效果圖 二、專案結構 三、使用方法 (1)引入 jQuery 包,下載地址 (2)引入 zTree 包,下載地址 (3)引入 tree-select.js (4)$("#id").treeSelect(data); 一句話搞定 四、實現原始
機器學習中的數學:洛必達法則(能力工場小馬哥)
轉載 什麽 機器學習 數學 比賽 技術 函數 著作權 不存在 通俗地講,求極限的本質是分子與分母“比階”,比誰的速度快。 就像分子分母在跑道上進行趨於0或者無窮的賽跑,我們旁觀者想搞清楚他們1.誰贏了?(極限是大於一還是小於一?)2.他們是差不多同時撞線還是領先者領先
關於SimHash去重原理的理解(能力工場小馬哥)
閱讀目錄 1. SimHash與傳統hash函式的區別 2. SimHash演算法思想 3. SimHash流程實現 4. SimHash簽名距離計算 5. SimHash儲存和索引 6. SimHash儲存和索引 7. 參考內容
OpenCV3.3—影象增強(方法:伽馬變換)
1. 伽馬變換 伽馬變換主要用於影象的校正,將灰度過高或者灰度過低的圖片進行修正,增強對比度。變換公式就是對原影象上每一個畫素值做乘積運算: 伽馬變換對影象的修正作用其實就是通過增強低灰度或高灰度的細節實現的,從伽馬曲線可以直觀理解: γ值以1為分界,值越小,對影象
bzoj 2111: [ZJOI2010]Perm 排列計數 (dp+盧卡斯定理)
dir code def -1 text eight clu 階乘 typedef bzoj 2111: [ZJOI2010]Perm 排列計數 1 ≤ N ≤ 10^6, P≤ 10^9 題意:求1~N的排列有多少種小根堆 1: #i
POJ 1426 Find The Multiple(數論——中國同余定理)
定義 十進制 pro desc decimal tput one return solution 題目鏈接: http://poj.org/problem?id=1426 Description Given a positive integer n, write a pro
【51Nod 1103】N的倍數(字首和,抽屜定理)詳細!!
Description 一個長度為N的陣列A,從A中選出若干個數,使得這些數的和是N的倍數。 例如:N = 8,陣列A包括:2 5 6 3 18 7 11 19,可以選2 6,因為2 + 6 = 8,是8的倍數。 先欣賞一下兩位大佬的程式碼 字首和
