這原是知乎上的一遍問答，我也在CSDN上看到了同樣的轉載博文，可是由於圖片轉載不過來影響了閱讀，我在這裡重新把影象轉載到了CSDN,供大家閱讀。感謝原作者！

從傅立葉變換到小波變換，並不是一個完全抽象的東西，可以講得很形象。小波變換有著明確的物理意義，如果我們從它的提出時所面對的問題看起，可以整理出非常清晰的思路。

下面我就按照傅立葉-->短時傅立葉變換-->小波變換的順序，講一下為什麼會出現小波這個東西、小波究竟是怎樣的思路。

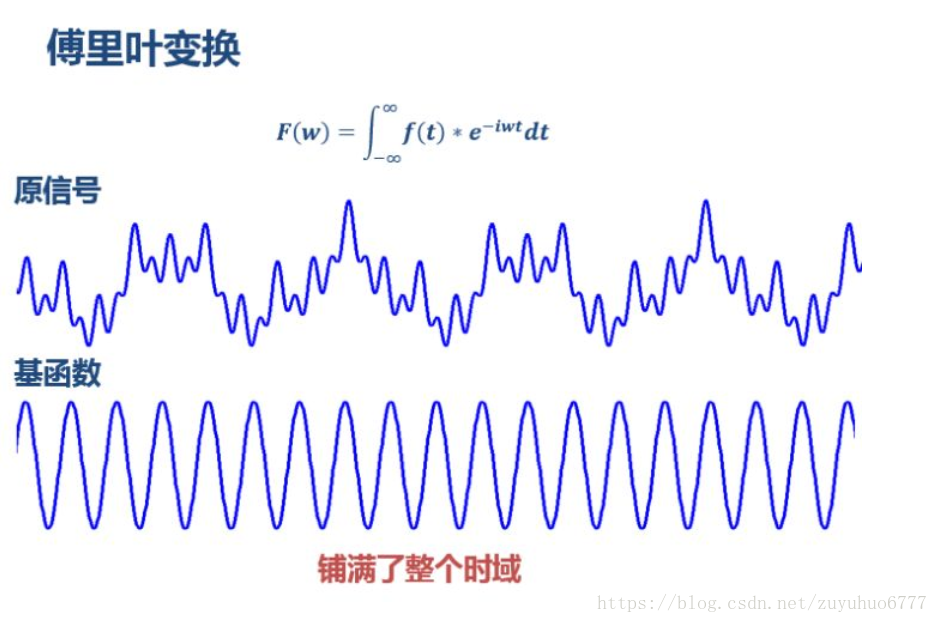
一、傅立葉變換

關於傅立葉變換的基本概念在此我就不再贅述了，預設大家現在正處在理解了傅立葉但還沒理解小波的道路上。

下面我們主要將傅立葉變換的不足。

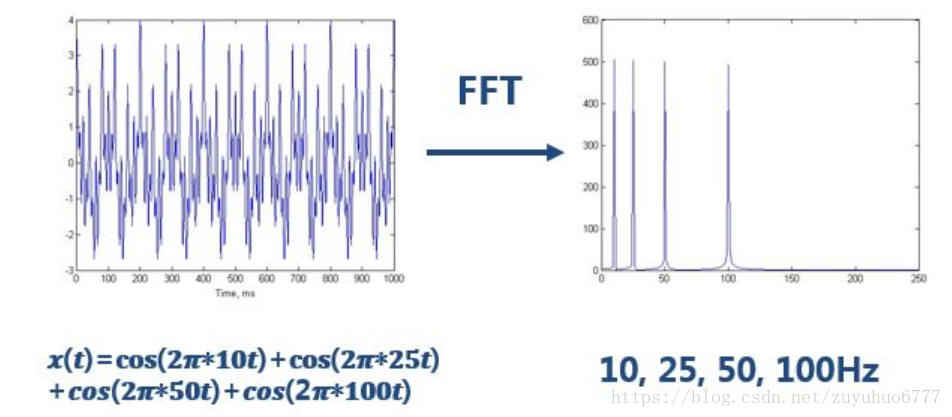
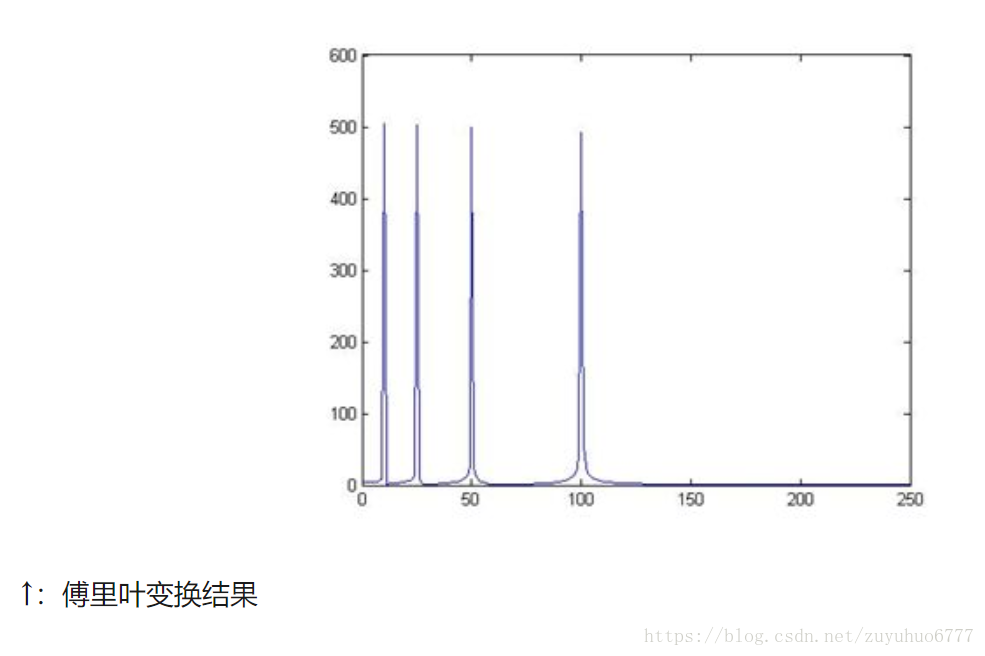
做完FFT（快速傅立葉變換）後，可以在頻譜上看到清晰的四條線，訊號包含四個頻率成分。一切都沒有問題。

但是，如果是頻率隨著時間變化的非平穩訊號呢？

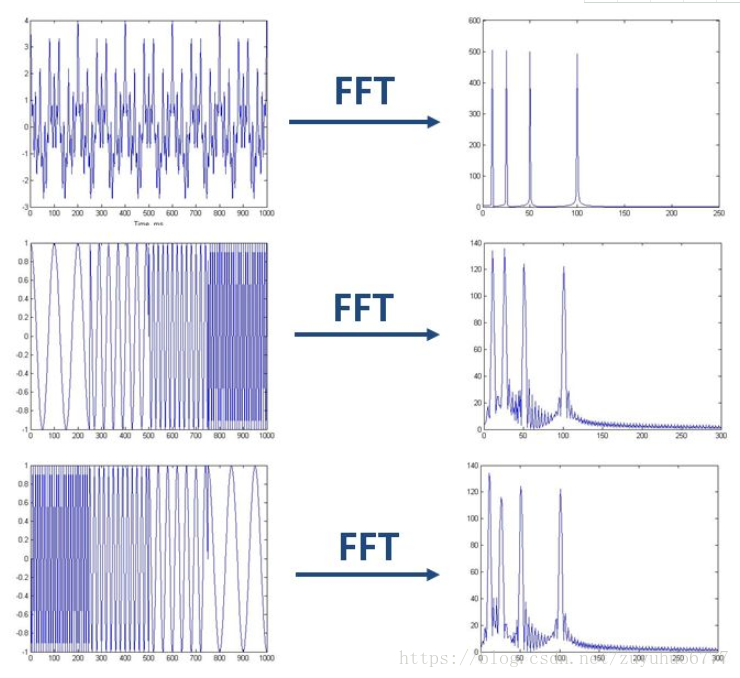
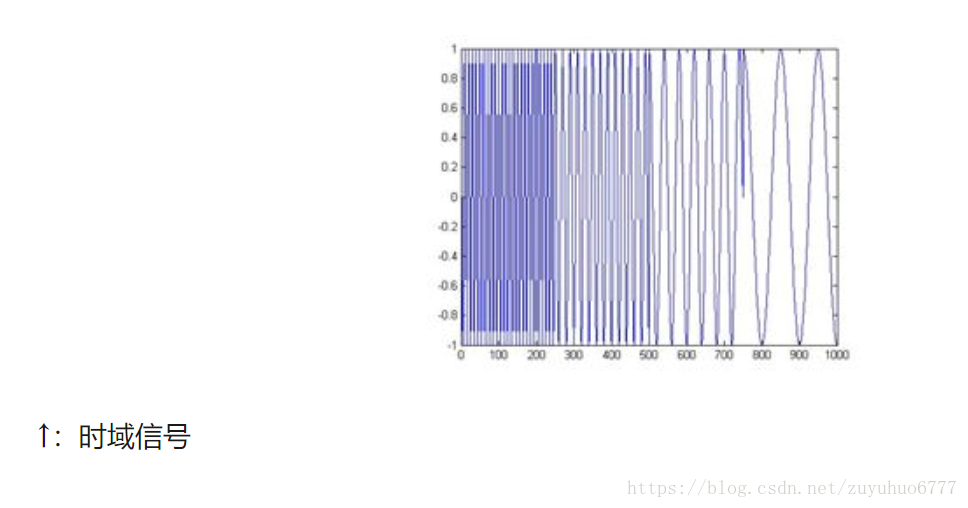
如上圖，最上邊的是頻率始終不變的平穩訊號。而下邊兩個則是頻率隨著時間改變的非平穩訊號，它們同樣包含和最上訊號相同頻率的四個成分。
做FFT後，我們發現這三個時域上有巨大差異的訊號，頻譜（幅值譜）卻非常一致。尤其是下邊兩個非平穩訊號，我們從頻譜上無法區分它們，因為它們包含的四個頻率的訊號的成分確實是一樣的，只是出現的先後順序不同

可見，傅立葉變換處理非平穩訊號有天生缺陷。它只能獲取一段訊號總體上包含哪些頻率的成分，但是對各成分出現的時刻並無所知。因此時域相差很大的兩個訊號，可能頻譜圖一樣。

然而平穩訊號大多是人為製造出來的，自然界的大量訊號幾乎都是非平穩的，所以在比如生物醫學訊號分析等領域的論文中，基本看不到單純傅立葉變換這樣naive的方法。

上圖所示的是一個正常人的事件相關電位。對於這樣的非平穩訊號，只知道包含哪些頻率成分是不夠的，我們還想知道各個成分出現的時間。知道訊號頻率隨時間變化的情況，各個時刻的瞬時頻率及其幅值——這也就是時頻分析。

二、短時傅立葉變換（Short-time Fourier Transform, STFT）

一個簡單可行的方法就是——加窗。“把整個時域過程分解成無數個等長的小過程，每個小過程近似平穩，再傅立葉變換，就知道在哪個時間點上出現了什麼頻率了。”這就是短時傅立葉變換。

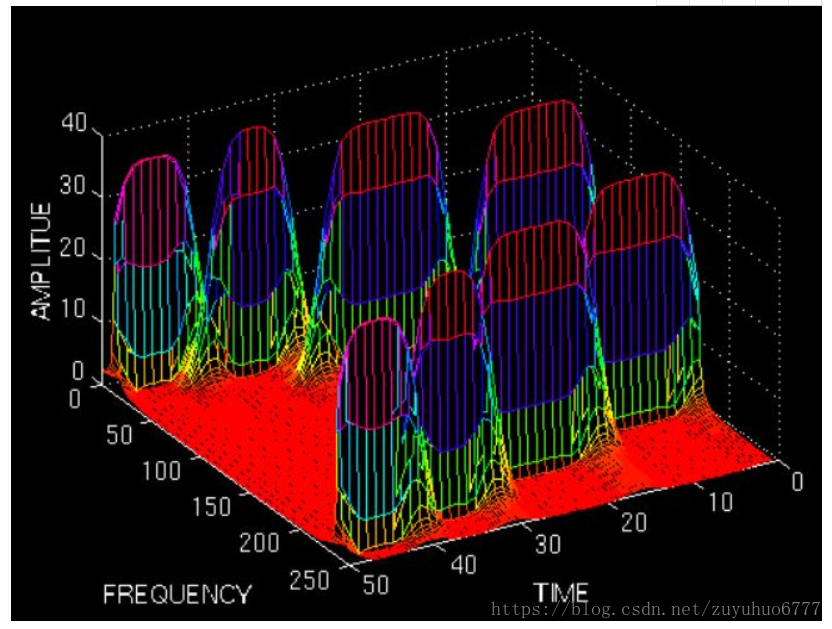
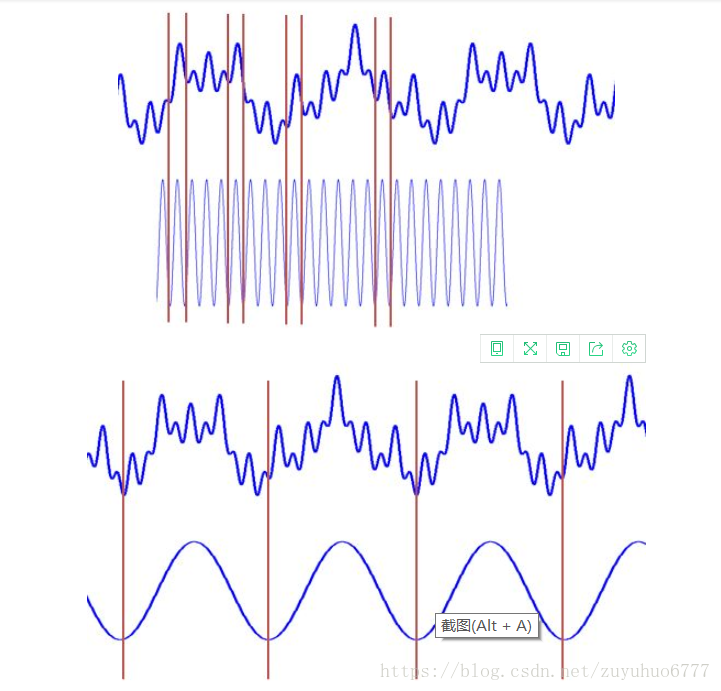
時域上分成一段一段做FFT，不就知道頻率成分隨著時間的變化情況了嗎！用這樣的方法，可以得到一個訊號的時頻圖了：

圖上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四個頻域成分，還能看到出現的時間。兩排峰是對稱的，所以大家只用看一排就行了。

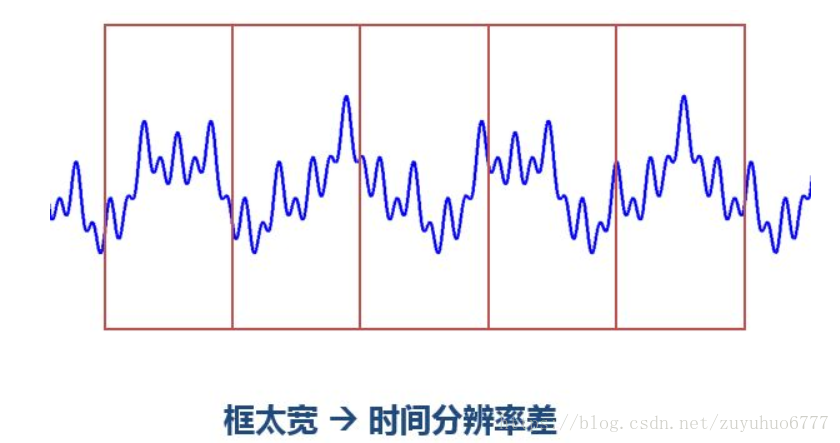
時頻分析結果到手。但是STFT依然有缺陷。使用STFT存在一個問題，我們應該用多寬的窗函式？
窗太寬太窄都有問題：

窗太窄，窗內的訊號太短，會導致頻率分析不夠精準，頻率解析度差。窗太寬，時域上又不夠精細，時間解析度低。

看看例項效果吧：

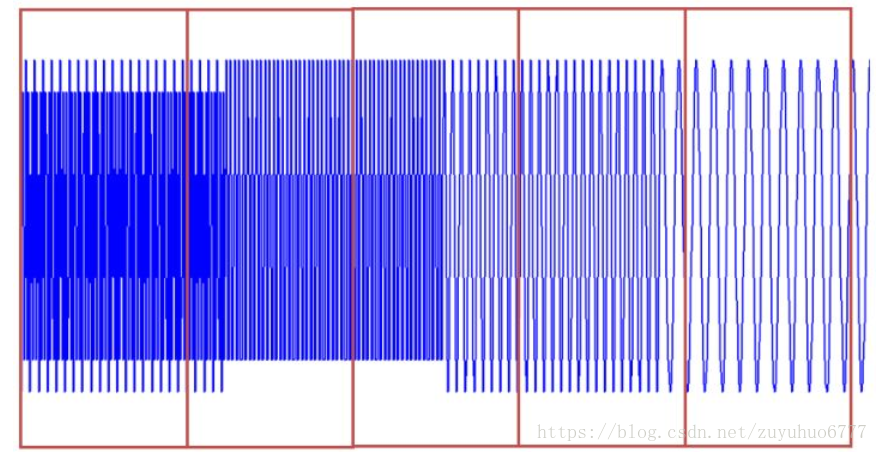
上圖對同一個訊號（4個頻率成分）採用不同寬度的窗做STFT，結果如右圖。用窄窗，時頻圖在時間軸上解析度很高，幾個峰基本成矩形，而用寬窗則變成了綿延的矮山。但是頻率軸上，窄窗明顯不如下邊兩個寬窗精確。

所以窄視窗時間解析度高、頻率解析度低，寬視窗時間解析度低、頻率解析度高。對於時變的非穩態訊號，高頻適合小視窗，低頻適合大視窗。然而STFT的視窗是固定的，在一次STFT中寬度不會變化，所以STFT還是無法滿足非穩態訊號變化的頻率的需求。

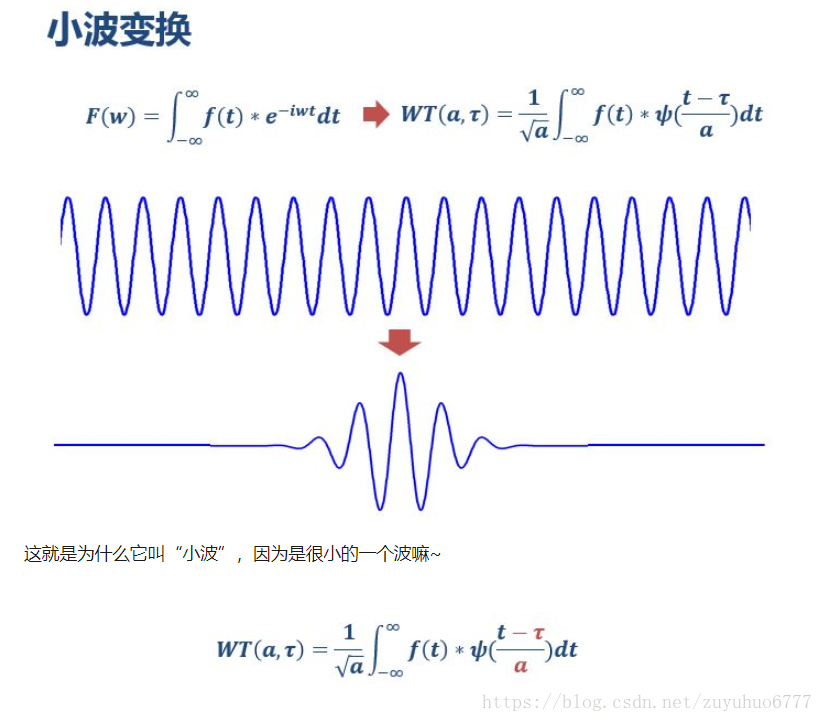
三、小波變換

那麼你可能會想到，讓視窗大小變起來，多做幾次STFT不就可以了嗎？！沒錯，小波變換就有著這樣的思路。
但事實上小波並不是這麼做的（關於這一點，方沁園同學的表述“小波變換就是根據演算法，加不等長的窗，對每一小部分進行傅立葉變換”就不準確了。小波變換並沒有採用窗的思想，更沒有做傅立葉變換。）
至於為什麼不採用可變窗的STFT呢，我認為是因為這樣做冗餘會太嚴重，STFT做不到正交化，這也是它的一大缺陷。

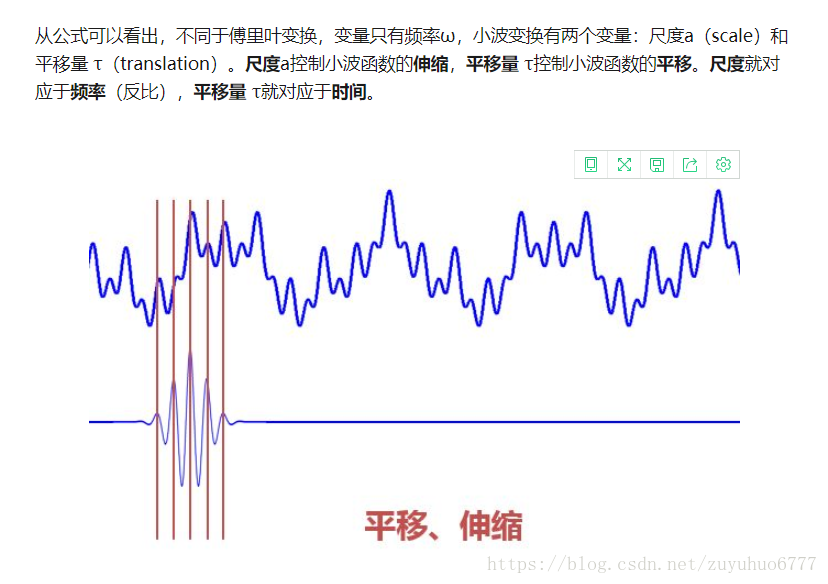
於是小波變換的出發點和STFT還是不同的。STFT是給訊號加窗，分段做FFT；而小波直接把傅立葉變換的基給換了——將無限長的三角函式基換成了有限長的會衰減的小波基。這樣不僅能夠獲取頻率，還可以定位到時間了~

【解釋】
來我們再回顧一下傅立葉變換吧，沒弄清傅立葉變換為什麼能得到訊號各個頻率成分的同學也可以再借我的圖理解一下。
傅立葉變換把無限長的三角函式作為基函式：

這個基函式會伸縮、會平移（其實本質並非平移，而是兩個正交基的分解）。縮得窄，對應高頻；伸得寬，對應低頻。然後這個基函式不斷和訊號做相乘。某一個尺度（寬窄）下乘出來的結果，就可以理解成訊號所包含的當前尺度對應頻率成分有多少。於是，基函式會在某些尺度下，與訊號相乘得到一個很大的值，因為此時二者有一種重合關係。那麼我們就知道訊號包含該頻率的成分的多少。

仔細體會可以發現，這一步其實是在計算訊號和三角函式的相關性。

看，這兩種尺度能乘出一個大的值（相關度高），所以訊號包含較多的這兩個頻率成分，在頻譜上這兩個頻率會出現兩個峰。
以上，就是粗淺意義上傅立葉變換的原理。
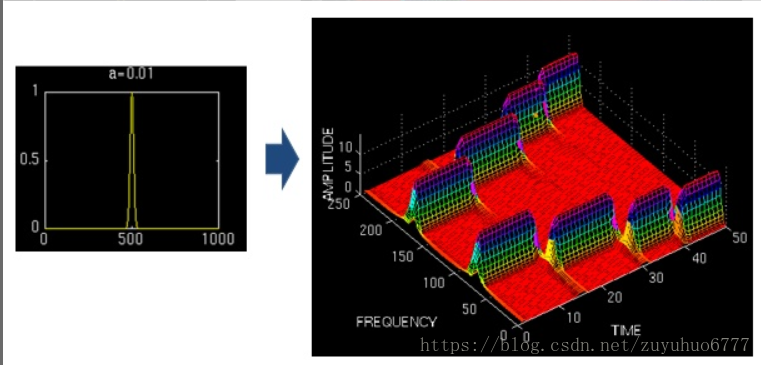
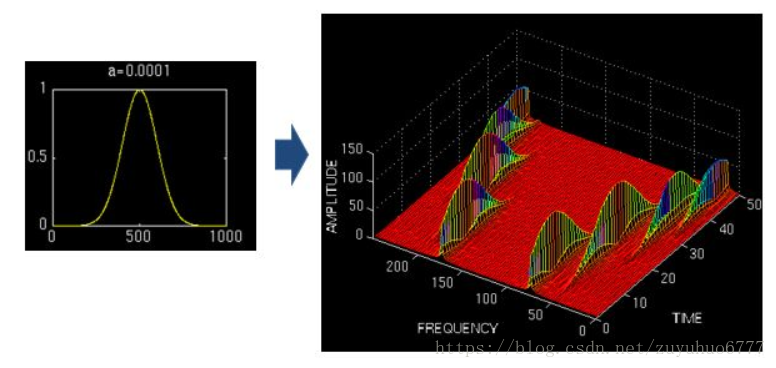
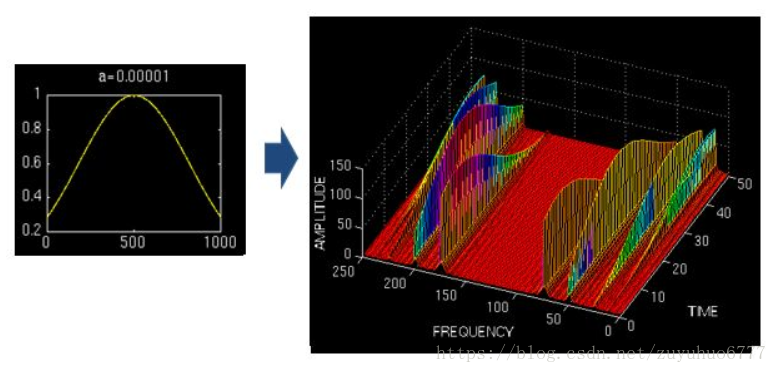
如前邊所說，小波做的改變就在於，將無限長的三角函式基換成了有限長的會衰減的小波基。

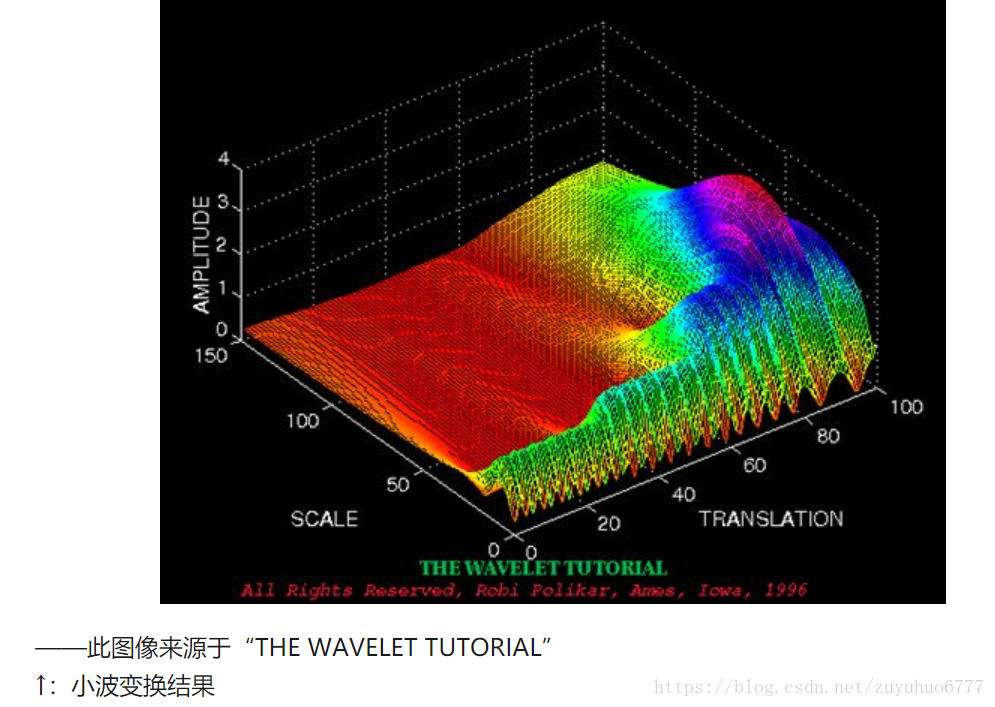
當伸縮、平移到這麼一種重合情況時，也會相乘得到一個大的值。這時候和傅立葉變換不同的是，這不僅可以知道訊號有這樣頻率的成分，而且知道它在時域上存在的具體位置。

而當我們在每個尺度下都平移著和訊號乘過一遍後，我們就知道訊號在每個位置都包含哪些頻率成分。

看到了嗎？有了小波，我們從此再也不害怕非穩定訊號啦！從此可以做時頻分析啦！

做傅立葉變換隻能得到一個頻譜，做小波變換卻可以得到一個時頻譜！

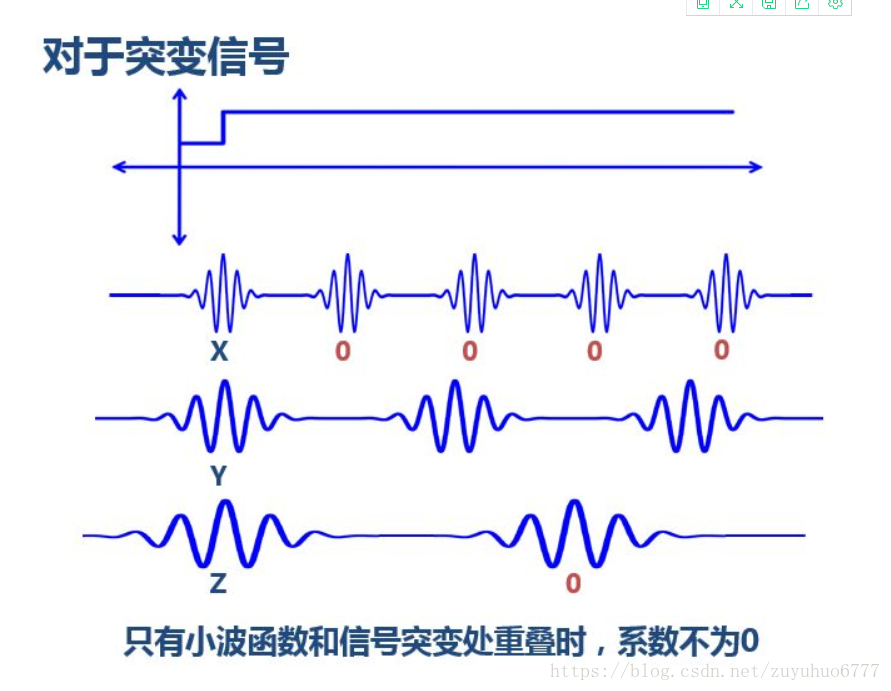
小波還有一些好處，比如，我們知道對於突變訊號，傅立葉變換存在吉布斯效應，我們用無限長的三角函式怎麼也擬合不好突變訊號：

然而衰減的小波就不一樣了：

以上，就是小波的意義。

不足之處請大家多留言

知識原理補充：

一些問題的回答：
1. 關於海森堡不確定性原理
不確定性原理，或者叫測不準原理，最早出自量子力學，意為在微觀世界，粒子的位置與動量不可同時被確定。但是這個原理並不侷限於量子力學，有很多物理量都有這樣的特徵，比如能量和時間、角動量和角度。體現在訊號領域就是時域和頻域。不過更準確一點的表述應該是：一個訊號不能在時空域和頻域上同時過於集中；一個函式時域越“窄”，它經傅立葉變換的頻域後就越“寬”。
如果有興趣深入研究一下的話，這個原理其實非常耐人尋味。訊號處理中的一些新理論在根本上也和它有所相連，比如壓縮感知。如果你剝開它複雜的數學描述，最後會發現它在本質上能實現其實和不確定性原理密切相關。而且大家不覺得這樣一些矛盾的東西在哲學意義上也很奇妙嗎？


2. 關於正交化
什麼是正交化？為什麼說小波能實現正交化是優勢?
簡單說，如果採用正交基，變換域係數會沒有冗餘資訊，變換前後的訊號能量相等，等於是用最少的資料表達最大的資訊量，利於數值壓縮等領域。JPEG2000壓縮就是用正交小波變換。
比如典型的正交基：二維笛卡爾座標系的（1,0）、（0,1），用它們表達一個訊號顯然非常高效，計算簡單。而如果用三個互成120°的向量表達，則會有資訊冗餘，有重複表達。
但是並不意味著正交一定優於不正交。比如如果是做影象增強，有時候反而希望能有一些冗餘資訊，更利於對噪聲的抑制和對某些特徵的增強。

3. 關於瞬時頻率
　　原問題：圖中時刻點對應一頻率值，一個時刻點只有一個訊號值，又怎麼能得到他的頻率呢？
　　很好的問題。如文中所說，絕對意義的瞬時頻率其實是不存在的。單看一個時刻點的一個訊號值，當然得不到它的頻率。我們只不過是用很短的一段訊號的頻率作為該時刻的頻率，所以我們得到的只是時間解析度有限的近似分析結果。這一想法在STFT上體現得很明顯。小波用衰減的基函式去測定訊號的瞬時頻率，思想也類似。（不過到了Hilbert變換，思路就不一樣了，以後有機會細講）

4. 關於小波變換的不足
這要看和誰比了。
A.作為影象處理方法，和多尺度幾何分析方法（超小波）比：
對於影象這種二維訊號的話，二維小波變換隻能沿2個方向進行，對影象中點的資訊表達還可以，但是對線就比較差。而影象中最重要的資訊恰是那些邊緣線，這時候ridgelet（脊波）, curvelet（曲波）等多尺度幾何分析方法就更有優勢了。
B. 作為時頻分析方法，和希爾伯特-黃變換（HHT）比：
相比於HHT等時頻分析方法，小波依然沒脫離海森堡測不準原理的束縛，某種尺度下，不能在時間和頻率上同時具有很高的精度；以及小波是非適應性的，基函式選定了就不改了。