我們知道，兩個 N 位數字的整數的乘法，如果使用常規的演算法，時間複雜度是 O(N²)。然而，使用快速傅立葉變換，時間複雜度可以降低到 O(N logN loglogN)。

假設我們要計算以下兩個 N 位數字的乘積：

a = (a_N-1a_N-2...a₁a₀)₁₀ = a_N-1x10^N-1 + a_N-2x10^N-2 + ... + a₁x10¹ + a₀x10⁰

b = (b_N-1b_N-2...b₁b₀)₁₀ = b_N-1x10^N-1 + b_N-2x10^N-2 + ... + b₁x10¹ + b₀x10⁰

將上面兩個式子相乘，得到以下公式 (共 2N - 1 項)：

c = a x b = c_2N-2x10^2N-2

非常容易驗證，上式中的 c_k ( 0 ≤ k ≤ 2N-2 ) 滿足以下公式：

c_k = a₀xb_k + a₁xb_k-1 + ... + a_k-2xb₂ + a_k-1xb₁
      + a_kxb₀ + a_k+1xb_-1 + ... + a_N-2xb_-(N-2-k) + a_N-1xb_-(N-1-k)

上式共有 N 項，a_i 和 b_j 的下標 i 和 j 滿足 i + j = k。若不滿足 0 ≤ i, j ≤ N-1 時，則令 a_i = b_j = 0。

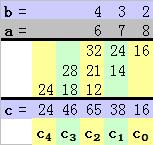
我們以兩個 3 ( N = 3 ) 位數 a = 678 和 b = 432 的乘積來說明以上過程吧。

a = (678)₁₀ = 6x10² + 7x10¹ + 8x10⁰

b = (432)₁₀ = 4x10² + 3x10¹ + 2x10⁰

由此： 

c₀ = a₀xb₀ + a₁xb_-1 + a₂xb_-2 = 8x2 + 7x0 + 6x0 = 16 + 0 + 0 = 16

c₁ = a₀xb₁ + a₁xb₀ + a₂xb_-1 = 8x3 + 7x2 + 6x0 = 24 + 14 + 0 = 38

c₂ = a₀xb₂ + a₁xb₁ + a₂xb₀ = 8x4 + 7x3 +6x2 = 32 + 21 + 12 = 65

c₃ = a₀xb₃ + a₁xb₂ + a₂xb₁ = 8x0 + 7x4 + 6x3 = 0 + 28 + 18 = 46

c₄ = a₀xb₄ + a₁xb₃ + a₂xb₂ = 8x0 + 7x0 + 6x4 = 0 + 0 + 24 = 24

最後：

c = a x b = 10⁴xc₄ + 10³xc₃ + 10²xc₂ + 10¹xc₁ + 10⁰xc₀
   = 10000x24 + 1000x46 + 100x65 + 10x38 + 1x16
   = 292896

如果按以上方法計算大整數的乘法，時間複雜度是 O(N²)。

但是，我們注意到，向量 {c_k} 是向量 {a_i} 和向量 {b_j} 的卷積。根據卷積定理，向量卷積的離散傅立葉變換是向量離散傅立葉變換的乘積。於是，我們可以按照以下步驟來計算大整數乘法：

對於複數向量 { x_N-1, ..., x₁, x₀ }，離散傅立葉變換公式為：

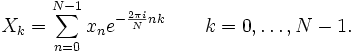
離散傅立葉逆變換公式為：

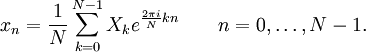
注意到離散傅立葉逆變換除了指數的符號相反以及結果需要乘以歸一化因子 1/N 外，與離散傅立葉變換是相同的。所以計算離散傅立葉變換的程式稍做修改也可以用於計算逆變換。

在我們的例子中，乘積 c = 292896，共 6 位數字，N 需要擴充套件到 2³ = 8。那麼，向量 {a_i} 和向量 {b_j} 如下所示：

{ a₇, a₆, a₅, a₄, a₃, a₂, a₁, a₀ } = { 0, 0, 0, 0, 0, 6, 7, 8 }

{ b₇, b₆, b₅, b₄, b₃, b₂, b₁, b₀ } = { 0, 0, 0, 0, 0, 4, 3, 2 }

為了求出以上向量的離散傅立葉變換，我們令

ω = e^-2πi/N = e^-2πi/8 = e^-πi/4 = cos(-π/4) + i sin(-π/4) = √2 / 2 - i √2 / 2 ≈ 0.7-0.7i

為了方便計算，我們預先求出 ω 的各次方，如下：

注意到當 n > 2 時，a_n = 0，於是： 

A₀ = a₀xω^0x0 + a₁xω^1x0 + a₂xω^2x0 = 8xω⁰ + 7xω⁰ + 6xω⁰ = 8x1 + 7x1 + 6x1 = 21

A₁ = a₀xω^0x1 + a₁xω^1x1 + a₂xω^2x1 = 8xω⁰ + 7xω¹ + 6xω² ≈ 8x1 + 7x(0.7 - 0.7i) + 6x(-i) = 12.9-10.9i

A₂ = a₀xω^0x2 + a₁xω^1x2 + a₂xω^2x2 = 8xω⁰ + 7xω² + 6xω⁴ = 8x1 + 7x(-i) + 6x(-1) = 2-7i

A₃ = a₀xω^0x3 + a₁xω^1x3 + a₂xω^2x3 = 8xω⁰ + 7xω³ + 6xω⁶ ≈ 8x1 + 7x(-0.7 - 0.7i) + 6xi = 3.1+1.1i

A₄ = a₀xω^0x4 + a₁xω^1x4 + a₂xω^2x4 = 8xω⁰ + 7xω⁴ + 6xω⁸ = 8x1 + 7x(-1) + 6x1 = 7

A₅ = a₀xω^0x5 + a₁xω^1x5 + a₂xω^2x5 = 8xω⁰ + 7xω⁵ + 6xω¹⁰ ≈ 8x1 + 7x(-0.7 + 0.7i) + 6x(-i) = 3.1-1.1i

A₆ = a₀xω^0x6 + a₁xω^1x6 + a₂xω^2x6 = 8xω⁰ + 7xω⁶ + 6xω¹² = 8x1 + 7xi + 6x(-1) = 2+7i

A₇ = a₀xω^0x7 + a₁xω^1x7 + a₂xω^2x7 = 8xω⁰ + 7xω⁷ + 6xω¹⁴ ≈ 8x1 + 7x(0.7 + 0.7i) + 6xi = 12.9+10.9i

同樣，當 n > 2 時，b_n = 0，於是： 

B₀ = b₀xω^0x0 + b₁xω^1x0 + b₂xω^2x0 = 2xω⁰ + 3xω⁰ + 4xω⁰ = 2x1 + 3x1 + 4x1 = 9

B₁ = b₀xω^0x1 + b₁xω^1x1 + b₂xω^2x1 = 2xω⁰ + 3xω¹ + 4xω² ≈ 2x1 + 3x(0.7 - 0.7i) + 4x(-i) = 4.1-6.1i

B₂ = b₀xω^0x2 + b₁xω^1x2 + b₂xω^2x2 = 2xω⁰ + 3xω² + 4xω⁴ = 2x1 + 3x(-i) + 4x(-1) = -2-3i

B₃ = b₀xω^0x3 + b₁xω^1x3 + b₂xω^2x3 = 2xω⁰ + 3xω³ + 4xω⁶ ≈ 2x1 + 3x(-0.7 - 0.7i) + 4xi = -0.1+1.9i

B₄ = b₀xω^0x4 + b₁xω^1x4 + b₂xω^2x4 = 2xω⁰ + 3xω⁴ + 4xω⁸ = 2x1 + 3x(-1) + 4x1 = 3

B₅ = b₀xω^0x5 + b₁xω^1x5 + b₂xω^2x5 = 2xω⁰ + 3xω⁵ + 4xω¹⁰ ≈ 2x1 + 3x(-0.7 + 0.7i) + 4x(-i) = -0.1-1.9i

B₆ = b₀xω^0x6 + b₁xω^1x6 + b₂xω^2x6 = 2xω⁰ + 3xω⁶ + 4xω¹² = 2x1 + 3xi + 4x(-1) = -2+3i

B₇ = b₀xω^0x7 + b₁xω^1x7 + b₂xω^2x7 = 2xω⁰ + 3xω⁷ + 4xω¹⁴ ≈ 2x1 + 3x(0.7 + 0.7i) + 4xi = 4.1+6.1i

這樣，向量 {a_i} 和向量 {b_j} 的離散傅立葉變換 {A_i} 和 {B_j} 如下所示：

{ A₇, A₆, A₅, A₄, A₃, A₂, A₁, A₀ } = { 12.9+10.9i, 2+7i, 3.1-1.1i, 7, 3.1+1.1i, 2-7i, 12.9-10.9i, 21 }

{ B₇, B₆, B₅, B₄, B₃, B₂, B₁, B₀ } = { 4.1+6.1i, -2+3i, -0.1-1.9i, 3, -0.1+1.9i, -2-3i, 4.1-6.1i, 9 }

現在，將她們逐項相乘得到向量 {C_k}，即 { C₇, C₆, C₅, C₄, C₃, C₂, C₁, C₀ }

= { -13.6+123.4i, -25-8i, -2.4-5.8i, 21, -2.4+5.8i, -25+8i, -13.6-123.4i, 189 }

為了求出向量 {C_k} 的離散傅立葉逆變換，我們令

ω = e^2πi/N = e^2πi/8 = e^πi/4 = cos(π/4) + i sin(π/4) = √2 / 2 + i √2 / 2 ≈ 0.7+0.7i

為了方便計算，我們預先求出 ω 的各次方(注意 ω^k+8 = ω^k)，如下：

於是： 

c₀ = (1/N) x ( C₀xω^0x0 + C₁xω^1x0 + C₂xω^2x0 + C₃xω^3x0 
                  + C₄xω^4x0 + C₅xω^5x0 + C₆xω^6x0 + C₇xω^7x0 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁰ + (-25+8i)xω⁰ + (-2.4+5.8i)xω⁰ 
                  + 21xω⁰ + (-2.4-5.8i)xω⁰ + (-25-8i)xω⁰ + (-13.6+123.4i)xω⁰ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x1 + (-25+8i)x1 + (-2.4+5.8i)x1 
                  + 21x1 + (-2.4-5.8i)x1 + (-25-8i)x1 + (-13.6+123.4i)x1 )
    = 0.125 x 128 = 16

c₁ = (1/N) x ( 8xc₁ = C₀xω^0x1 + C₁xω^1x1 + C₂xω^2x1 + C₃xω^3x1 
                  + C₄xω^4x1 + C₅xω^5x1 + C₆xω^6x1 + C₇xω^7x1 )
    = (1/8) x ( 189xω⁰ + ( -13.6-123.4i)xω¹ + (-25+8i)xω² + (-2.4+5.8i)xω³ 
                  + 21xω⁴ + (-2.4-5.8i)xω⁵ + (-25-8i)xω⁶ + (-13.6+123.4i)xω⁷ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(0.7+0.7i) + (-25+8i)x(i) + (-2.4+5.8i)x(-0.7+0.7i) 
                  + 21x(-1) + (-2.4-5.8i)x(-0.7-0.7i) + (-25-8i)x(-i) + (-13.6+123.4i)x(0.7-0.7i) )
    = 0.125 x 300.96 = 37.62 ≈ 38

c₂ = (1/N) x ( C₀xω^0x2 + C₁xω^1x2 + C₂xω^2x2 + C₃xω^3x2 
                  + C₄xω^4x2 + C₅xω^5x2 + C₆xω^6x2 + C₇xω^7x2 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω² + (-25+8i)xω⁴ + (-2.4+5.8i)xω⁶ 
                  + 21xω⁸ + (-2.4-5.8i)xω¹⁰ + (-25-8i)xω¹² + (-13.6+123.4i)xω¹⁴ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(i) + (-25+8i)x(-1) + (-2.4+5.8i)x(-i) 
                  + 21x1 + (-2.4-5.8i)x(i) + (-25-8i)x(-1) + (-13.6+123.4i)x(-i) )
    ≈ 0.125 x 518.4 = 64.8 ≈ 65

c₃ = (1/N) x ( C₀xω^0x3 + C₁xω^1x3 + C₂xω^2x3 + C₃xω^3x3 
                  + C₄xω^4x3 + C₅xω^5x3 + C₆xω^6x3 + C₇xω^7x3 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω³ + (-25+8i)xω⁶ + (-2.4+5.8i)xω⁹ 
                  + 21xω¹² + (-2.4-5.8i)xω¹⁵ + (-25-8i)xω¹⁸ + (-13.6+123.4i)xω²¹ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(-0.7+0.7i) + (-25+8i)x(-i) + (-2.4+5.8i)x(0.7+0.7i) 
                  + 21x(-1) + (-2.4-5.8i)x(0.7-0.7i) + (-25-8i)x(i) + (-13.6+123.4i)x(-0.7-0.7i) )
    = 0.125 x 364.32 = 45.54 ≈ 46

c₄ = (1/N) x ( C₀xω^0x4 + C₁xω^1x4 + C₂xω^2x4 + C₃xω^3x4 
                  + C₄xω^4x4 + C₅xω^5x4 + C₆xω^6x4 + C₇xω^7x4 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁴ + (-25+8i)xω⁸ + (-2.4+5.8i)xω¹² 
                  + 21xω¹⁶ + (-2.4-5.8i)xω²⁰ + (-25-8i)xω²⁴ + (-13.6+123.4i)xω²⁸ )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(-1) + (-25+8i)x1 + (-2.4+5.8i)x(-1) 
                  + 21x1 + (-2.4-5.8i)x(-1) + (-25-8i)x1 + (-13.6+123.4i)x(-1) )
    = 0.125 x 192 = 24

c₅ = (1/N) x ( C₀xω^0x5 + C₁xω^1x5 + C₂xω^2x5 + C₃xω^3x5 
                  + C₄xω^4x5 + C₅xω^5x5 + C₆xω^6x5 + C₇xω^7x5 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁵ + (-25+8i)xω¹⁰ + (-2.4+5.8i)xω¹⁵ 
                  + 21xω²⁰ + (-2.4-5.8i)xω²⁵ + (-25-8i)xω³⁰ + (-13.6+123.4i)xω³⁵ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(-0.7-0.7i) + (-25+8i)x(i) + (-2.4+5.8i)x(0.7-0.7i) 
                  + 21x(-1) + (-2.4-5.8i)x(0.7+0.7i) + (-25-8i)x(-i) + (-13.6+123.4i)x(-0.7+0.7i) )
    = 0.125 x 3.04 = 0.38 ≈ 0

c₆ = (1/N) x ( C₀xω^0x6 + C₁xω^1x6 + C₂xω^2x6 + C₃xω^3x6 
                  + C₄xω^4x6 + C₅xω^5x6 + C₆xω^6x6 + C₇xω^7x6 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁶ + (-25+8i)xω¹² + (-2.4+5.8i)xω¹⁸ 
                  + 21xω²⁴ + (-2.4-5.8i)xω³⁰ + (-25-8i)xω³⁶ + (-13.6+123.4i)xω⁴² )
    = 0.125 x ( 189x1 + (-13.6-123.4i)x(-i) + (-25+8i)x(-1) + (-2.4+5.8i)x(i) 
                  + 21x1 + (-2.4-5.8i)x(-i) + (-25-8i)x(-1) + (-13.6+123.4i)x(i) )
    = 0.125 x 1.6 = 0.2 ≈ 0

c₇ = (1/N) x ( C₀xω^0x7 + C₁xω^1x7 + C₂xω^2x7 + C₃xω^3x7 
                  + C₄xω^4x7 + C₅xω^5x7 + C₆xω^6x7 + C₇xω^7x7 )
    = (1/8) x ( 189xω⁰ + (-13.6-123.4i)xω⁷ + (-25+8i)xω¹⁴ + (-2.4+5.8i)xω²¹ 
                  + 21xω²⁸ + (-2.4-5.8i)xω³⁵ + (-25-8i)xω⁴² + (-13.6+123.4i)xω⁴⁹ )
    ≈ 0.125 x ( 189x1 + (-13.6-123.4i)x(0.7-0.7i) + (-25+8i)x(-i) + (-2.4+5.8i)x(-0.7-0.7i) 
                  + 21x(-1) + (-2.4-5.8i)x(-0.7+0.7i) + (-25-8i)x(i) + (-13.6+123.4i)x(0.7+0.7i) )
    = 0.125 x 3.68 = 0.46 ≈ 0 

這樣，我們就使用離散傅立葉變換和逆變換計算出了向量 {a_i} 和向量 {b_j} 的卷積向量 {c_k}，如下所示：

{ c₇, c₆, c₅, c₄, c₃, c₂, c₁, c₀ } = { 0, 0, 0, 0, 24, 46, 65, 38, 16 }

這和我們在前面直接使用向量 {a_i} 和向量 {b_j} 來計算卷積的結果是一樣的。

但是，這個演算法的時間複雜度還是 O(N²)。我們繞了這麼一大圈，不是白費勁了嗎？

現在就到了關鍵時刻，關鍵在於：直接進行離散傅立葉變換的計算複雜度是 O(N²)。快速傅立葉變換可以計算出與直接計算相同的結果，但只需要 O(N logN) 的計算複雜度。 N logN 和 N² 之間的差別是巨大的。例如，當 N = 10⁶ 時，在一個每秒運算百萬次的計算機上，粗略地說，它們之間就是佔用 30 秒 CPU 時間和兩星期 CPU 時間的差別。

快速傅立葉變換的要點如下：一個界長為 N 的離散傅立葉變換可以重新寫成兩個界長各為 N/2 的離散傅立葉變換之和。其中一個變換由原來 N 個點中的偶數點構成，另一個變換由奇數點構成。這個過程可以遞迴地進行下去，直到我們將全部資料細分為界長為 1 的變換。什麼是界長為 1 的傅立葉變換呢？它正是把一個輸入值複製成它的一個輸出值的恆等運算。要實現以上演算法，最容易的情況是原始的 N 為 2 的整冪次項，如果資料集的界長不是 2 的冪次時，則可添上一些零值，直到 2 的下一冪次。在這個演算法中，每遞迴一次需 N 階運算，共需要 log N 次遞迴，所以快速傅立葉變換演算法的時間複雜度是 O(N logN)。

由於快速傅立葉變換是採用了浮點運算，因此我們需要足夠的精度，以使在出現舍入誤差時，結果中每個組成部分的準確整數值仍是可辨認的。長度為 N 的 B 進位制數可產生大到 B²N 階的卷積分量。我們知道，雙精度浮點數的尾數是 53 個二進位，所以：

2 x log₂B + log₂N + 幾個 x log₂log₂N < 53

上式中左邊最後一項是為了快速傅立葉變換的舍入誤差。

所以，為了能夠計算儘量大的整數，一般 B 不會取得太大。在計算機程式中經常使用 256 進位制進行運算。但是如果經常需要將計算結果和十進位制互相轉換，則往往使用 100 進位制進行運算。

關於快速傅立葉變換以及卷積定理的更深入的知識，請參閱文末的參考文獻。這一篇隨筆主要是講述相關的原理，在下一篇隨筆中，我將給出一個使用快速傅立葉變換進行任意精度的算術運算的 C# 程式。

順便說一句，我在準備正文的例題的時候，是使用 google 計算器來進行復雜的複數運算的。發現她非常好用。以計算 c₂ 為例， 只要將要計算的表示式複製到 goole 搜尋欄，然後按回車，就能得到計算結果：