背景

給出讀《艾伯特貝葉斯思維：統計建模的Python學習法.pdf》的時候，寫的程式碼，以面向過程的方式給出。
本章彩彈問題，求似然度的時候，假設已知隱藏點時，射手等概率從各個角度射擊。

程式碼

匯入常見模組

# %load "E:\桌面space\臨時資料\python\個人自定義模組\ImportFile.py"
# Standard Scientific Import
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib as mpl
from matplotlib import pyplot as
 
 plt
from matplotlib.pyplot import plot as plot
import sklearn
import seaborn as sns
import sys
import patsy

# 個人程式碼測試路徑
sys.path.append(r"C:\Users\Administrator\PycharmProjects\QY_TS_Quant")
from QY_plot import *

plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文字型設定-黑體
plt.rcParams['axes.unicode_minus'
 
] = False  # 解決儲存影象是負號'-'顯示為方塊的問題
sns.set(font='SimHei',font_scale=1.25,style="ticks",rc={"xtick.major.size": 3, "ytick.major.size": 3})# 解決Seaborn中文顯示問題

# Jupyter 預設設定
%matplotlib inline
%config InlineBackend.figure_format="retina"
%config InlineBackend.rc = {"figure.figsize": (7.5,4.5)}

# 多列輸出
from
 
 IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

中間函式

from functools import reduce
import operator

# 假設在alpha,beta的射手，隨機等概率可以往各個方向設計
def StrafingSpeed(alpha, beta, x):
    return (np.square(beta)+np.square(alpha-x))/beta

def normlize(x):
    return x/np.sum(x)

def MakePmf(alpha, beta, w=30):
    pmf = list(map(lambda v:1./ StrafingSpeed(alpha, beta, v), np.arange(w+1)))
    return normlize(pmf)

def likehood(AX, AY, x, w=30):
    AZS = reduce(operator.add, map(lambda v:1./StrafingSpeed(AX, AY, v),np.arange(w+1)))
    AZ =  1./StrafingSpeed(AX, AY, x)
    return  AZ/AZS

# 圍場寬30， 長50
w = 30
h = 50

# 寬邊 中彈位置
x = [15, 16, 18, 21]

假定射擊點時，牆上各點被擊打概率

alpha = 10
beta = 10
plt.plot(MakePmf(alpha, beta))

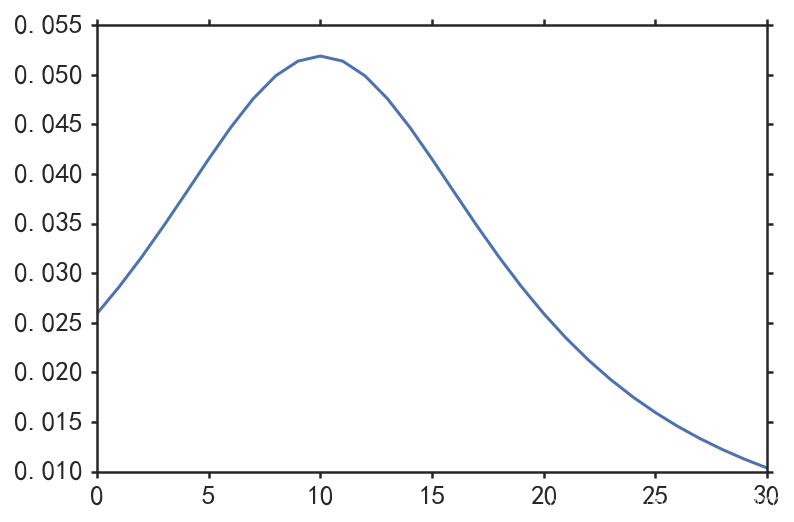
二維射擊點分佈

def update(AP,x):
    if not np.isscalar(x):
        for xi in x:
            AP = update(AP, xi)
    else:
        AZ = likehood(AX, AY, x)
        AP = AP*AZ
        AP /= AP.sum()
    return AP

X = np.arange(w+1)
Y = np.arange(1, h+1)
AX, AY = np.meshgrid(X, Y)

AP = np.ones_like(AX)
AP = update(AP, x)

plt.contour(AX,AY,AP,80)
plt.colorbar()

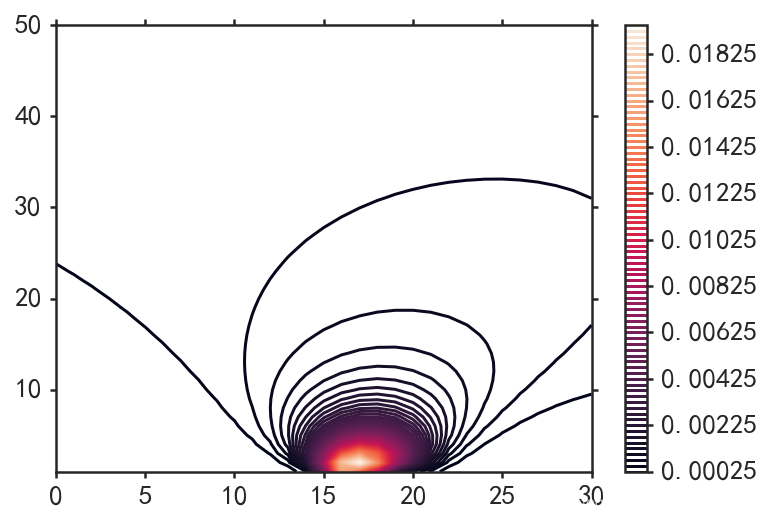
邊緣分佈

fig, axes = plt.subplots(1, 2, figsize=(18, 6))
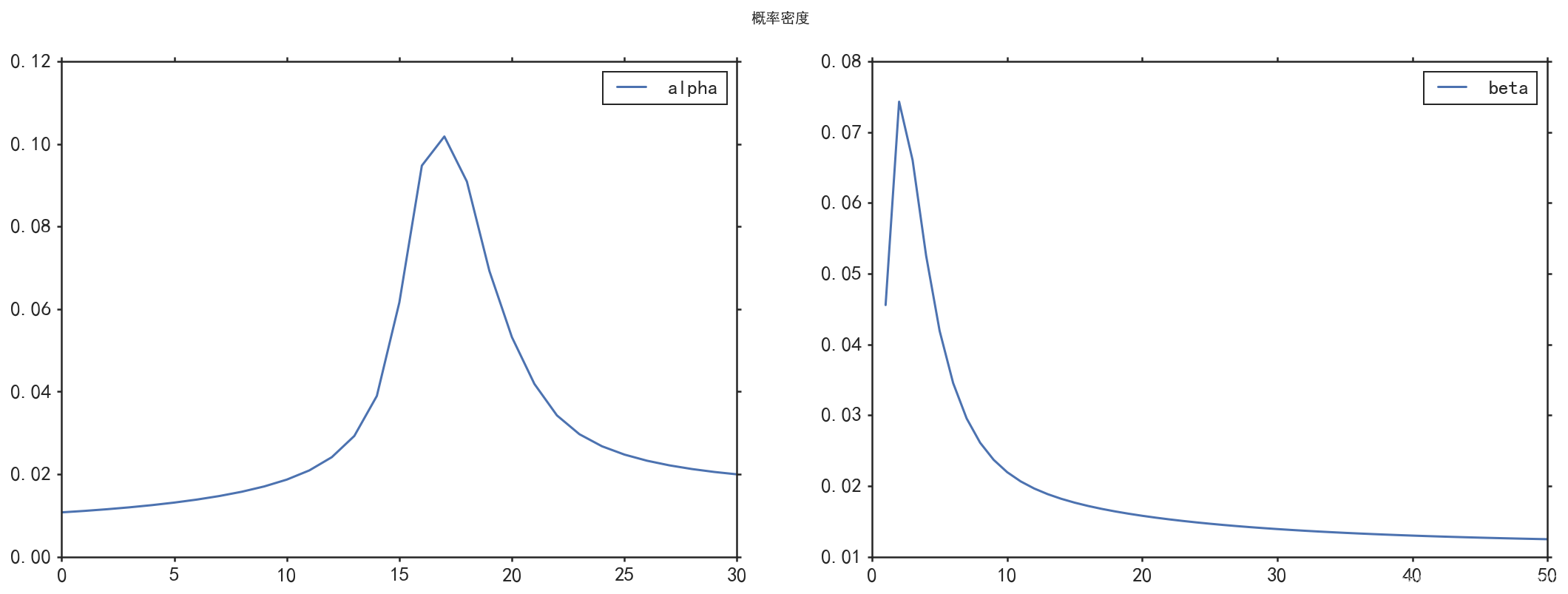
axes[0].plot(AX[0], AP.sum(axis=0), label="alpha")
axes[1].plot(AY[:,0], AP.sum(axis=1), label="beta")
axes[0].legend();
axes[1].legend();
plt.suptitle("概率密度");

fig, axes = plt.subplots(1, 2, figsize=(18, 6))
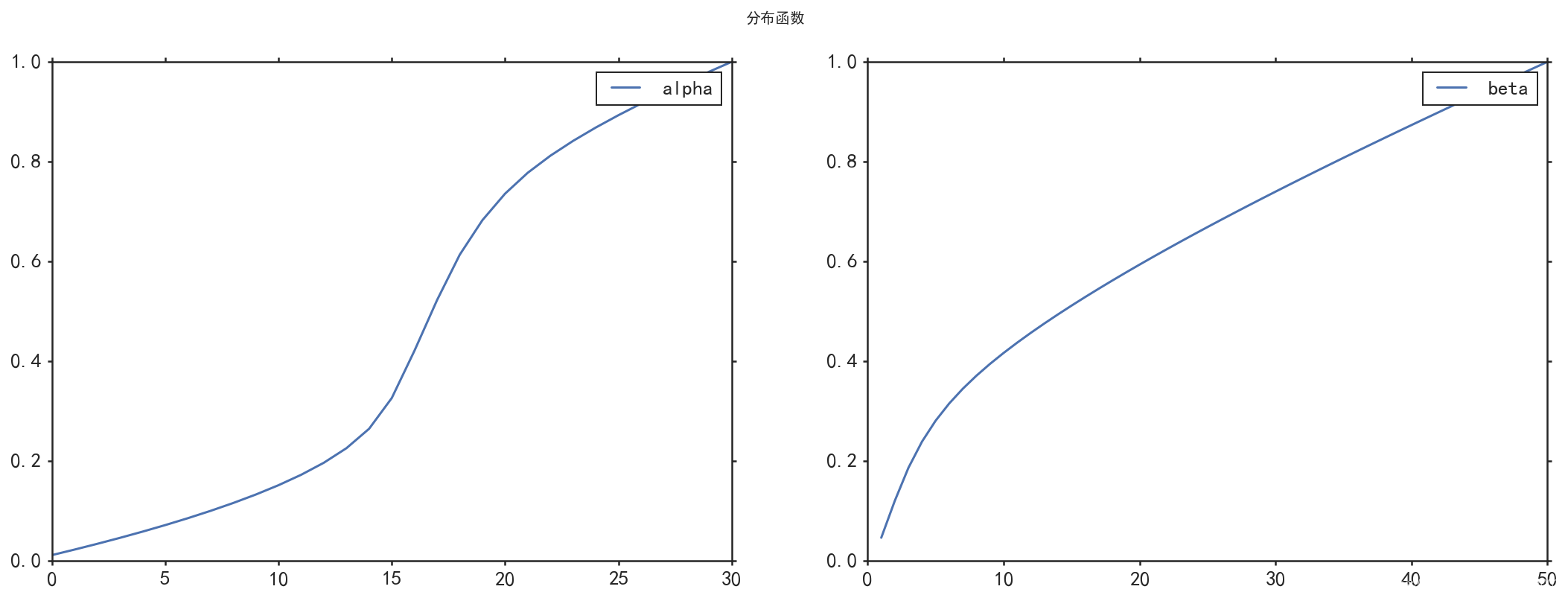
axes[0].plot(AX[0], AP.sum(axis=0).cumsum(), label="alpha")
axes[1].plot(AY[:,0],AP.sum(axis=1).cumsum(), label="beta")
axes[0].legend();
axes[1].legend();
plt.suptitle("分佈函式");

def confintv(cdf, p):
    t = []
    flag = 0
    for i,v in enumerate(cdf):
        if flag==0:
            if v>=0.5-p/2:
                t.append(i)
                flag=1
        elif flag==1:
            if v>=0.5+p/2:
                t.append(i)
                break
    return t

# alpha的 50%置信區間
AX[0][confintv(AP.sum(axis=0).cumsum(), 0.5)]

array([14, 21])

# beta的50%置信區間
AY[:,1][confintv(AP.sum(axis=1).cumsum(), 0.5)]

array([ 5, 31])

置信區間

Acolor = np.zeros_like(AP)
s = np.argsort(AP.ravel())
for v in np.searchsorted(AP.flat[s].cumsum(),[0.25, 0.5, 0.75]):
    Acolor.flat[s[:v]] += 0.25

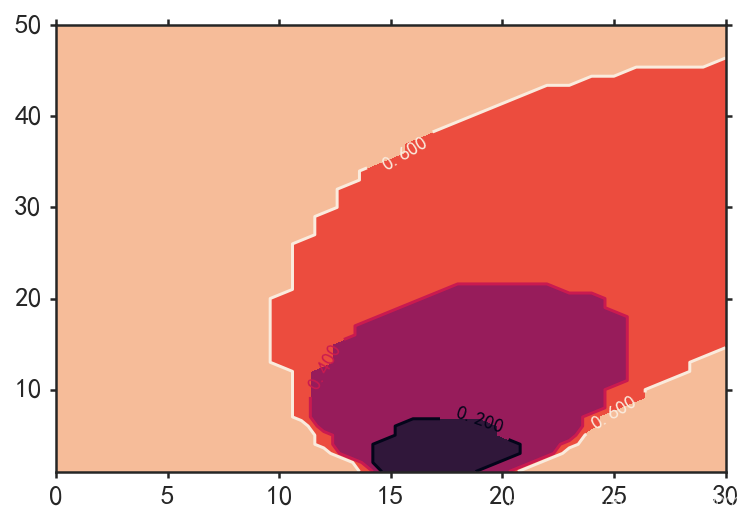
plt.imshow(Acolor, origin=True, aspect=0.5)

clf = plt.contour(AX, AY, Acolor,3);
plt.clabel(clf, fontsize=10);
plt.contourf(AX, AY, Acolor, 3);