禁忌搜尋演算法原理及實現

圖著色問題

對給定圖G=(V,E)的每個頂點著色,要求每個相鄰的頂點不同色，求最小需要的顏色數。

禁忌搜尋演算法

禁忌搜尋演算法，是一種區域性搜尋演算法，通過採用禁忌表，逃脫了區域性最優解，得到全域性最優解。禁忌搜尋演算法先針對問題初始化一個解決方案S，和目標值O。下一步在S鄰域中挑選可以使得目標值O最小的禁忌或者非禁忌移動。同時將本次移動記錄在禁忌表中，設定一個禁忌值tt，當迭代次數小於禁忌值時本次移動屬於禁忌移動，否則屬於非禁忌移動。演算法終止條件是求出解，或者達到設定的迭代次數。

演算法流程：
（1）生成初始解決方案S，計算衝突值f(S)
（2）初始化鄰接顏色表M,禁忌表T,歷史最佳衝突best_f
（3）判斷是否滿足終止條件不滿足繼續執行，滿足則停止
（4）構造S的鄰域，用N(S)表示
（5）計算領域N(S)中所有一步移動的△值
（6）找到具有最小△值的最佳禁忌或者非禁忌移動
（7）如果滿足願望條件則執行最佳禁忌移動，否則執行最佳非禁忌移動
（8）更新解決方案，衝突f，歷史最佳衝突best_f，禁忌表，鄰接顏色表
（9）執行步驟（3）

鄰接顏色表M：NXK的陣列,N為結點數，K為顏色數。M[i][j]表示i結點的鄰接節點中,具有j顏色的節點的數目。
每次移動，衝突增量△f = M[i][j]-M[old_i][old_j]，等於新顏色的M[i][j]減去舊顏色的M[i][j]，鄰接顏色表
i的所有鄰接節點，新顏色j列的值+1，舊顏色old_j列的值-1。

禁忌表T：NXK的陣列,NXK的陣列,N為結點數，K為顏色數。初始為0,每次迭代從i的舊顏色old_j移動到新顏色j,T[i][j]
的值設定為一個禁忌值tt(如前所述)。

領域N(S): S的下一次移動所有的可能結果，對於本問題就是依次移動每個節點至除了當前顏色的每個顏色，如果當前顏色與鄰接節點的顏色衝突已經為0則不需要移動。

願望條件：最佳禁忌移動的目標值小於歷史最佳衝突best_f且小於當前非禁忌移動的值,則可接受禁忌移動的值，否則接受非禁忌移動的值。

程式碼實現

TabuSearch(){ 
    int u, vi, vj, iter = 0;
    Initialization() ;//初始化
    while( iter < MaxIter) {
        FindMove(u,vi,vj,delt) ;//找到最佳禁忌移動或者非禁忌移動
        MakeMove(u,vi,vj,delt) ;//更新相應值
    }
}

備註：單純的禁忌搜尋演算法求解圖著色，可不用設定其迭代次數，一直執行即可。

核心程式碼實現

1. findmove實現

   //找最佳禁忌或者非禁忌移動
   void findmove() {
       delt = 10000;//初始為最大整數
       int tmp;//臨時變數
       int tabu_delt = 10000;
       int count = 0, tabu_count = 0;
       int A = best_f - f;
       int c_color;//當前結點顏色
       int *h_color;//鄰接顏色錶行首指標
       int *h_tabu;//禁忌錶行首指標
       int c_color_table;//當前結點顏色表的值
       for (int i = 0; i<N; i++) {//11.3
           c_color = sol[i];//6.1%
           h_color = adj_color_table[i];
           c_color_table = h_color[c_color];
           if (h_color[c_color] > 0) {//17.6
               h_tabu = tabutenure[i];
               for (int j = 0; j < K; j++) {
                   if (c_color != j) {//cpu流水線
                       //非禁忌移動
                       tmp = h_color[j] - c_color_table;
                       if (h_tabu[j] <= iter) {//22.6
                           if (tmp <= delt) {//分支預判懲罰 6.0
                               if (tmp < delt) {
                                   count = 0;
                                   delt = tmp;
                               }
                               count++;
                               equ_delt[count - 1][0] = i;
                               equ_delt[count - 1][1] = j;
                           }
                       }else {//禁忌移動
                           if (tmp <= tabu_delt) {//6.0
                               if (tmp < tabu_delt) {
                                   tabu_delt = tmp;
                                   tabu_count = 0;
                               }
                               tabu_count++;
                               equ_tabudelt[tabu_count - 1][0] = i;
                               equ_tabudelt[tabu_count - 1][1] = j;
                           }
                       }
                   }
               }
           }
       }
       tmp = 0;
       if (tabu_delt<A && tabu_delt < delt) {
           delt = tabu_delt;
           tmp = rand() % tabu_count;//相等delt隨機選擇
           node = equ_tabudelt[tmp][0];
           color = equ_tabudelt[tmp][1];
       }
       else {
           tmp = rand() % count;//相等delt隨機選擇
           node = equ_delt[tmp][0];
           color = equ_delt[tmp][1];
       }
   }

2. makemove實現

   //更新值
   void makemove() {
       f = delt + f;//更新衝突值
       if (f < best_f) best_f = f ;//更新歷史最好衝突
       int old_color = sol[node];
       sol[node] = color;
       tabutenure[node][old_color] = iter + f + rand() % 10 + 1;//更新禁忌表
       int *h_graph = g[node];
       int num_edge = v_edge[node];
       int tmp;
       for (int i = 0; i<num_edge; i++) {//更新鄰接顏色表
           tmp = h_graph[i];
           adj_color_table[tmp][old_color]--;
           adj_color_table[tmp][color]++;
       }
   }

3. 結果
   

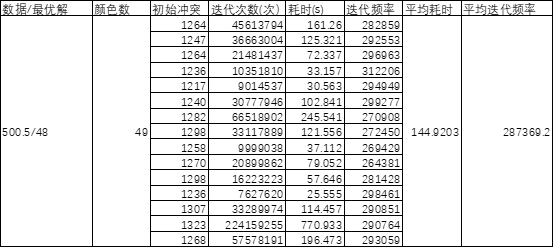
禁忌演算法注意點

1. 歷史最優衝突best_f，取最小值，取其他值，可能使得收斂過慢。
2. 採用迭代次數與禁忌表比較，而不是每次迭代禁忌表非零值-1，然後比較與0的大小，增加了時間複雜度。

實現過程中做的優化

程式碼優化

1. 採用鄰接表
   鄰接表的時間複雜度比二維陣列的時間複雜度更低，如果邊少，會低很多。
   程式碼中做法是：採用二維陣列，並另使用一個一維陣列存放每行的長度。
2. 採用陣列
   vector耗時是陣列的5.6倍（對於此問題而言）。
   struct耗時也比陣列多。
3. 二維陣列按行訪問
   c++中二維陣列按行儲存，為了提高cpu Cache命中率，實現按行訪問。
   程式碼中的具體做法是：外重迴圈取二維陣列行首地址，內重迴圈使用行首地址訪問。
4. 提高分支預判命中
   迴圈內部，讓分支條件儘可能為真，或為假，有規律，讓cpu可命中。
   程式碼中的具體做法是：if(c_color!=j)這是大部分為真的情況。

編譯優化

1. g++ tabu.cpp O2 -o tabu,採用O2（程式碼速度)最快編譯。vs->屬性->c/c++->優化->O2。

工具優化

1. 採用vs的profile查詢耗時的程式碼，分析優化

實踐中用到的知識

1. 隨機數

   srand((unsigned)time(NULL));
   rand();

   time(NULL)返回64bit時間，rand()超int範圍，採用debug x64後正常。
   真實原因是指標訪問錯誤，滯後的原因。
   rand()在每次被呼叫的時候，它會檢視：
   1） 如果使用者在此之前呼叫過srand(seed)，給seed指定了一個值，那麼它會自動呼叫srand(seed)一次來初始化它的起始值。
   2） 如果使用者在此之前沒有呼叫過srand(seed)，它會自動呼叫srand(1)一次。
   注：秒的隨機不夠精確，程式執行很快秒隨機在1000個迴圈之內可能不會改變，使用毫秒clock()，微妙隨機。

2. 按行讀取檔案，並按空格分割

   /* 
   @in, src: 待分割的字串 
   @in, delim: 分隔符字串 
   @in_out, dest: 儲存分割後的每個字串 
   */  
   void split(const string& src, const string& delim, vector<string>& dest)  
   {  
       string str = src;  
       string::size_type start = 0, index;  
       string substr;  
       index = str.find(delim, start);    //在str中查詢(起始：start) delim的任意字元的第一次出現的位置  
       while(index != string::npos)  
       {  
           substr = str.substr(start, index-start);  
           dest.push_back(substr);
           start = index + 1;  
           index = str.find(delim, start);    //在str中查詢(起始：index) 第一個不屬於delim的字元出現的位置  
       }  
       substr = str.substr(start, index);  
       dest.push_back(substr);
   } 
   int main(){
       ifstream infile("test.txt", ios::in);  
       vector<string> results;  
       string delim(" ");  
       string textline;  
       if(infile.good())  
       {  
           while(!infile.fail())  
           {  
               getline(infile, textline);  
               split(textline, delim, results); 
           }  
       }  
       infile.close();
       return 0;
   }

3. C++內建型別最大值巨集定義

   
   #include<climits>
   
   INT_MAX

4. 0xC0000005: 讀取位置 0x0000000000000000 時發生訪問衝突
   0xC0000005: 讀取位置 0x0000000000000040 時發生訪問衝突
   訪問衝突原因：
   指標越界：將指標資料依次輸出，模擬訪問

5. 記憶體分配異常處理
   try{}catch(const bad_alloc &e){}

6. Critical error detected c0000374
   有時候因為malloc / new / whatever檢測到堆損壞，往往這個損壞在程式中以前就已經發生了，但是崩潰一直延遲到下一次呼叫new / malloc。
   錯誤很可能是陣列越界，指標地址損壞等引起。可通過模擬訪問輸出每個地址的資料，進行檢查。

7. 程式已退出,返回值為 0 (0x0)
   引用標頭檔案時多加一個#include “stdlib.h ”
   在return 0前加一個system(“pause”);

8. 輸出到檔案的資料過多時
   為避免影響程式時間，可採用取樣輸出，比如隔10000輸出一次

9. 二維陣列申請釋放
   指標：
   申請：

   int **array = new int*[N];
   for(int i = 0;i < N;i++)
       array[i] = new int[K];

   釋放：

   for(int i = 0;i < N;i++)
       delete []array[i]
   delete []array;

   vector:

   vector<vector<int>> v;
   v = new vector(M,vector<int>());

10. a debugger is attached to but not configured to debug this unhandled exception. to debug this exception detach the current debugger in Visual Studio
    如果Visual Studio配置為只調試託管的異常，並且您獲得的異常是本地的，則可能會出現此警告。 轉到您的專案的屬性，除錯選項，並將偵錯程式型別從託管只更改為混合（託管和本機）。

11. cpu cache對程式效能的影響
    由於計算機的記憶體是一維的，多維陣列的元素應排成線性序列後存入儲存器。陣列一般不做插入和刪除操作，即結構中元素個數和元素間的關係不變。
    所以採用順序儲存方法表示陣列。c/c++二維陣列按行優先儲存，所以儘量讓二維陣列按行訪問優先，避免跨行訪問，提高cpu cache命中率。
    以矩陣乘法為例，瞭解cpu cache對程式效能的影響
    cpu cache對程式效能的影響
    如何用 Cache 在 C++ 程式中進行系統級優化（二）
    如何用 Cache 在 C++ 程式中進行系統級優化（一）

12. 程式碼裡寫很多if會影響效率嗎?
    現代處理器先執行if條件，如果不對在回滾切換到其他分支，所以儘量讓if語句,要麼一直true,要麼一直false，有規律可循
    程式碼裡寫很多if會影響效率嗎?
    分支預判代價
    快速和慢速的 if 語句：現代處理器的分支預測

13. “/Ox”和“/RTC1”命令列選項不相容 或者 ml.exe 退出
    “/Ox”和“/RTC1”命令列選項不相容,將/RTC1改為預設值，或者禁用優化

14. cpu cache介紹
    L1,L2,L33級別快取：
    L1一個核兩個一個指令一個數據
    L2一個cpu一個
    L3同一卡槽的cpu共享一個
    計算機體系結構2—-快取cache

15. java/c++誰快
    java雖然解釋執行，但可針對特定處理器優化。下面兩篇文章說java快。
    但相同程式開了O2優化後，C++比java快。
    Java VS C/C++ 執行速度的對比
    c++vsjava

16. 安裝g++編譯器嘗試g++O3級別優化
    編譯執行：

    g++ tabu.cpp -O3 -o tabu
    tabu.exe

參考

1. 華科，呂志鵬教授，啟發式優化