詳解反向傳播演算法(上)
目錄:
1 用計算圖來解釋幾種求導方法:
1.1 計算圖
1.2 兩種求導模式:前向模式求導( forward-mode differentiation) 反向模式求導(reverse-mode differentiation)
1.3 反向求導模式(反向傳播演算法)的重要性
反向傳播演算法(Backpropagation)已經是神經網路模型進行學習的標配。但是有很多問題值得思考一下:
反向傳播演算法的作用是什麼? 神經網路模型的學習演算法一般是SGD。SGD需要用到損失函式C關於各個權重引數的偏導數。一個模型的引數w,b是非常多的,故而需要反向傳播演算法快速計算。也就是說反向傳播演算法是一種計算偏導數的方法。
為什麼要提出反向傳播演算法? 在反向傳播演算法提出之前人們應該想到了使用SGD學習模型,也想到了一些辦法求解網路模型的偏導數,但這些演算法求解效率比較低,所以提出反向傳播演算法來更高效的計算偏導數。(那時的網路模型還比較淺只有2-3層,引數少。估計即便不適用反向傳播這種高效的演算法也能很好的學習。一旦有人想使用更深的網路自然會遇到這個偏導數無法高效計算的問題,提出反向傳播也就勢在必行了)
反向傳播怎麼樣實現高效計算偏導數的? 請先回顧一下當初我們學習微積分時是如何計算偏導數的? (鏈式法則,具體看下面)
1 用計算圖來解釋幾種求導方法:
1.1 計算圖
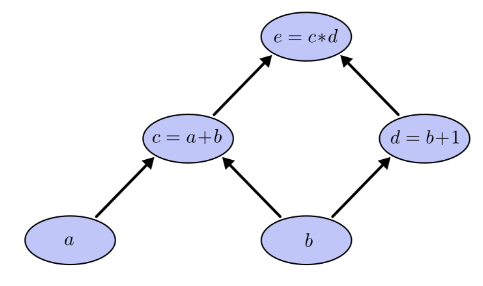
式子 可以用如下計算圖表達:
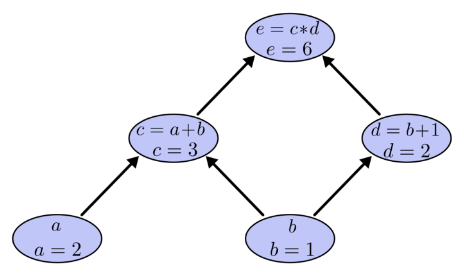
令a=2,b=1則有:
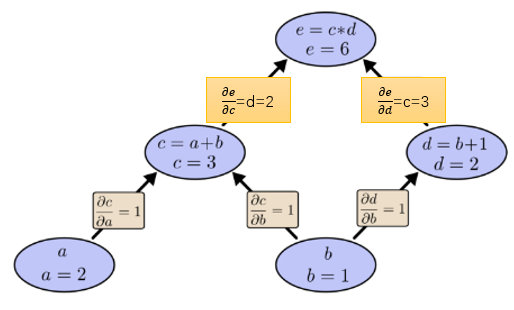
如何在計算圖上表達“求導”呢? 導數的含義是 因變數隨自變數的變化率,例如 表示當x變化1個單位,y會變化3個單位。 微積分中已經學過:加法求導法則是 乘法求導法則是 。 我們在計算圖的邊上表示導數或偏導數: 如下圖
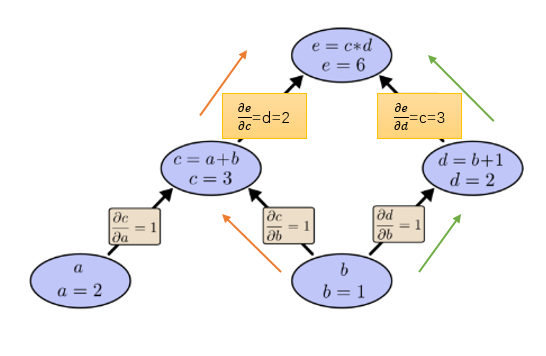
那麼 如何求呢? 告訴我們1個單位的b變化會引起1個單位的c變換,告訴我們 1 個單位的c變化會引起2個單位的e變化。所以 嗎? 答案必然是錯誤。因為這樣做只考慮到了下圖橙色的路徑,所有的路徑都要考慮:
所以上面的求導方法總結為一句話就是: 路徑上所有邊相乘,所有路徑相加。不過這裡需要補充一條很有用的合併策略:
例如:下面的計算圖若要計算就會有9條路徑:
如果計算圖再複雜一些,層數再多一些,路徑數量就會呈指數爆炸性增長。但是如果採用合併策略: 就不會出現這種問題。這種策略不是 對每一條路徑都求和,而是 “合併同類路徑”,“分階段求解”。先求X對Y的總影響 再求Y對Z的總影響 最後綜合在一起。
1.2 兩種求導模式:前向模式求導( forward-mode differentiation) 反向模式求導(reverse-mode differentiation)
上面提到的求導方法都是前向模式求導( forward-mode differentiation) :從前向後。先求X對Y的總影響 再乘以Y對Z的總影響 。
另一種,反向模式求導(reverse-mode differentiation) 則是從後向前。先求Y對Z的影響再乘以X對Y的影響。
前向求導模式追蹤一個輸入如何影響每一個節點(對每一個節點進行 操作)反向求導模式追蹤每一個節點如何影響一個輸出(對每一個節點進行 操作)。
1.3 反向求導模式(反向傳播演算法)的重要性:
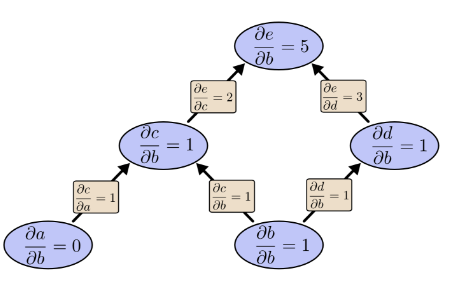
讓我們再次考慮前面的例子:
如果用前向求導模式:關於b向前求導一次
如果用反向求導模式:向後求導前向求導模式只得到了關於輸入b的偏導 ,還需要再次求解關於輸入a的偏導 (運算2遍)。而反向求導一次運算就得到了e對兩個輸入a,b的偏導 (運算1遍)。上面的比較只看到了2倍的加速。但如果有1億個輸入1個輸出,意味著前向求導需要操作1億遍才得到所有關於輸入的偏導,而反向求導則只需一次運算,1億倍的加速。
當我們訓練神經網路時,把“損失“ 看作 ”權重引數“ 的函式,需要計算”損失“關於每一個”權重引數“的偏導數(然後用梯度下降法學習)。 神經網路的權重引數可以是百萬甚至過億級別。因此 反向求導模式(反向傳播演算法)可以極大的加速學習。
參考:
相關推薦
詳解反向傳播演算法(上)
目錄: 1 用計算圖來解釋幾種求導方法: 1.1 計算圖 1.2 兩種求導模式:前向模式求導( forward-mode differentiation) 反向模式求導(reverse-mode differentiation) 1.3 反向求導模式(反向傳播演算法)的重要性 反向傳播演算法(Backp
深度學習 --- BP演算法詳解(誤差反向傳播演算法)
本節開始深度學習的第一個演算法BP演算法,本打算第一個演算法為單層感知器,但是感覺太簡單了,不懂得找本書看看就會了,這裡簡要的介紹一下單層感知器: 圖中可以看到,單層感知器很簡單,其實本質上他就是線性分類器,和機器學習中的多元線性迴歸的表示式差不多,因此它具有多元線性迴歸的優點和缺點。
乾貨 | 深度學習之CNN反向傳播演算法詳解
微信公眾號 關鍵字全網搜尋最新排名 【機器學習演算法】:排名第一 【機器學習】:排名第一 【Python】:排名第三 【演算法】:排名第四 前言 在卷積神經網路(CNN)前向傳播演算法(乾貨 | 深度學習之卷積神經網路(CNN)的前向傳播演算法詳解)中對CNN的前向傳播演算法做了總結,基於CNN前向傳播演
反向傳播演算法詳解
作者:Great Learning Team 神經網路 什麼是反向傳播? 反向傳播是如何工作的? 損失函式 為什麼我們需要反向傳播? 前饋網路 反向傳播的型別 案例研究 在典型的程式設計中,我們輸入資料,執行處理邏輯並接收輸出。 如果輸出資料可以某種方式影響處理邏輯怎麼辦? 那就是反向傳播演算法。 它
吳恩達機器學習(第十章)---神經網路的反向傳播演算法
一、簡介 我們在執行梯度下降的時候,需要求得J(θ)的導數,反向傳播演算法就是求該導數的方法。正向傳播,是從輸入層從左向右傳播至輸出層;反向傳播就是從輸出層,算出誤差從右向左逐層計算誤差,注意:第一層不計算,因為第一層是輸入層,沒有誤差。 二、如何計算 設為第l層,第j個的誤差。
吳恩達機器學習 - 神經網路的反向傳播演算法 吳恩達機器學習 - 神經網路的反向傳播演算法
原 吳恩達機器學習 - 神經網路的反向傳播演算法 2018年06月21日 20:59:35 離殤灬孤狼 閱讀數:373
BP反向傳播演算法
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script> #該程式碼加入MathJax引擎,用以顯
(轉載)深度學習基礎(3)——神經網路和反向傳播演算法
原文地址:https://www.zybuluo.com/hanbingtao/note/476663 轉載在此的目的是自己做個筆記,日後好複習,如侵權請聯絡我!! 在上一篇文章中,我們已經掌握了機器學習的基本套路,對模型、目標函式、優化演算法這些概念有了一定程度的理解,而且已經會訓練單個的感知器或者
深度學習 --- BP演算法詳解(BP演算法的優化)
上一節我們詳細分析了BP網路的權值調整空間的特點,深入分析了權值空間存在的兩個問題即平坦區和區域性最優值,也詳細探討了出現的原因,本節將根據上一節分析的原因進行改進BP演算法,本節先對BP存在的缺點進行全面的總結,然後給出解決方法和思路,好,下面正式開始本節的內容: BP演算法可以完成非線性
通俗理解神經網路BP反向傳播演算法
轉載自 通俗理解神經網路BP反向傳播演算法 通俗理解神經網路BP反向傳播演算法 在學習深度學習相關知識,無疑都是從神經網路開始入手,在神經網路對引數的學習演算法bp演算法,接觸了很多次,每一次查詢資料學習,都有著似懂非懂的感覺,這次趁著思路比較清楚,也為了能夠讓一些像
最小生成樹圖文詳解(Prim演算法)
最小生成樹 就像幾個村莊都不相通, 要修路, 怎麼修, 這個花的錢最少, 這種最優選擇就是最小生成樹 設G = (V, E)是無向連通圖(V是結點集, E是邊集),相對於村莊例子,V就是那些村莊的集合,E就是村莊之間路的集合
反向傳播演算法(BP演算法)
BP演算法(即反向傳播演算法),適合於多層神經元網路的一種學習演算法,它建立在梯度下降法的基礎上。BP網路的輸入輸出關係實質上是一種對映關係:一個n輸入m輸出的BP神經網路所完成的功能是從n維歐氏空間向m維歐氏空間中一有限域的連續對映,這一對映具有高度非線性。它的資訊處理能力來源於簡單非線性函式的多
deeplearning.ai-正向和反向傳播演算法公式
【正向和反向傳播】 【梯度下降i法】 【邏輯迴歸代價函式】 【實現神經網路的步驟】 【淺層神經網路例子】 import numpy as np def sigmoid(x): """ Compute the sigmoid of x
全連線神經網路的反向傳播演算法(BP)
一、預熱篇 參考連結:http://colah.github.io/posts/2015-08-Backprop/ 要理解的主要點:路徑上所有邊相乘,所有路徑相加 反向傳播演算法(Backpropagation)已經是神經網路模型進行學習的標配。但是有很多問題值得思考一下: 反向傳播
Plupload上傳外掛詳解,多例項上傳
我們來看一個比較全的 Plupload Demo <!DOCTYPE html> <html> <head> <meta charset="U
神經網路中反向傳播演算法(BP)
神經網路中反向傳播演算法(BP) 本文只是對BP演算法中的一些內容進行一些解釋,所以並不是嚴格的推導,因為我在推導的過程中遇見很多東西,當時不知道為什麼要這樣,所以本文只是對BP演算法中一些東西做點自己的合理性解釋,也便於自己理解。 要想看懂本文,要懂什麼是神經網路,對前向傳播以
吳恩達機器學習筆記-神經網路的代價函式和反向傳播演算法
代價函式 在神經網路中,我們需要定義一些新的引數來表示代價函式。 L = total number of layers in the network $s_l$ = number of units (not counting bias unit) in layer
Android系列教程之七:EditText使用詳解-包含很多教程上看不到的功能演示
Android系列教程目錄: 一:新建HelloEditText工程 新建一個Hello world詳細步驟可以參見 建立設定如下: Project name:HelloEditTextBuild Target :android 2.2Application name
神經網路的反向傳播演算法中矩陣的求導方法(矩陣求導總結)
前言 神經網路的精髓就是反向傳播演算法,其中涉及到一些矩陣的求導運算,只有掌握了與矩陣相關的求導法則才能真正理解神經網路. 與矩陣有關的求導主要分為兩類: 標量 f 對 矩陣 W的導數 (其結果是和W同緯度的矩陣,也就是f對W逐元素求導排成與W尺寸相同的矩陣
BP神經網路反向傳播演算法一步一步例項推導(Backpropagation Example)
1. loss 函式的優化 籠統來講: 設計loss函式是為了衡量網路輸出值和理想值之間的差距,儘管網路的直接輸出並不顯式的包含權重因子,但是輸出是同權重因子直接相關的,因此仍然可以將loss函式視作在權重因子空間中的一個函式。 可以將loss 記為E(w),這裡為

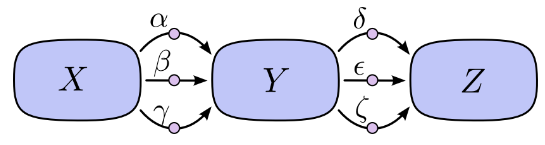 如果計算圖再複雜一些,層數再多一些,路徑數量就會呈指數爆炸性增長。但是如果採用合併策略:
如果計算圖再複雜一些,層數再多一些,路徑數量就會呈指數爆炸性增長。但是如果採用合併策略: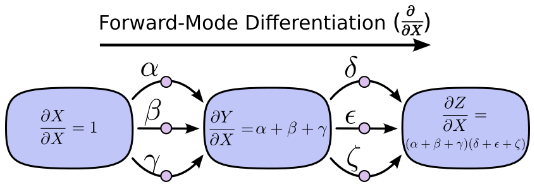
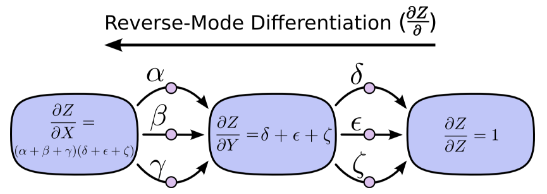
 如果用反向求導模式:向後求導
如果用反向求導模式:向後求導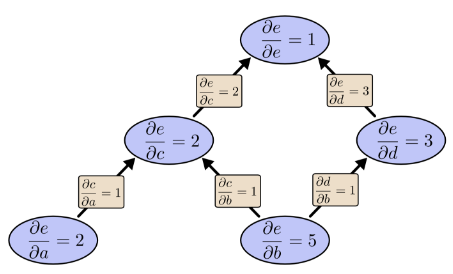 前向求導模式只得到了關於輸入b的偏導
前向求導模式只得到了關於輸入b的偏導