1. Google的DQN論文

Atari 2600是80年代風靡美國的遊戲機，總共包括49個獨立的遊戲，其中不乏我們熟悉的Breakout（打磚塊），Galaxy Invaders（小蜜蜂）等經典遊戲。Google演算法的輸入只有遊戲螢幕的影象和遊戲的得分，在沒有人為干預的情況下，電腦自己學會了遊戲的玩法，而且在29個遊戲中打破了人類玩家的記錄。

Google給出的深度絡架構圖如下：

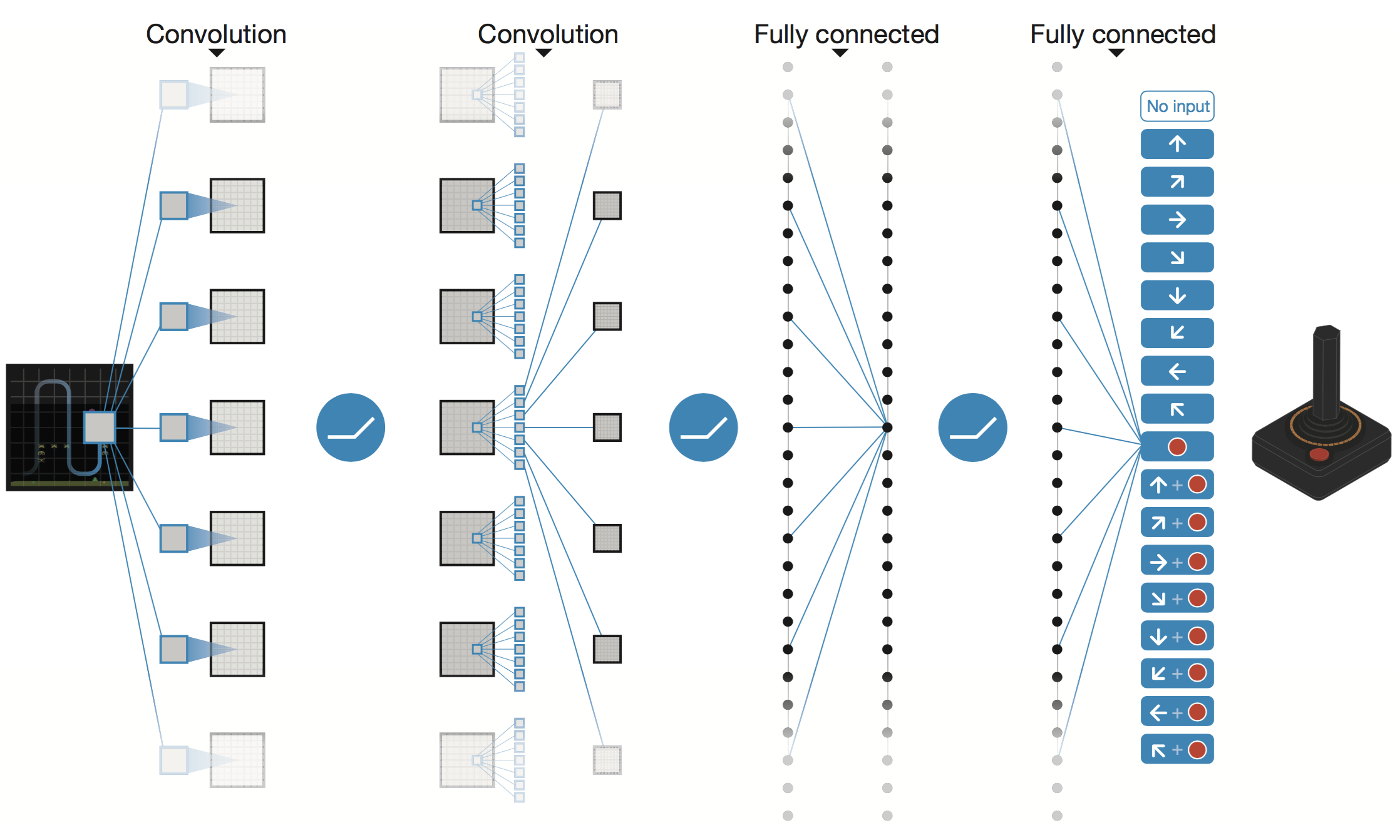
網路的左邊是輸入，右邊是輸出。 遊戲螢幕的影象先經過兩個卷積層（論文中寫的是三個），然後經過兩個全連線層， 最後對映到遊戲手柄所有可能的動作。各層之間使用ReLU啟用函式。

2. 強化學習(Q-Learning)

根據維基百科的描述，強化學習定義如下:
強化學習是機器學習中的一個領域，強調如何基於環境而行動，以取得最大化的預期利益。其靈感來源於心理學中的行為主義理論，即有機體如何在環境給予的獎勵或懲罰的刺激下，逐步形成對刺激的預期，產生能獲得最大利益的習慣性行為。

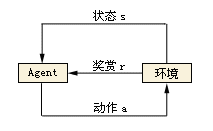
在強化學習的世界裡， 演算法稱之為Agent， 它與環境發生互動，Agent從環境中獲取狀態（state），並決定自己要做出的動作（action）.環境會根據自身的邏輯給Agent予以獎勵（reward）。獎勵有正向和反向之分。比如在遊戲中，每擊中一個敵人就是正向的獎勵，掉血或者遊戲結束就是反向的獎勵。

2.1. 馬爾可夫決策過程

現在的問題是，你如何公式化一個強化學習問題，然後進行推導呢？最常見的方法是通過馬爾可夫決策過程。

假設你是一個代理，身處某個環境中（例如《打磚塊》遊戲）。這個環境處於某個特定的狀態（例如，牌子的位置、球的位置與方向，每個磚塊存在與否）。人工智慧可以可以在這個環境中做出某些特定的動作（例如，向左或向右移動拍子）。

這些行為有時候會帶來獎勵（分數的上升）。行為改變環境，並帶來新的狀態，代理可以再執行另一個動作。你選擇這些動作的規則叫做策略。通常來說，環境是隨機的，這意味著下一狀態也或多或少是隨機的（例如，當你漏掉了球，發射一個新的時候，它會去往隨機的方向）。

狀態與動作的集合，加上改變狀態的規則，組成了一個馬爾可夫決策過程。這個過程（例如一個遊戲）中的一個情節（episode）形成了狀態、動作與獎勵的有限序列。

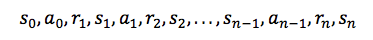
其中 si 表示狀態，ai 表示動作，ri+1 代表了執行這個動作後獲得的獎勵。情節以最終的狀態 sn 結束（例如，「Game Over」畫面）。一個馬爾可夫決策過程基於馬爾可夫假設（Markov assumption），即下一狀態 si+1 的概率取決於現在的狀態 si 和動作 ai，而不是之前的狀態與動作。

2.2. 折扣未來獎勵（Discounted Future Reward）

為了長期表現良好，我們不僅需要考慮即時獎勵，還有我們將得到的未來獎勵。我們該如何做呢？

對於給定的馬爾可夫決策過程的一次執行，我們可以容易地計算一個情節的總獎勵：

鑑於此，時間點 t 的總未來回報可以表達為：

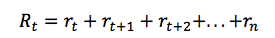
但是由於我們的環境是隨機的，我們永遠無法確定如果我們在下一個相同的動作之後能否得到一樣的獎勵。時間愈往前，分歧也愈多。因此，這時候就要利用折扣未來獎勵來代替：

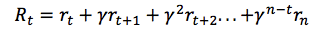
在這裡 γ 是數值在0與1之間的貼現因子——獎勵在距離我們越遠的未來，我們便考慮的越少。我們很容易看到，折扣未來獎勵在時間步驟 t 的數值可以根據在時間步驟 t+1 的相同方式表示：

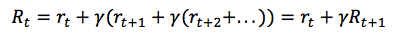
如果我們將貼現因子定義為 γ=0，那麼我們的策略將會過於短淺，即完全基於即時獎勵。如果我們希望平衡即時與未來獎勵，那麼貼現因子應該近似於 γ=0.9。如果我們的環境是確定的，相同的動作總是導致相同的獎勵，那麼我們可以將貼現因子定義為 γ=1。

一個代理做出的好的策略應該是去選擇一個能夠最大化（折扣後）未來獎勵的動作。

2.3. Q-Learning演算法描述：

演算法中的 α 是指學習率，其控制前一個 Q 值和新提出的 Q 值之間被考慮到的差異程度。尤其是，當 α=1 時，兩個 Q[s,a] 互相抵消，結果剛好和貝爾曼方程一樣。
我們用來更新 Q[s,a] 的只是一個近似，而且在早期階段的學習中它完全可能是錯誤的。但是隨著每一次迭代，該近似會越來越準確；而且我們還發現如果我們執行這種更新足夠長時間，那麼 Q 函式就將收斂並能代表真實的 Q 值。

3. 卷積神經網路(CNN)

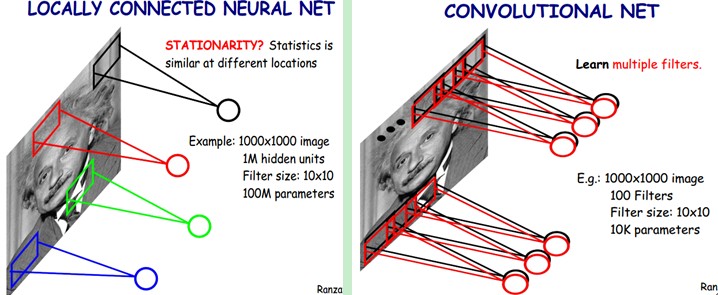
在影象處理中，往往把影象表示為畫素的向量，比如一個1000×1000的影象，可以表示為一個1000000的向量。在上一節中提到的神經網路中，如果隱含層數目與輸入層一樣，即也是1000000時，那麼輸入層到隱含層的引數資料為1000000×1000000=10^12，這樣就太多了，基本沒法訓練。所以影象處理要想練成神經網路大法，必先減少引數加快速度。

3.1. 區域性感知

卷積神經網路有兩種神器可以降低引數數目，第一種神器叫做區域性感知野。一般認為人對外界的認知是從區域性到全域性的，而影象的空間聯絡也是區域性的畫素聯絡較為緊密，而距離較遠的畫素相關性則較弱。

因而，每個神經元其實沒有必要對全域性影象進行感知，只需要對區域性進行感知，然後在更高層將區域性的資訊綜合起來就得到了全域性的資訊。網路部分連通的思想，也是受啟發於生物學裡面的視覺系統結構。視覺皮層的神經元就是區域性接受資訊的（即這些神經元只響應某些特定區域的刺激）。如下圖所示：左圖為全連線，右圖為區域性連線。

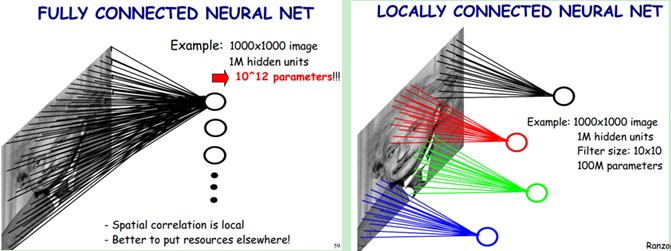
在上右圖中，假如每個神經元只和10×10個畫素值相連，那麼權值資料為1000000×100個引數，減少為原來的萬分之一。而那10×10個畫素值對應的10×10個引數，其實就相當於卷積操作。

3.2. 引數共享

但其實這樣的話引數仍然過多，那麼就啟動第二級神器，即權值共享。在上面的區域性連線中，每個神經元都對應100個引數，一共1000000個神經元，如果這1000000個神經元的100個引數都是相等的，那麼引數數目就變為100了。

怎麼理解權值共享呢？我們可以這100個引數（也就是卷積操作）看成是提取特徵的方式，該方式與位置無關。這其中隱含的原理則是：影象的一部分的統計特性與其他部分是一樣的。這也意味著我們在這一部分學習的特徵也能用在另一部分上，所以對於這個影象上的所有位置，我們都能使用同樣的學習特徵。

更直觀一些，當從一個大尺寸影象中隨機選取一小塊，比如說 8x8 作為樣本，並且從這個小塊樣本中學習到了一些特徵，這時我們可以把從這個 8x8 樣本中學習到的特徵作為探測器，應用到這個影象的任意地方中去。特別是，我們可以用從 8x8 樣本中所學習到的特徵跟原本的大尺寸影象作卷積，從而對這個大尺寸影象上的任一位置獲得一個不同特徵的啟用值。

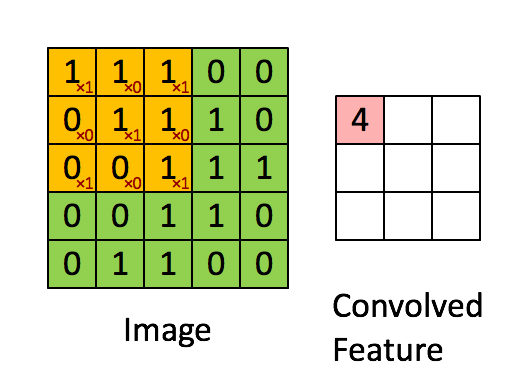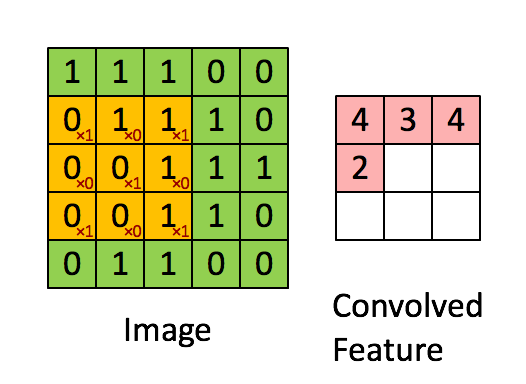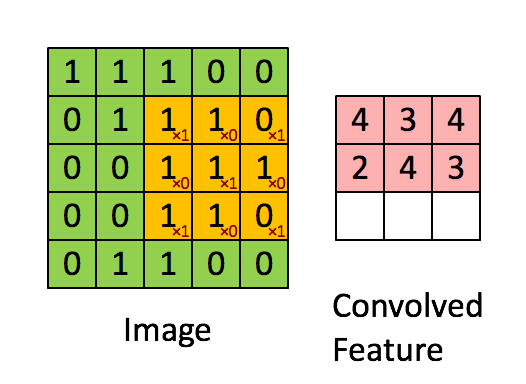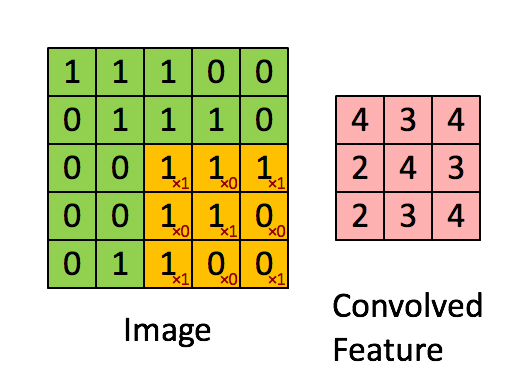
如下圖所示，展示了一個3×3的卷積核在5×5的影象上做卷積的過程。每個卷積都是一種特徵提取方式，就像一個篩子，將影象中符合條件（啟用值越大越符合條件）的部分篩選出來。

3.3. 多卷積核

上面所述只有100個引數時，表明只有1個10×10的卷積核，顯然，特徵提取是不充分的，我們可以新增多個卷積核，比如32個卷積核，可以學習32種特徵。在有多個卷積核時，如下圖所示：

上圖右，不同顏色表明不同的卷積核。每個卷積核都會將影象生成為另一幅影象。比如兩個卷積核就可以將生成兩幅影象，這兩幅影象可以看做是一張影象的不同的通道。如下圖所示，下圖有個小錯誤，即將w1改為w0，w2改為w1即可。下文中仍以w1和w2稱呼它們。

下圖展示了在四個通道上的卷積操作，有兩個卷積核，生成兩個通道。其中需要注意的是，四個通道上每個通道對應一個卷積核，先將w2忽略，只看w1，那麼在w1的某位置（i,j）處的值，是由四個通道上（i,j）處的卷積結果相加然後再取啟用函式值得到的。

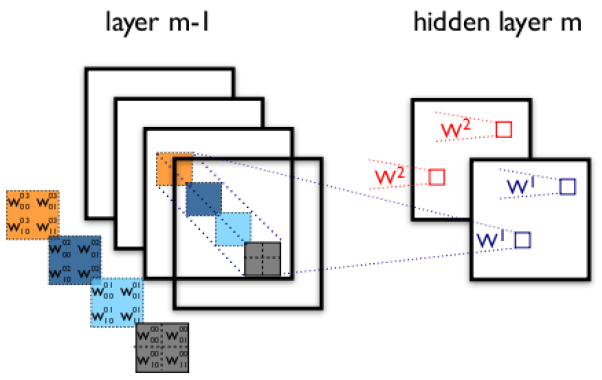
所以，在上圖由4個通道卷積得到2個通道的過程中，引數的數目為4×2×2×2個，其中4表示4個通道，第一個2表示生成2個通道，最後的2×2表示卷積核大小。

3.4. Down-pooling

在通過卷積獲得了特徵 (features) 之後，下一步我們希望利用這些特徵去做分類。理論上講，人們可以用所有提取得到的特徵去訓練分類器，例如 softmax 分類器，但這樣做面臨計算量的挑戰。

例如：對於一個 96X96 畫素的影象，假設我們已經學習得到了400個定義在8X8輸入上的特徵，每一個特徵和影象卷積都會得到一個 (96 − 8 + 1) × (96 − 8 + 1) = 7921 維的卷積特徵，由於有 400 個特徵，所以每個樣例 (example) 都會得到一個 7921 × 400 = 3,168,400 維的卷積特徵向量。學習一個擁有超過 3 百萬特徵輸入的分類器十分不便，並且容易出現過擬合 (over-fitting)。

為了解決這個問題，首先回憶一下，我們之所以決定使用卷積後的特徵是因為影象具有一種“靜態性”的屬性，這也就意味著在一個影象區域有用的特徵極有可能在另一個區域同樣適用。

因此，為了描述大的影象，一個很自然的想法就是對不同位置的特徵進行聚合統計，例如，人們可以計算影象一個區域上的某個特定特徵的平均值 (或最大值)。這些概要統計特徵不僅具有低得多的維度 (相比使用所有提取得到的特徵)，同時還會改善結果(不容易過擬合)。這種聚合的操作就叫做池化 (pooling)，有時也稱為平均池化或者最大池化 (取決於計算池化的方法)。

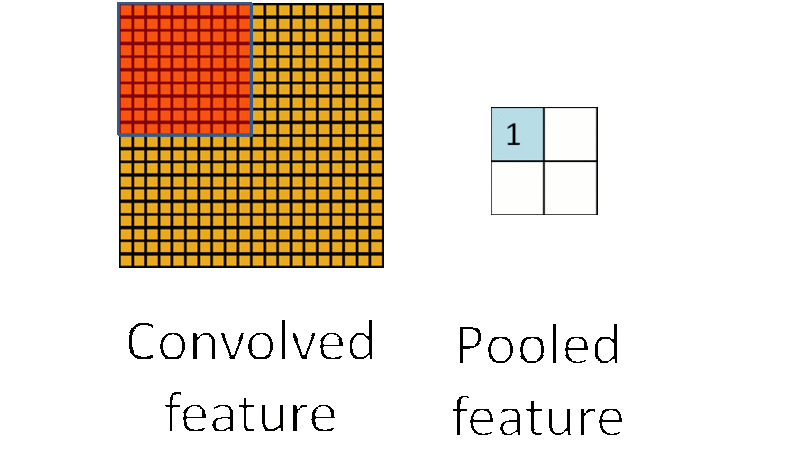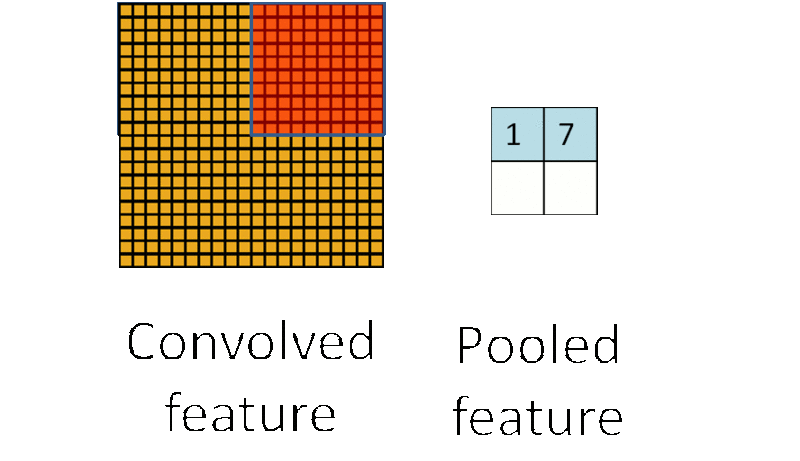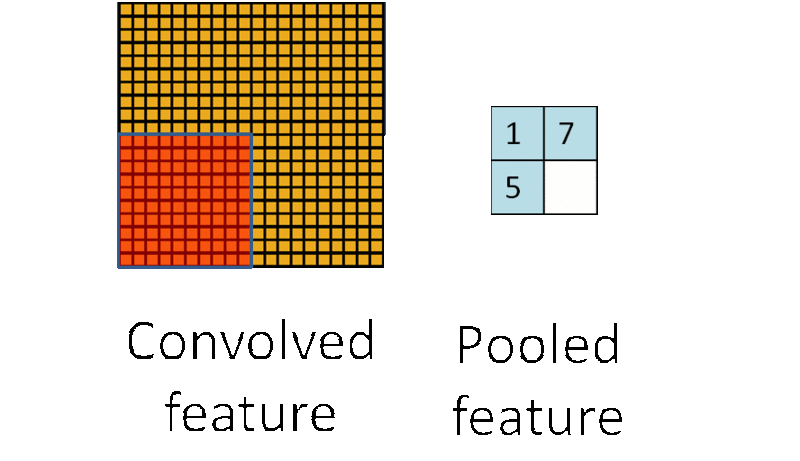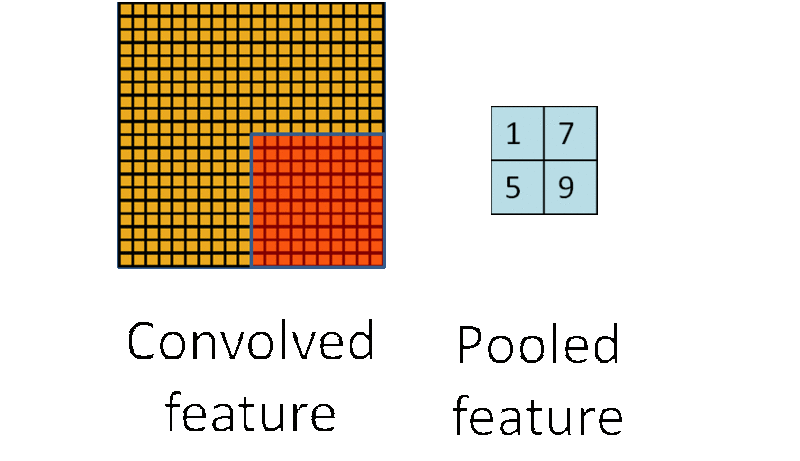
3.5. 多層卷積

在實際應用中，往往使用多層卷積，然後再使用全連線層進行訓練，多層卷積的目的是一層卷積學到的特徵往往是區域性的，層數越高，學到的特徵就越全域性化。

4. DQN演算法描述

單純的Q-Learning演算法使用表來儲存狀態，一個1000×1000影象的畫素狀態數基本接近與無窮，故有了CNN+Q-Learning 即DQN演算法，演算法描述如下：

5. 使用DQN訓練“接磚塊”遊戲

深度學習的開源類庫比較多，比較著名的有tensorlow、caffe等。此處我們使用Tensorflow來訓練遊戲“接磚塊”。

遊戲截圖如下：

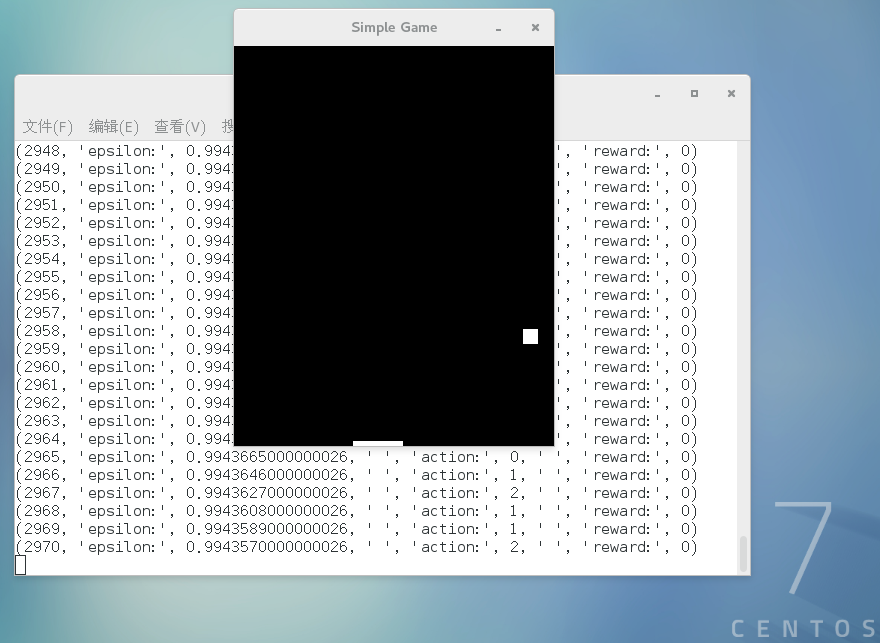
通過點選滑鼠左鍵、右鍵控制滑塊的左右移動來接住小球，如果球碰到底面，則遊戲結束

主要python程式碼如下(遊戲本身的程式碼省略，此處主要關注演算法程式碼)：

#Game的定義類，此處Game是什麼不重要，只要提供執行Action的方法，獲取當前遊戲區域畫素的方法即可
class Game(object):
    def __init__(self):  #Game初始化
    # action是MOVE_STAY、MOVE_LEFT、MOVE_RIGHT  
    # ai控制棒子左右移動；返回遊戲介面畫素數和對應的獎勵。(畫素->獎勵->強化棒子往獎勵高的方向移動)  
    def step(self, action):

# learning_rate
LEARNING_RATE = 0.99
# 跟新梯度
INITIAL_EPSILON = 1.0
FINAL_EPSILON = 0.05
# 測試觀測次數
EXPLORE = 500000 
OBSERVE = 500
# 記憶經驗大小
REPLAY_MEMORY = 500000
# 每次訓練取出的記錄數
BATCH = 100
# 輸出層神經元數。代表3種操作-MOVE_STAY:[1, 0, 0]  MOVE_LEFT:[0, 1, 0]  MOVE_RIGHT:[0, 0, 1] 
output = 3  # MOVE_STAY:[1, 0, 0]  MOVE_LEFT:[0, 1, 0]  MOVE_RIGHT:[0, 0, 1]
input_image = tf.placeholder("float", [None, 80, 100, 4])  # 遊戲畫素
action = tf.placeholder("float", [None, output])     # 操作
#定義CNN-卷積神經網路
def convolutional_neural_network(input_image):
    weights = {'w_conv1':tf.Variable(tf.zeros([8, 8, 4, 32])),
               'w_conv2':tf.Variable(tf.zeros([4, 4, 32, 64])),
               'w_conv3':tf.Variable(tf.zeros([3, 3, 64, 64])),
               'w_fc4':tf.Variable(tf.zeros([3456, 784])),
               'w_out':tf.Variable(tf.zeros([784, output]))}

    biases = {'b_conv1':tf.Variable(tf.zeros([32])),
              'b_conv2':tf.Variable(tf.zeros([64])),
              'b_conv3':tf.Variable(tf.zeros([64])),
              'b_fc4':tf.Variable(tf.zeros([784])),
              'b_out':tf.Variable(tf.zeros([output]))}

    conv1 = tf.nn.relu(tf.nn.conv2d(input_image, weights['w_conv1'], strides = [1, 4, 4, 1], padding = "VALID") + biases['b_conv1'])
    conv2 = tf.nn.relu(tf.nn.conv2d(conv1, weights['w_conv2'], strides = [1, 2, 2, 1], padding = "VALID") + biases['b_conv2'])
    conv3 = tf.nn.relu(tf.nn.conv2d(conv2, weights['w_conv3'], strides = [1, 1, 1, 1], padding = "VALID") + biases['b_conv3'])
    conv3_flat = tf.reshape(conv3, [-1, 3456])
    fc4 = tf.nn.relu(tf.matmul(conv3_flat, weights['w_fc4']) + biases['b_fc4'])

    output_layer = tf.matmul(fc4, weights['w_out']) + biases['b_out']
    return output_layer

#訓練神經網路
def train_neural_network(input_image):
    predict_action = convolutional_neural_network(input_image)

    argmax = tf.placeholder("float", [None, output])
    gt = tf.placeholder("float", [None])

    action = tf.reduce_sum(tf.mul(predict_action, argmax), reduction_indices = 1)
    cost = tf.reduce_mean(tf.square(action - gt))
    optimizer = tf.train.AdamOptimizer(1e-6).minimize(cost)

    game = Game()
    D = deque()

    _, image = game.step(MOVE_STAY)
    image = cv2.cvtColor(cv2.resize(image, (100, 80)), cv2.COLOR_BGR2GRAY)
    ret, image = cv2.threshold(image, 1, 255, cv2.THRESH_BINARY)
    input_image_data = np.stack((image, image, image, image), axis = 2)
    #print ("IMG2:%s" %input_image_data)

    with tf.Session() as sess:
        sess.run(tf.initialize_all_variables())

        saver = tf.train.Saver()

        n = 0
        epsilon = INITIAL_EPSILON
        while True:
            #print("InputImageData:", input_image_data)
            action_t = predict_action.eval(feed_dict = {input_image : [input_image_data]})[0]

            argmax_t = np.zeros([output], dtype=np.int)
            if(random.random() <= INITIAL_EPSILON):
                maxIndex = random.randrange(output)
            else:
                maxIndex = np.argmax(action_t)
            argmax_t[maxIndex] = 1
            if epsilon > FINAL_EPSILON:
                epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / EXPLORE

            reward, image = game.step(list(argmax_t))

            image = cv2.cvtColor(cv2.resize(image, (100, 80)), cv2.COLOR_BGR2GRAY)
            ret, image = cv2.threshold(image, 1, 255, cv2.THRESH_BINARY)
            image = np.reshape(image, (80, 100, 1))
            input_image_data1 = np.append(image, input_image_data[:, :, 0:3], axis = 2)

            D.append((input_image_data, argmax_t, reward, input_image_data1))

            if len(D) > REPLAY_MEMORY:
                D.popleft()

            if n > OBSERVE:
                minibatch = random.sample(D, BATCH)
                input_image_data_batch = [d[0] for d in minibatch]
                argmax_batch = [d[1] for d in minibatch]
                reward_batch = [d[2] for d in minibatch]
                input_image_data1_batch = [d[3] for d in minibatch]

                gt_batch = []

                out_batch = predict_action.eval(feed_dict = {input_image : input_image_data1_batch})

                for i in range(0, len(minibatch)):
                    gt_batch.append(reward_batch[i] + LEARNING_RATE * np.max(out_batch[i]))

                print("gt_batch:", gt_batch, "argmax:", argmax_batch)
                optimizer.run(feed_dict = {gt : gt_batch, argmax : argmax_batch, input_image : input_image_data_batch})

            input_image_data = input_image_data1
            n = n+1
            print(n, "epsilon:", epsilon, " " ,"action:", maxIndex, " " ,"reward:", reward)

train_neural_network(input_image)

6. 總結

說到這裡，相信你已經能對強化學習有了一個大致的瞭解。接下來的事情，應該是如何把這項技術應用到我們的工作中，讓它發揮出應有的價值。

此文已由作者授權騰訊雲技術社群釋出，轉載請註明文章出處