15年藍橋杯真題——完美正方形
阿新 • • 發佈:2019-01-26
如果一些邊長互不相同的正方形,可以恰好拼出一個更大的正方形,則稱其為完美正方形。
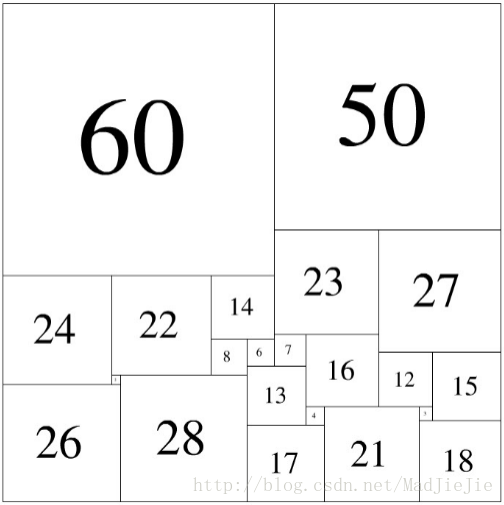
歷史上,人們花了很久才找到了若干完美正方形。比如:如下邊長的22個正方形 2 3 4 6 7 8 12 13 14 15 16 17 18
21 22 23 24 26 27 28 50 60 如【圖1.png】那樣組合,就是一種解法。此時, 緊貼上邊沿的是:60 50
緊貼下邊沿的是:26 28 17 21 18 22階完美正方形一共有8種。下面的組合是另一種: 2 5 9 11 16 17 19 21
22 24 26 30 31 33 35 36 41 46 47 50 52 61 如果告訴你該方案緊貼著上邊沿的是從左到右依次為:47
46 61, 你能計算出緊貼著下邊沿的是哪幾個正方形嗎? 請提交緊貼著下邊沿的正方形的邊長,從左到右,用空格分開。
程式碼如下:
#include <stdio.h> #include <string.h> #define M 154 #define N 19 int num[N]={2,5,9,11,16,17,19,21,22,24,26,30,31,33,35,36,41,50,52}; int map[M][M]={0}; //接收矩陣 void fill(int x,int y,int n,int number); int search(int *numC); int check(int x,int y,int n); int judge(int *numC); int main(void) { int numC[N]={0}; int i=0; memset(map,0,sizeof(map)); memset(numC,0,sizeof(numC)); fill(0,0,47,47); fill(0,47,46,46); fill(0,93,61,61); search(numC); for(i=0;i<M;) { printf("%d ",map[M-1][i]); i+=map[M-1][i]; } } int search(int *numC) { int x=0,y=0; int i=0,j=0,k=0; if(judge(numC)) return 1; for(i=0;i<M;i++) //得到距離(0,0)座標最近的點 { for(j=0;j<M;j++) { if(!map[i][j]) { x = i; y = j; break; } } if(j<M) break; } for(i=0;i<N;i++) //列舉每個小正方形 { if(check(x,y,num[i])) { if(!numC[i]) { numC[i] = 1; fill(x,y,num[i],num[i]); if(search(numC)) return 1; numC[i] = 0; fill(x,y,num[i],0); } } else break; //因為小正方行邊長有序排列,所以當前如果不符合條件,其後也不符合條件,可以直接跳出 } return 0; } void fill(int x,int y,int n,int number) //填充矩陣 { int i=0,j=0; for(i=x;i<x+n;i++) { for(j=y;j<y+n;j++) { map[i][j] = number; } } } int check(int x,int y,int n) //檢查每次防止正方形是否合理 { if(x+n>M||y+n>M) return 0; if(map[x][y+n-1]) return 0; return 1; } int judge(int *numC) //判斷最終條件 { int i=0; for(i=0;i<N;i++) if(!numC[i]) return 0; return 1; }