L型骨牌棋盤覆蓋
題目描述
有一個棋盤，要求用給定的四種骨牌進行覆蓋。四種骨牌定義如下：

 
給定的棋盤中有一個格子不存在，即不需要覆蓋的格子。
輸入
輸入有多個用例，第一個為用例個數n，接下來每個用例佔兩行，其中第一行為棋盤大小（如3，表示棋盤大小為2的3次，即8行8列），第二行為兩個正整數，表示空缺的格子行號和列號。
輸出
每個用例用一行輸出各種骨牌的使用數，用一個空格隔開。
樣例輸入
1
3
1 1
樣例輸出
9 5 5 2

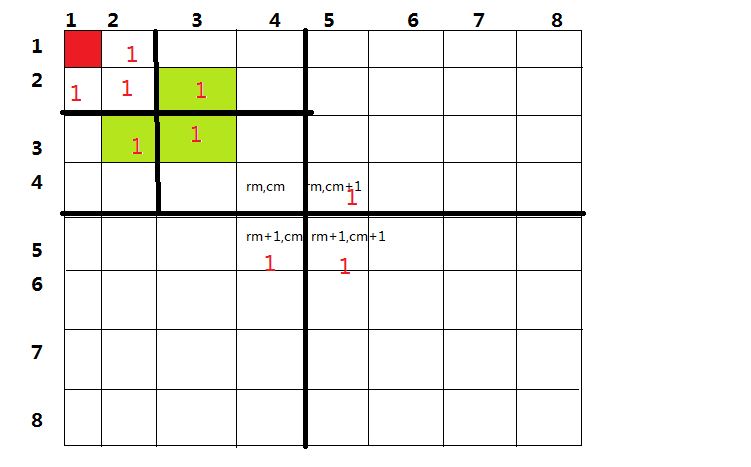
如圖：

1、先判斷缺的瓷磚在整個棋盤的那個位置（左上，右上，左下，右下），缺的瓷磚在1號。

2、在中間放一個對應1號瓷磚。

3、在將再將左上的部分分解，重複直到只有一個瓷磚。

ACcode：

#include <iostream>
#include <cmath>
using namespace std;

int k1,k2,k3,k4;
void work(int rs,int re,int cs,int ce, int u,int w)
{
     if(rs==re)
		 return;
	 int rm = (rs+re)/2;
	 int cm = (cs+ce)/2;

	 if(u<=rm)//處在上部分
	 {
		 if(w<=cm)//處在左部分
		 {
			 k1++;
			  work(rs,rm,cs,cm,u,w);
			  work(rs,rm,cm+1,ce,rm,cm+1); 
			  work(rm+1,re,cs,cm,rm+1,cm); 
			  work(rm+1,re,cm+1,ce,rm+1,cm+1);
              
		 }else //處於右部分
		 {
			     k2++;
				 work(rs,rm,cs,cm,rm,cm);
			     work(rs,rm,cm+1,ce,u,w); 
			     work(rm+1,re,cs,cm,rm+1,cm); 
			     work(rm+1,re,cm+1,ce,rm+1,cm+1);
		 }
	   
	 }else   //下面
	 {
		 if(w<=cm)//處在左部分
		 {
			 k3++;
				 work(rs,rm,cs,cm,rm,cm);
			     work(rs,rm,cm+1,ce,rm,cm+1); 
			     work(rm+1,re,cs,cm,u,w); 
			     work(rm+1,re,cm+1,ce,rm+1,cm+1);
			 
		 }else
		 {
			 k4++;
				 work(rs,rm,cs,cm,rm,cm);
			     work(rs,rm,cm+1,ce,rm,cm+1); 
			     work(rm+1,re,cs,cm,rm+1,cm); 
			     work(rm+1,re,cm+1,ce,u,w);
			 
		 }
	    
	 }

}


int main()
{
	int t,n,u,w;
	cin>>t;
	while(t--)
	{
		k1=k2=k3=k4=0;
		cin>>n>>u>>w;//u,w表示缺的位置
		n = (int)pow(2,n);
	    
		work(1,n,1,n,u,w);
		cout<<k1<<" "<<k2<<" "<<k3<<" "<<k4<<endl;
	}
	return 0;
}