模型組合之梯度提升(Gradient Boosting)
Boosting方法：
Boosting這其實思想相當的簡單，大概是，對一份資料，建立M個模型（比如分類），一般這種模型比較簡單，稱為弱分類器(weak learner)每次分類都將上一次分錯的資料權重提高一點再進行分類，這樣最終得到的分類器在測試資料與訓練資料上都可以得到比較好的成績。
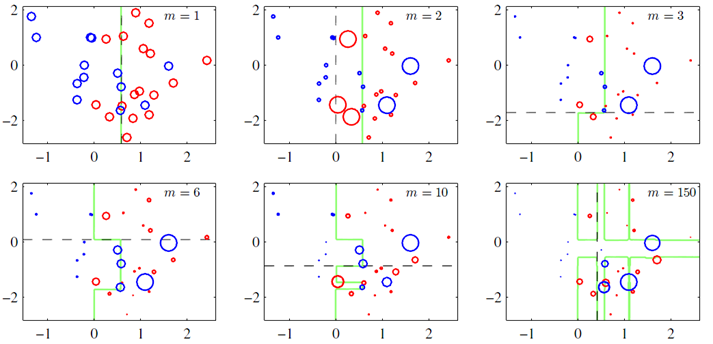
上圖（圖片來自prml p660）就是一個Boosting的過程，綠色的線表示目前取得的模型（模型是由前m次得到的模型合併得到的），虛線表示當前這次模型。每次分類的時候，會更關注分錯的資料，上圖中，紅色和藍色的點就是資料，點越大表示權重越高，看看右下角的圖片，當m=150的時候，獲取的模型已經幾乎能夠將紅色和藍色的點區分開了。
Boosting可以用下面的公式來表示：
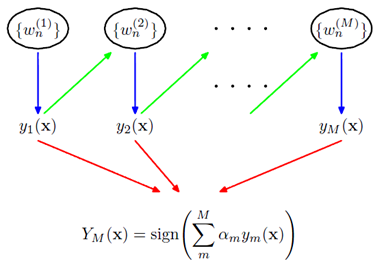
訓練集中一共有n個點，我們可以為裡面的每一個點賦上一個權重Wi(0 <= i < n)，表示這個點的重要程度，通過依次訓練模型的過程，我們對點的權重進行修正，如果分類正確了，權重降低，如果分類錯了，則權重提高，初始的時候，權重都是一樣的。上圖中綠色的線就是表示依次訓練模型，可以想象得到，程式越往後執行，訓練出的模型就越會在意那些容易分錯（權重高）的點。當全部的程式執行完後，會得到M個模型，分別對應上圖的y1(x)…yM(x)，通過加權的方式組合成一個最終的模型YM(x)。
我覺得Boosting更像是一個人學習的過程，開始學一樣東西的時候，會去做一些習題，但是常常連一些簡單的題目都會弄錯，但是越到後面，簡單的題目已經難不倒他了，就會去做更復雜的題目，等到他做了很多的題目後，不管是難題還是簡單的題都可以解決掉了。
Gradient Boosting方法：
其實Boosting更像是一種思想，Gradient Boosting是一種Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型損失函式的梯度下降方向。這句話有一點拗口，損失函式(loss function)描述的是模型的不靠譜程度，損失函式越大，則說明模型越容易出錯（其實這裡有一個方差、偏差均衡的問題，但是這裡就假設損失函式越大，模型越容易出錯）。如果我們的模型能夠讓損失函式持續的下降，則說明我們的模型在不停的改進，而最好的方式就是讓損失函式在其梯度（Gradient)的方向上下降。
下面的內容就是用數學的方式來描述Gradient Boosting，數學上不算太複雜，只要潛下心來看就能看懂：）
可加的引數的梯度表示：
假設我們的模型能夠用下面的函式來表示，P表示引數，可能有多個引數組成，P = {p0,p1,p2….}，F(x;P)表示以P為引數的x的函式，也就是我們的預測函式。我們的模型是由多個模型加起來的，β表示每個模型的權重，α表示模型裡面的引數。為了優化F，我們就可以優化{β,α}也就是P。
我們還是用P來表示模型的引數，可以得到，Φ(P)表示P的likelihood函式，也就是模型F(x;P)的loss函式，Φ(P)=…後面的一塊看起來很複雜，只要理解成是一個損失函式就行了，不要被嚇跑了。
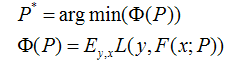既然模型(F(x;P))是可加的，對於引數P，我們也可以得到下面的式子：
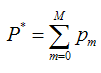這樣優化P的過程，就可以是一個梯度下降的過程了，假設當前已經得到了m-1個模型，想要得到第m個模型的時候，我們首先對前m-1個模型求梯度。得到最快下降的方向，gm就是最快下降的方向。
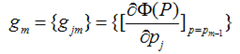這裡有一個很重要的假設，對於求出的前m-1個模型，我們認為是已知的了，不要去改變它，而我們的目標是放在之後的模型建立上。就像做事情的時候，之前做錯的事就沒有後悔藥吃了，只有努力在之後的事情上別犯錯：
我們得到的新的模型就是，它就在P似然函式的梯度方向。ρ是在梯度方向上下降的距離。
我們最終可以通過優化下面的式子來得到最優的ρ：
可加的函式的梯度表示：
上面通過引數P的可加性，得到了引數P的似然函式的梯度下降的方法。我們可以將引數P的可加性推廣到函式空間，我們可以得到下面的函式，此處的fi(x)類似於上面的h(x;α)，因為作者的文獻中這樣使用，我這裡就用作者的表達方法：
同樣，我們可以得到函式F(x)的梯度下降方向g(x)
最終可以得到第m個模型fm(x)的表示式:
通用的Gradient Descent Boosting的框架：
下面我將推導一下Gradient Descent方法的通用形式，之前討論過的：
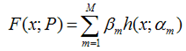對於模型的引數{β,α}，我們可以用下面的式子來進行表示，這個式子的意思是，對於N個樣本點(xi,yi)計算其在模型F(x;α,β)下的損失函式，最優的{α,β}就是能夠使得這個損失函式最小的{α,β}。
表示兩個m維的引數：
寫成梯度下降的方式就是下面的形式，也就是我們將要得到的模型fm(x)的引數{αm,βm}能夠使得fm的方向是之前得到的模型Fm-1(x)的損失函式下降最快的方向：
對於每一個數據點xi都可以得到一個gm(xi)，最終我們可以得到一個完整梯度下降方向
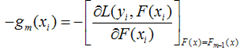為了使得fm(x)能夠在gm(x)的方向上，我們可以優化下面的式子得到，可以使用最小二乘法：
得到了α的基礎上，然後可以得到βm。 
最終合併到模型中：
演算法的流程圖如下