對極幾何（Epipolar Geometry）描述的是兩幅檢視之間的內在射影關係，與外部場景無關，只依賴於攝像機內參數和這兩幅試圖之間的的相對姿態

1. 什麼是對極幾何·粗略概念

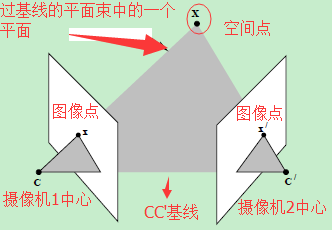
提到對極幾何，一定是對二幅影象而言，對極幾何實際上是“兩幅影象之間的對極幾何”，它是影象平面與以基線為軸的平面束的交的幾何（這裡的基線是指連線攝像機中心的直線），以下圖為例：對極幾何描述的是左右兩幅影象(點x和x’對應的影象)與以CC’為軸的平面束的交的幾何！

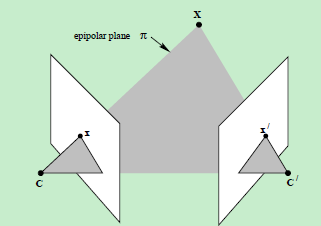
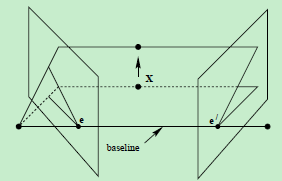
• 直線CC’為基線，以該基線為軸存在一個平面束，該平面束與兩幅影象平面相交，下圖給出了該平面束的直觀形象，可以看到，該平面束中不同平面與兩幅影象相交於不同直線；
  
• 上圖中的灰色平面π，只是過基線的平面束中的一個平面（當然，該平面才是平面束中最重要的、也是我們要研究的平面）；

2. 對極幾何相關的一個重要約束·5點共面約束

仍以上面貼出的影象為例，此處重複貼出，空間點X在兩幅影象中的像分別為x和x’，這兩個投影點之間存在什麼關係呢？觀察下圖

• 點x、x’與攝像機中心C和C’是共面的，並且與空間點X也是空面的，這5個點共面於平面π！這是一個最本質的約束，即5個點決定了一個平面π
• 由該約束，可以推匯出一個重要性質：由影象點x和x’反投影的射線共面，並且，在平面π上，在搜尋點對應中，該性質非常重要

3. 對極幾何的幾個相關概念

• 對極平面束（epipolar pencil）：以基線為軸的平面束；下圖給出了包含兩個平面的對極平面束
  

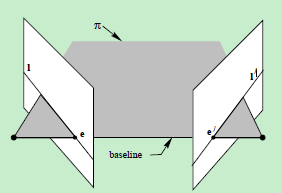
• 對極平面（epipolar plane）：任何包含基線的平面都稱為對極平面，或者說是對極平面束中的平面；例如，下圖中的平面π就是一個對極平面
  

• 對極點（epipole）：攝像機的基線與每幅影象的交點；即上圖中的點e和e’

• 對極線（epipolar line）：對極平面與影象的交線；例如，上圖中的直線l和l’

4. 對應點的約束

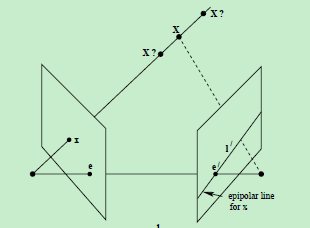
現在假設只知道影象點x，那麼，它的對應點x’如何約束呢？

• 根據前面的討論，點x和x’一定位於平面π上，而平面π可以利用基線CC’和影象點x的反投影射線確定
• 點x’又是右側影象平面上的點，所以，點x’一定位於平面π與右側影象平面的交線l’上
• 前面提到，直線l’為點x的對極線，也就是說，點x的對應點x’一定位於它的對極線上！

Reference
[1]《計算機視覺中的多視幾何》 ·第八章·對極幾何和基本矩陣
[2] 《Multiple View Geometry in Computer Vision Second Edition》·Andrew Zisserman·P239·9 Epipolar Geometry and the Fundamental Matrix