原博文地址：http://blog.csdn.net/xiaowei_cqu/article/details/7693985

多邊形

掃描線演算法是針對計算機中多邊形的顯示。多邊形三條或三條以上的線段首位順次連線所組成的封閉圖形，有凸多邊形（任意兩頂點間的連線均在多邊形內）和凹多邊形（任意兩頂點間的連線有不在多邊形內的部分）。

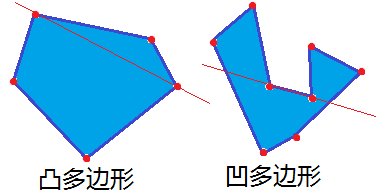
多邊形在計算機中有頂點表示和點陣表示兩種。

頂點表示就是用多邊形的頂點序列來表示多邊形。點陣表示是用位於多邊形內的象素集合來表示多邊形。頂點表示佔記憶體少，幾何意義強，易於進行幾何變換；而點陣表示丟失了許多幾何資訊（如邊界、頂點）。但光柵顯示圖形需要點陣表示形式。

多邊形的掃描轉換

掃描轉換演算法

按掃描線順序，計算掃描線與多邊形的相交區間，再用要求的顏色填充這些區間的象素。步驟如下：

求交：計算掃描線與多邊形各邊的交點； 
排序：把所有交點按x值遞增順序排序； 
配對：第一個與第二個，第三個與第四個等等；每對交點代表掃描線與多邊形的一個相交區間， 
著色：把相交區間內的象素置成多邊形顏色，把相交區間外的象素置成背景色。 

其實很好理解，像下面的圖：

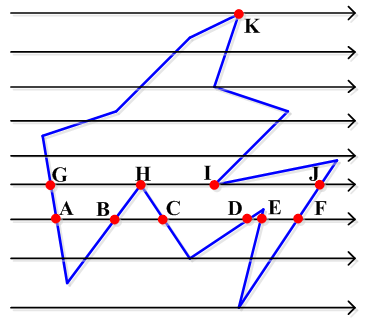
以倒數第三條掃描線為例，有6個交點，排序之後為 A，B，C，D，E，F

然後配對：（A,B）（C,D）（E,F）也就是要填充（A,B）（C,D）（E,F）之間的部分。

這是掃描線與一條邊相交，會出現問題的地方時掃描線與兩條邊相交，也就是與頂點相交。比如ABCD上面那條線，如果把頂點處看做一個交點，如圖，配對的結果是：（G,H）（I,J）於是（H,I）之間的部分就會被填充為背景；如果吧H看做兩個交點，H1,H2。配對結果：(G,H1)（H2,I）。。。把I被看成兩個交點也是不科學的，正確的應該是把H看做0個交點，I看做兩個。

總結說來，就是判斷共享頂點的兩個邊：

如果共享頂點的兩條邊分別落在掃描線的兩邊，交點只算一個；
如果共享頂點的兩條邊在掃描線的同一邊，這時交點作為零個或兩個：另外兩邊都在下面看成0個，都在上面看成2個。
具體實現時，只需檢查頂點的兩條邊的另外兩個端點的y值。按這兩個y值中大於交點y值的個數是0,1,2來決定。

還是上圖GHI那條線，應看做G，I1，I2，J。配對結果：（G,I1）（I2,J）。

上圖所有有交點的地方：

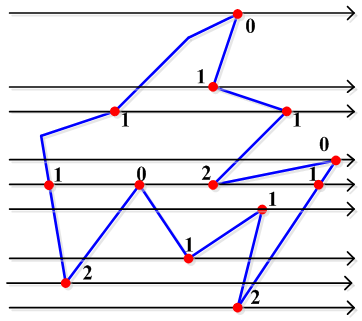
邊相關掃描填充演算法

如果G的交點座標是x1，假設A是下一條掃描線的交點，則交點就是x1+1/m。即：x(i+1)=x(i)+1/m。

這種性質在遇到頂點的時候會有一些改變，可以通過邊的相關性總結規律。簡單描述為掃描線上相鄰畫素的點在多邊形內還是多邊形外，內，外的關係在遇到頂點時會發生改變。還是上面那張圖：

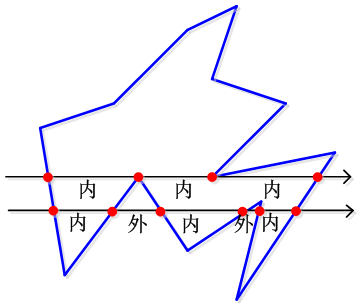
邊相關的填充演算法描述有點複雜，要維護兩張表。回頭再重寫一章吧。

OpenCV中的函式

OpenCV中用 fillPoly() 函式繪製多邊形。在core module的部分有所有的基本繪圖函式：

直線 line()、圓circle()、橢圓ellipse()、矩形rectangle()、填充多邊形fillPoly()

在安裝目錄的  OpenCV2.3.1\samples\cpp\tutorial_code\CxCore\Matrix  的資料夾下有名為  Drawing_1.cpp 的檔案，有所有繪圖的演示。填充多邊形使用如下：

1. void MyPolygon( Mat img )  
2. {  
3.   int lineType = 8;  
4.   /** Create some points */
5.   Point rook_points[1][20];  
6.   rook_points[0][0] = Point( w/4.0, 7*w/8.0 );  
7.   rook_points[0][1] = Point( 3*w/4.0, 7*w/8.0 );  
8.   rook_points[0][2] = Point( 3*w/4.0, 13*w/16.0 );  
9.   rook_points[0][3] = Point( 11*w/16.0, 13*w/16.0 );  
10.   rook_points[0][4] = Point( 19*w/32.0, 3*w/8.0 );  
11.   rook_points[0][5] = Point( 3*w/4.0, 3*w/8.0 );  
12.   rook_points[0][6] = Point( 3*w/4.0, w/8.0 );  
13.   rook_points[0][7] = Point( 26*w/40.0, w/8.0 );  
14.   rook_points[0][8] = Point( 26*w/40.0, w/4.0 );  
15.   rook_points[0][9] = Point( 22*w/40.0, w/4.0 );  
16.   rook_points[0][10] = Point( 22*w/40.0, w/8.0 );  
17.   rook_points[0][11] = Point( 18*w/40.0, w/8.0 );  
18.   rook_points[0][12] = Point( 18*w/40.0, w/4.0 );  
19.   rook_points[0][13] = Point( 14*w/40.0, w/4.0 );  
20.   rook_points[0][14] = Point( 14*w/40.0, w/8.0 );  
21.   rook_points[0][15] = Point( w/4.0, w/8.0 );  
22.   rook_points[0][16] = Point( w/4.0, 3*w/8.0 );  
23.   rook_points[0][17] = Point( 13*w/32.0, 3*w/8.0 );  
24.   rook_points[0][18] = Point( 5*w/16.0, 13*w/16.0 );  
25.   rook_points[0][19] = Point( w/4.0, 13*w/16.0) ;  
26.   const Point* ppt[1] = { rook_points[0] };  
27.   int npt[] = { 20 };  
28.   fillPoly( img,  
29.         ppt,  
30.         npt,  
31.             1,  
32.         Scalar( 255, 255, 255 ),  
33.         lineType );           
34. }  

簡單來說就是定義多邊形的點就可以直接繪製。

效果如下：

還有一個效果很炫的 Drawing_2.cpp ，裡面有Text的演示

尤其喜歡最後的效果：