（一）馬踏棋盤經典演算法描述：

  （1）馬踏棋盤是經典的程式設計問題之一，主要的解決方案有兩種：一種是基於深度優先搜尋的方法，另一種是基於貪婪演算法的方法。第一種基於深度優先搜尋的方法是比較常用的演算法，深度優先搜尋演算法也是資料結構中的經典演算法之一，主要是採用遞迴的思想，一級一級的尋找，遍歷出所有的結果，最後找到合適的解。而基於貪婪的演算法則是制定貪心準則，一旦設定不能修改，他只關心區域性最優解，但不一定能得到最優解。

【問題描述】關於馬踏棋盤的基本過程：國際象棋的棋盤為 8*8 的方格棋盤。現將"馬"放在任意指定的方格中，按照"馬"走棋的規則將"馬"進行移動。要求每個方格只能進入一次，最終使得"馬"走遍棋盤的64個方格。

【演算法分析】

  ① 在四角，馬踏日走只有兩個選擇；

  ② 在其餘部分，馬踏日走有四、六、八不等的選擇。

解決方案：在外層另外加上兩層，確保 8*8 方格中的每一個格子都有8中不同的選擇；

重點：為了確保每個格子能走日字，而且選擇的可能性等同，初始化除了最外兩層格子標記沒有被訪問，最外兩層中每個格子都標記為已被訪問即可達到目標！

解釋：圖片中標記紅色的區域，初始化時就預設為馬已踏日字，集已被訪問，而中間的 8*8 的表格標記為馬未被訪問！

並且每一個表格中馬在訪問時都有8中不同的選擇，這8中不同的選擇都會在其相應的x和y座標上進行追加標記；

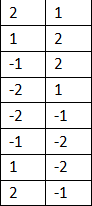
這8中選擇方式為：

【程式碼展示1】：遞迴求解（回溯法求解），列出所有的解，並從中找出從(2,2)位置出發的合適解：

#include <iostream>
#include <stdlib.h>

using namespace std;

int chessboard[12][12] = {0};

int cnt = 0;			//標記馬已走的方格數
int sum = 0;			//標記馬走完全程的具體方案數
int move[8][2]={ {2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};	//初始馬當前位置向其周圍相鄰八個日字的 x,y的偏移量

//輸出馬踏棋盤的解 
void PrintChess();
//馬踏棋盤遞迴過程
void Horse(int x,int y); 

int main(void){
	int i,j;
	for(i=0;i<12;i++){
		for(j=0;j<12;j++){
			if(i==0 || i==1 || i==10 || i==11 || j==0 || j==1 || j==10 || j==11){
				chessboard[i][j]=-1;//在 8 * 8 的外層再加上兩層，確保 8 * 8 方格中的每一個格子都有 8 種不同的日字選擇 
			}
		}
	}
	//從起始位置開始求得所有解
	chessboard[2][2] = ++cnt;
	Horse(2,2);	//遞迴呼叫當前當前位置附近的 8 個日字，看看是否滿足條件
	return 0; 
} 

void Horse(int x,int y){		//馬永遠踏的是 x,y位置，而不是 a,b 
	if(cnt >= 64){		//臨界值，馬走日字全部踏完，成功求出問題解	 
		sum++;
		PrintChess();
		return;
	} 
	for(int i=0;i<8;i++){
		int a = x + move[i][0];		//拿到當前馬位置相鄰的 8 個日字的 x 座標 
		int b = y + move[i][1];		//拿到當前馬位置相鄰的 8 個日字的 y 座標 
		if(chessboard[a][b] == 0){	//判斷當前馬位置相鄰的日字是否已被訪問 
			cnt++;					 
			chessboard[a][b]=cnt;	//標誌已被訪問
			Horse(a,b);			 	//從當前馬的位置繼續往下訪問
			cnt--;					
			chessboard[a][b]=0; 	//回溯回來修改其相鄰的日字的訪問情況 
		}
	}
}

//輸出馬踏棋盤的解 
void PrintChess(){
	cout<<endl<<"馬踏棋盤第 "<<sum<<"組解為:"<<endl;
	int i,j;
	for(i=2;i<10;i++){
		for(j=2;j<10;j++){
			cout<<"  "<<chessboard[i][j]; 
		}
		cout<<endl;
	} 
}
 

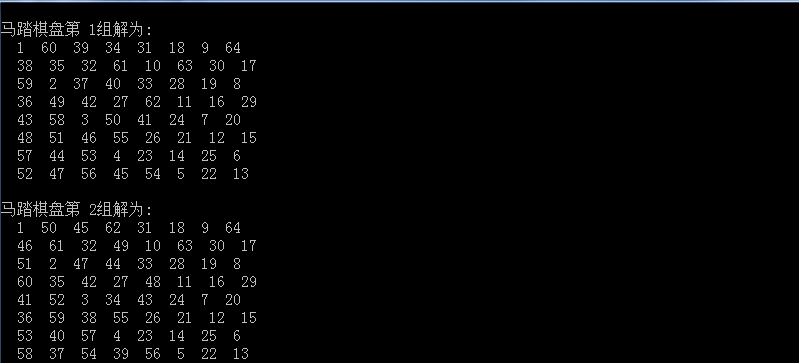
【問題的解】：只列出量兩組解，其餘未列出：

【程式碼展示2】：貪心演算法求解，列出從(2,2)位置出發的合適解，區域性最優：

#include <iostream>
#include <stdlib.h>

using namespace std;

/* 
typedef struct{
	int x;			//記錄當前馬位置的 x 座標		
	int y;			//記錄當前馬位置的 y 座標 
	int i;			//記錄從當前馬的位置前往下一個日字的序號 i (0<i<8) 
}StackHorse; 
*/

int StackHorse[100][3]={0};			//申請一個棧空間(裡面儲存的就是 x,y,i三個具體的變數值)，來標記馬走的具體位置 
int chessboard[12][12] = {0};		//記錄 8 * 8棋盤馬走的具體腳印 
int cnt = 1;			//標記馬已走的方格數
int move[8][2]={ {2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};	//初始馬當前位置向其周圍相鄰八個日字的 x,y的偏移量

//輸出馬踏棋盤的解 
void PrintChess();
//馬踏棋盤遞迴過程
void Horse(int x,int y);

int main(void){
	int i,j;
	for(i=0;i<12;i++){		//初始化馬踏棋盤的具體值(0代表未被訪問，1代表已被訪問，-1代表新加的最外面兩層) 
		for(j=0;j<12;j++){
			if(i==0 || i==1 || i==10 || i==11 || j==0 || j==1 || j==10 || j==11){
				chessboard[i][j]=-1;
			}
		}
	}
	Horse(2,2);		//從 (2,2)的位置開始跑，求得馬踏棋盤的一組解
	PrintChess();
	return 0; 
} 

//非遞迴求一組解的過程
void Horse(int x,int y){
	int top=0,i=0;
	int a,b;				//記錄當前馬位置附近的日字座標
	chessboard[x][y]=1;	//標記當前起始位置已被訪問 

	StackHorse[top][0]=StackHorse[top][1]=2;	//記錄當前馬的位置
	while(cnt < 64){
		for(;i<8;i++){
			a = x + move[i][0];
			b = y + move[i][1];
			if(chessboard[a][b] == 0){		//如果當前馬位置附近的日字沒有被訪問 
				break;						//跳出迴圈 
			}
		}
		if(i<8){					//能夠訪問當前馬位置附近的日字 
			chessboard[a][b]=++cnt;
			StackHorse[top][2]=i;	//記錄訪問當前馬位置附近的日字序號(0<i<8)
			top++;					//top指向新的棧頂
			StackHorse[top][0]=a;	//向新的棧頂放入馬踏入的 x座標	
			StackHorse[top][1]=b;	//向新的棧頂放入馬踏入的 y座標 
			x=a;					//標記新的 x 
			y=b;					//標記新的 y 
			i=0; 					//從棧頂馬位置開始尋找附近的 8 個日字 
		}
		else{			//沒有在當前馬位置附近找到符合條件的日字  
			cnt--;				//回溯 
			chessboard[x][y]=0;
			top--;		//出棧
			x=StackHorse[top][0];		//拿到當前馬位置的 x 座標  
			y=StackHorse[top][1];		//拿到當前馬位置的 y 座標 
			i=StackHorse[top][2];		//拿到當前馬位置前往下一日字的序號 
			i++; 						//繼續搜尋從當前馬位置訪問的日字序號的下一位置繼續訪問 
		} 
	} 
	
} 

//輸出馬踏棋盤的解 
void PrintChess(){
	cout<<"馬踏棋盤一組解為:"<<endl;
	int i,j;
	for(i=2;i<10;i++){
		for(j=2;j<10;j++){
			cout<<"  "<<chessboard[i][j]; 
		}
		cout<<endl;
	} 
}

【問題的解】：列出一組解：