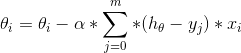本篇部落格主要介紹幾種加速神經網路訓練的方法。

我們知道，在訓練樣本非常多的情況下，如果一次性把所有的樣本送入神經網路，每迭代一次更新網路引數，這樣的效率是很低的。為什麼？因為梯度下降法引數更新的公式一般為：

如果使用批量梯度下降法（一次性使用全部樣本調整引數），那麼上式中求和那項的計算會非常耗時，因為樣本總量m是一個很大的數字。那麼由此就有了第一種加速方法：隨機梯度下降法，簡稱SGD。 它的思想是，將樣本資料挨個送入網路，每次使用一個樣本就更新一次引數，這樣可以極快地收斂到最優值，但會產生較大的波動。還有一種是小批量梯度下降法，它的思想是，將資料拆分成一小批一小批的，分批送入神經網路，每送一批就更新一次網路引數。實驗證明，該方法相比前兩種梯度下降法，集成了兩者的優點，是較好的一種加速方法。

第二類加速方法是加動量項的方法。我們知道，在更新網路引數時，如果前幾次都是朝著一個方向更新，那麼下一次就有很大的可能也是朝著那個方向更新，那麼我們可以利用上一次的方向作為我這次更新的依據。打個比方，我想找到一座山的谷底，當我從山上往山下走，如果第一步是向下，第二步是向下，那麼我第三步就可以走得快一些。從而以這種方式來加速網路訓練。不僅如此，這種方法還可以從一定程度上避免網路陷入到區域性極小值。

當出現以上情況時，網路走到A點，發現梯度已經為零，很可能不再繼續往下走，直接以為A點就是最小值。當我們加上動量項，就可以利用前一時刻的動力，使其衝過A點，繼續往下走。

第三類加速方法是AdamGrad，該方法自動地調整學習率的大小，該方法下的learning rate會根據歷史的梯度值動態地改變學習率的大小。它需要計算更新到該t輪，引數的歷史梯度的平方和。

第四種加速方法是RMSprop，它是一種自適應學習率演算法，它與AdamGrad方法的不同之處在於，它只計算更新到該t輪，引數的歷史梯度的平均值。

第五種加速方法是Adam，它也是一種自適應學習率調整演算法，同時也是最廣泛的一種方法。它利用的是梯度的一階矩估計和二階矩估計。該方法調整的學習率較為平穩，且預估結果較為準確。

當然，還有很多很多種加速神經網路訓練的方法，以上只是較為常見的幾種。

在PyTorch深度學習框架中，實現的優化器覆蓋了Adadelta、Adagrad、Adam、Adamax、RMSprop、Rprop等等。

為了直觀地比較各個優化器的效能，我藉助PyTorch框架用一個神經網路來解決一個二次函式的擬合問題。

import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt

torch.manual_seed(1)  #設定種子，使得結果可再現

LR = 0.01        #學習率learning rate
BATCH_SIZE = 32  #一個batch的大小
EPOCH = 12       #迭代輪數

#製造資料
x = torch.unsqueeze(torch.linspace(-1,1,1000),dim=1) #產生[-1,1]之間的100個值
y = x.pow(2) + 0.1*torch.normal(torch.zeros(x.size())) #y=x^2,再加上0.1倍的正態分佈的擾動

plt.scatter(x.numpy(),y.numpy())
plt.show()    #展示樣本資料

#批訓練
torch_dataset = Data.TensorDataset(data_tensor=x,target_tensor=y)
loader = Data.DataLoader(dataset=torch_dataset,batch_size=BATCH_SIZE,shuffle=True,num_workers=2,)
#shuffle=True表示隨機抽取，num_workers表示執行緒數量

class Net(torch.nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.hidden = torch.nn.Linear(1,20)  #隱層20個神經元
        self.predict = torch.nn.Linear(20,1) #輸出層1個神經元，表示預測的結果

    def forward(self,x):
        x = F.relu(self.hidden(x)) #隱層設定relu啟用函式
        x = self.predict(x)        #輸出層直接線性輸出
        return x

#為每個優化器建立一個Net
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD,net_Momentum,net_RMSprop,net_Adam] #將其放入一個列表中

opt_SGD = torch.optim.SGD(net_SGD.parameters(),lr=LR)
opt_Monentum = torch.optim.SGD(net_Momentum.parameters(),lr=LR,momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(),lr=LR,alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(),lr=LR,betas=(0.9,0.99))
optimizers = [opt_SGD,opt_Monentum,opt_RMSprop,opt_Adam]

#定義誤差函式
loss_func = torch.nn.MSELoss()
losses_his = [[],[],[],[]]

for epoch in range(EPOCH):
    print('Epoch:',epoch)
    for step,(batch_x,batch_y) in enumerate(loader):
        b_x = Variable(batch_x)
        b_y = Variable(batch_y)

        for net,opt,l_his in zip(nets,optimizers,losses_his):
            output = net(b_x)
            loss = loss_func(output,b_y)
            opt.zero_grad()  #為下一次計算梯度清零
            loss.backward()  #誤差反向傳播
            opt.step()       #運用梯度
            l_his.append(loss.data[0])

labels = ['SGD','Momentum','RMSprop','Adam']
for i,l_his in enumerate(losses_his):
    plt.plot(l_his,label=labels[i])
plt.legend(loc='best')  #圖例放在最佳位置
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0,0.2))
plt.show()

原始的訓練資料視覺化：

不同Optimizer優化器效能比較的結果：

結果分析：從上圖中，我們可以看出，SGD明顯波動較大，Adam方法效果最優。當然每種優化器的效能還與訓練資料的分佈有很大的關係。