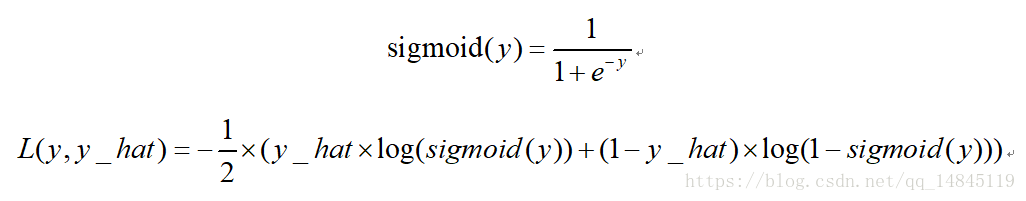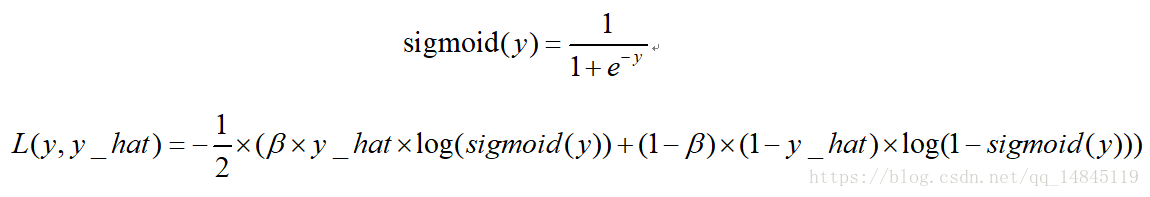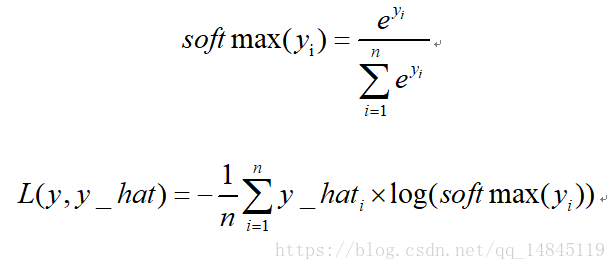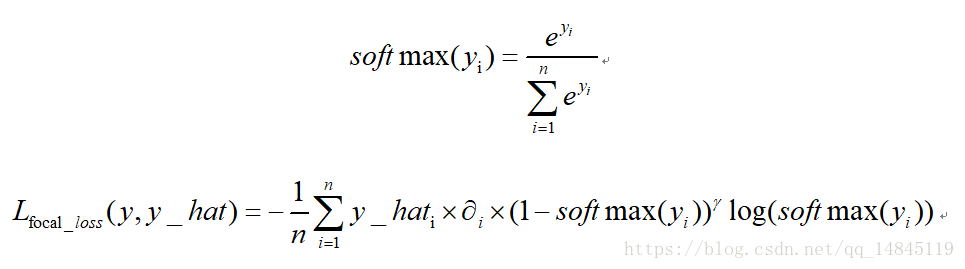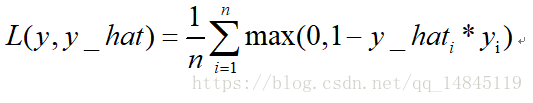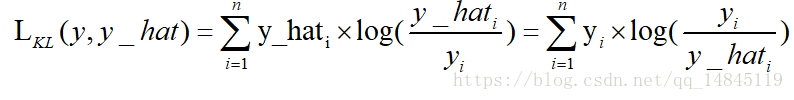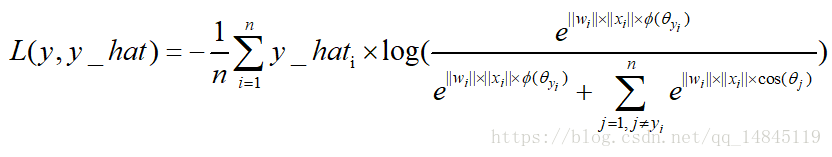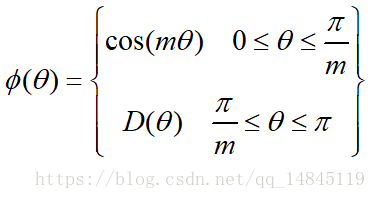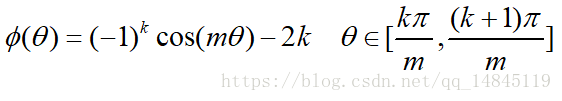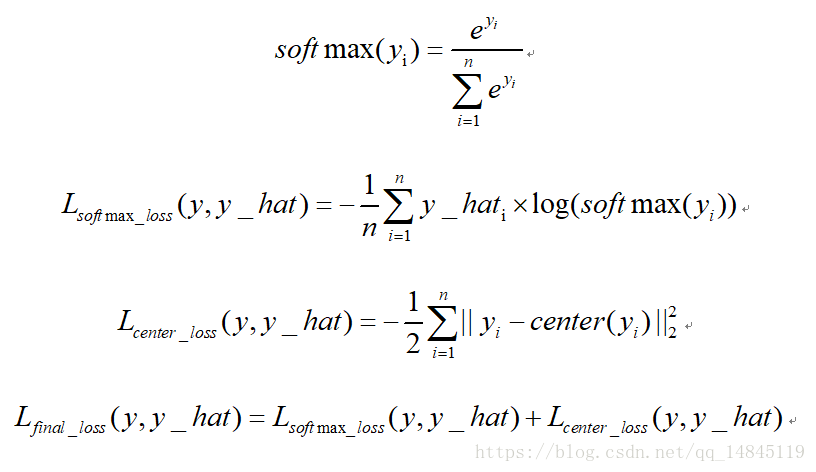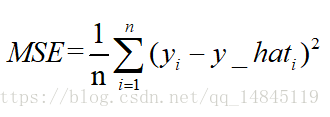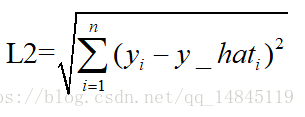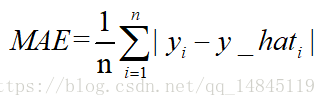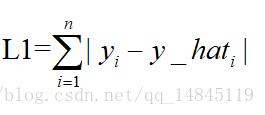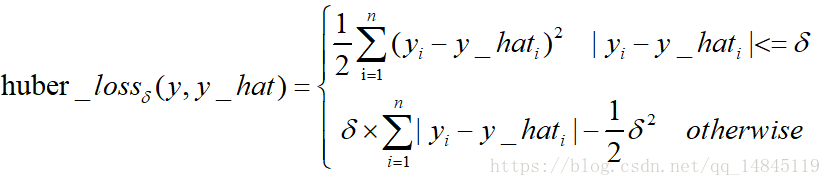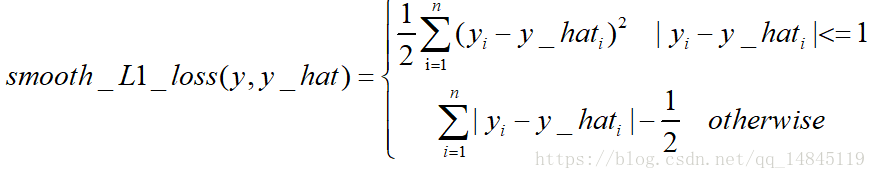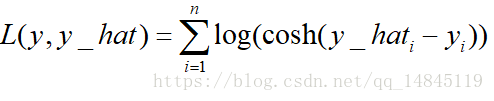損失函式loss大總結
目標函式objectives
目標函式,或稱損失函式,是編譯一個模型必須的兩個引數之一:
model.compile(loss='mean_squared_error', optimizer='sgd')
可以通過傳遞預定義目標函式名字指定目標函式,也可以傳遞一個Theano/TensroFlow的符號函式作為目標函式,該函式對每個資料點應該只返回一個標量值,並以下列兩個引數為引數:
-
y_true:真實的資料標籤,Theano/TensorFlow張量
-
y_pred:預測值,與y_true相同shape的Theano/TensorFlow張量
from keras import losses model.compile(loss=losses.mean_squared_error, optimizer='sgd')
真實的優化目標函式是在各個資料點得到的損失函式值之和的均值
請參考目標實現程式碼獲取更多資訊
可用的目標函式
-
mean_squared_error或mse
-
mean_absolute_error或mae
-
mean_absolute_percentage_error或mape
-
mean_squared_logarithmic_error或msle
-
squared_hinge
-
hinge
-
categorical_hinge
-
binary_crossentropy(亦稱作對數損失,logloss)
-
logcosh
-
categorical_crossentropy:亦稱作多類的對數損失,注意使用該目標函式時,需要將標籤轉化為形如
(nb_samples, nb_classes)的二值序列 -
sparse_categorical_crossentrop:如上,但接受稀疏標籤。注意,使用該函式時仍然需要你的標籤與輸出值的維度相同,你可能需要在標籤資料上增加一個維度:
np.expand_dims(y,-1) -
kullback_leibler_divergence:從預測值概率分佈Q到真值概率分佈P的資訊增益,用以度量兩個分佈的差異.
-
poisson:即
(predictions - targets * log(predictions))的均值 -
cosine_proximity:即預測值與真實標籤的餘弦距離平均值的相反數
注意: 當使用"categorical_crossentropy"作為目標函式時,標籤應該為多類模式,即one-hot編碼的向量,而不是單個數值. 可以使用工具中的to_categorical函式完成該轉換.示例如下:
from keras.utils.np_utils import to_categorical
categorical_labels = to_categorical(int_labels, num_classes=None)分類任務loss:
二分類交叉熵損失sigmoid_cross_entropy:
TensorFlow 介面:
-
tf.losses.sigmoid_cross_entropy( -
multi_class_labels, -
logits, -
weights=1.0, -
label_smoothing=0, -
scope=None, -
loss_collection=tf.GraphKeys.LOSSES, -
reduction=Reduction.SUM_BY_NONZERO_WEIGHTS -
) -
tf.nn.sigmoid_cross_entropy_with_logits( -
_sentinel=None, -
labels=None, -
logits=None, -
name=None -
)
keras 介面:
binary_crossentropy(y_true, y_pred)二分類平衡交叉熵損失balanced_sigmoid_cross_entropy:
該損失也是用於2分類的任務,相比於sigmoid_cross_entrop的優勢在於引入了平衡引數 ,可以進行正負樣本的平衡,得到比sigmoid_cross_entrop更好的效果。
多分類交叉熵損失softmax_cross_entropy:
TensorFlow 介面:
-
tf.losses.softmax_cross_entropy( -
onehot_labels, -
logits, -
weights=1.0, -
label_smoothing=0, -
scope=None, -
loss_collection=tf.GraphKeys.LOSSES, -
reduction=Reduction.SUM_BY_NONZERO_WEIGHTS -
) -
tf.nn.softmax_cross_entropy_with_logits( -
_sentinel=None, -
labels=None, -
logits=None, -
dim=-1, -
name=None -
) -
tf.nn.sparse_softmax_cross_entropy_with_logits( -
_sentinel=None, -
labels=None, -
logits=None, -
name=None -
)
keras 介面:
-
categorical_crossentropy(y_true, y_pred) -
sparse_categorical_crossentropy(y_true, y_pred)
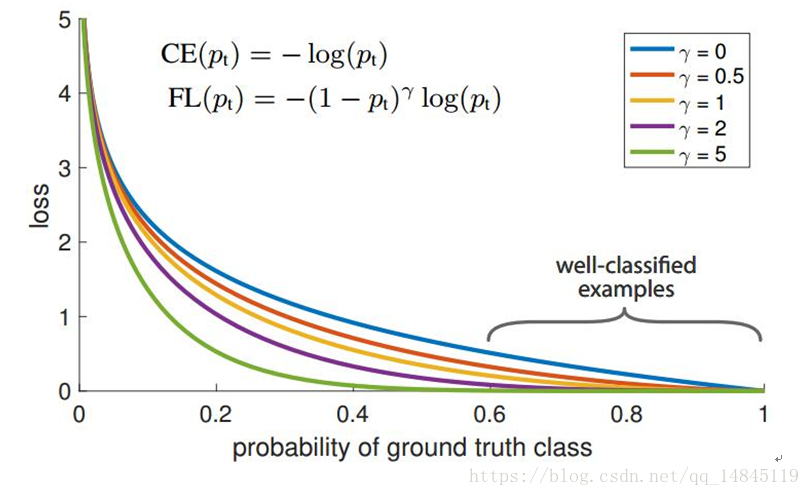
focal loss:
focal loss為凱明大神的大作,主要用於解決多分類任務中樣本不平衡的現象,可以獲得比softmax_cross_entropy更好的分類效果。
論文中α=0.25,γ=2效果最好。
dice loss:
2分類任務時使用的loss,本質就是不斷學習,使得交比並越來越大。
TensorFlow 介面:
-
def dice_coefficient(y_true_cls, y_pred_cls): -
''' -
dice loss -
:param y_true_cls: -
:param y_pred_cls: -
:return: -
''' -
eps = 1e-5 -
intersection = tf.reduce_sum(y_true_cls * y_pred_cls ) -
union = tf.reduce_sum(y_true_cls ) + tf.reduce_sum(y_pred_cls) + eps -
loss = 1. - (2 * intersection / union) -
tf.summary.scalar('classification_dice_loss', loss) -
return loss
合頁損失hinge_loss:
也叫鉸鏈損失,是svm中使用的損失函式。
由於合頁損失優化到滿足小於一定gap距離就會停止優化,而交叉熵損失卻是一直在優化,所以,通常情況下,交叉熵損失效果優於合頁損失。
TensorFlow 介面:
-
tf.losses.hinge_loss( -
labels, -
logits, -
weights=1.0, -
scope=None, -
loss_collection=tf.GraphKeys.LOSSES, -
reduction=Reduction.SUM_BY_NONZERO_WEIGHTS -
)
keras 介面:
hinge(y_true, y_pred)Connectionisttemporal classification(ctc loss):
對於預測的序列和label序列長度不一致的情況下,可以使用ctc計算該2個序列的loss,主要用於文字分類識別和語音識別中。
TensorFlow 介面:
-
tf.nn.ctc_loss( -
labels, -
inputs, -
sequence_length, -
preprocess_collapse_repeated=False, -
ctc_merge_repeated=True, -
ignore_longer_outputs_than_inputs=False, -
time_major=True -
)
keras 介面:
-
tf.keras.backend.ctc_batch_cost( -
y_true, -
y_pred, -
input_length, -
label_length -
)
編輯距離 edit loss:
編輯距離,也叫萊文斯坦Levenshtein 距離,指的是兩個字串之間,由一個轉換成另一個所需的最少編輯操作次數。許可的編輯操作包括將一個字元替換成另一個字元,插入一個字元,刪除一個字元。
該損失函式的優勢在於類似於ctc loss可以計算2個長度不等的序列的損失。
TensorFlow 介面:
-
tf.edit_distance( -
hypothesis, -
truth, -
normalize=True, -
name='edit_distance' -
)
KL散度:
KL散度( Kullback–Leibler divergence),也叫相對熵,是描述兩個概率分佈P和Q差異的一種方法。它是非對稱的,這意味著D(P||Q) ≠ D(Q||P)。特別的,在資訊理論中,D(P||Q)表示當用概率分佈Q來擬合真實分佈P時,產生的資訊損耗,其中P表示真實分佈,Q表示P的擬合分佈。
TensorFlow 介面:
-
tf.distributions.kl_divergence( -
distribution_a, -
distribution_b, -
allow_nan_stats=True, -
name=None -
) -
tf.contrib.distributions.kl( -
dist_a, -
dist_b, -
allow_nan =False, -
name=None -
)
最大間隔損失large margin softmax loss:
用於拉大類間距離的損失函式,可以訓練得到比傳統softmax loss更好的分類效果。
最大間隔損失主要引入了夾角cos值進行距離的度量。假設bias為0的情況下,就可以得出如上的公式。
其中fai(seita)需要滿足下面的條件。
為了進行距離的度量,在cos夾角中引入了引數m。該m為一個正整數,可以起到控制類間間隔的作用。M越大,類間間隔越大。當m=1時,等價於傳統交叉熵損失。基本原理如下面公式
論文中提供的滿足該條件的公式如下
中心損失center loss:
中心損失主要主要用於減少類內距離,雖然只是減少了累內距離,效果上卻可以表現出累內距離小了,類間距離就可以增大的效果。該損失不可以直接使用,需要配合傳統的softmax loss一起使用。可以起到比單純softmax loss更好的分類效果。
迴歸任務loss:
均方誤差mean squareerror(MSE)和L2範數:
MSE表示了預測值與目標值之間差值的平方和然後求平均
L2損失表示了預測值與目標值之間差值的平方和然後開更方,L2表示的是歐幾里得距離。
MSE和L2的曲線走勢都一樣。區別在於一個是求的平均np.mean(),一個是求的更方np.sqrt()
TensorFlow 介面:
-
tf.losses.mean_squared_error( -
labels, -
predictions, -
weights=1.0, -
scope=None, -
loss_collection=tf.GraphKeys.LOSSES, -
reduction=Reduction.SUM_BY_NONZERO_WEIGHTS -
) -
tf.metrics.mean_squared_error( -
labels, -
predictions, -
weights=None, -
metrics_collections=None, -
updates_collections=None, -
name=None -
)
keras 介面:
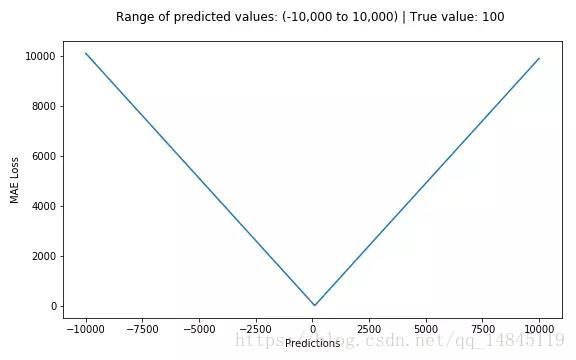
mean_squared_error(y_true, y_pred)平均絕對誤差meanabsolute error(MAE )和L1範數:
MAE表示了預測值與目標值之間差值的絕對值然後求平均
L1表示了預測值與目標值之間差值的絕對值,L1也叫做曼哈頓距離
MAE和L1的區別在於一個求了均值np.mean(),一個沒有求np.sum()。2者的曲線走勢也是完全一致的。
TensorFlow 介面:
-
tf.metrics.mean_absolute_error( -
labels, -
predictions, -
weights=None, -
metrics_collections=None, -
updates_collections=None, -
name=None -
)
keras 介面:
mean_absolute_error(y_true, y_pred)MSE,MAE對比:
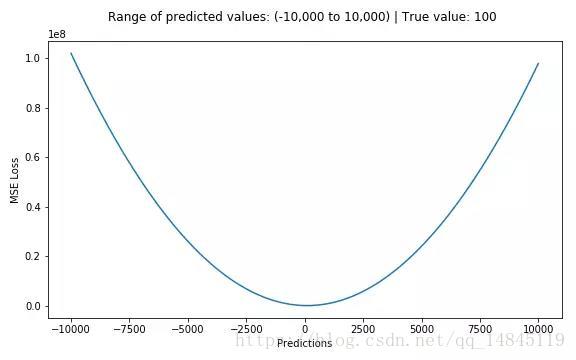
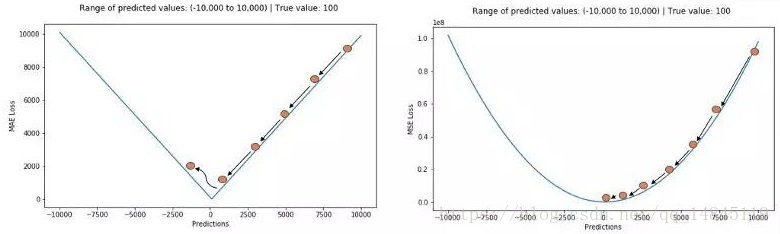
MAE損失對於局外點更魯棒,但它的導數不連續使得尋找最優解的過程低效;MSE損失對於局外點敏感,但在優化過程中更為穩定和準確。
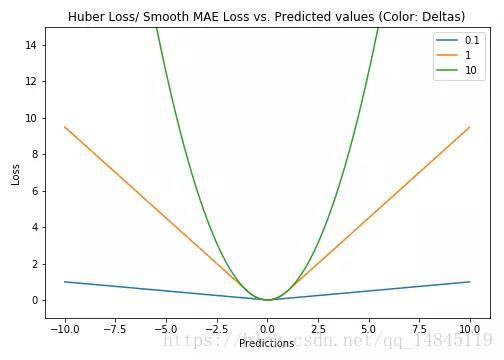
Huber Loss和smooth L1:
Huber loss具備了MAE和MSE各自的優點,當δ趨向於0時它就退化成了MAE,而當δ趨向於無窮時則退化為了MSE。
Smooth L1 loss也具備了L1 loss和L2 loss各自的優點,本質就是L1和L2的組合。
Huber loss和Smooth L1 loss具有相同的曲線走勢,當Huber loss中的δ等於1時,Huber loss等價於Smooth L1 loss。
對於Huber損失來說,δ的選擇十分重要,它決定了模型處理局外點的行為。當殘差大於δ時使用L1損失,很小時則使用更為合適的L2損失來進行優化。
Huber損失函式克服了MAE和MSE的缺點,不僅可以保持損失函式具有連續的導數,同時可以利用MSE梯度隨誤差減小的特性來得到更精確的最小值,也對局外點具有更好的魯棒性。
但Huber損失函式的良好表現得益於精心訓練的超引數δ。
TensorFlow介面:
-
tf.losses.huber_loss( -
labels, -
predictions, -
weights=1.0, -
delta=1.0, -
scope=None, -
loss_collection=tf.GraphKeys.LOSSES, -
reduction=Reduction.SUM_BY_NONZERO_WEIGHTS -
)
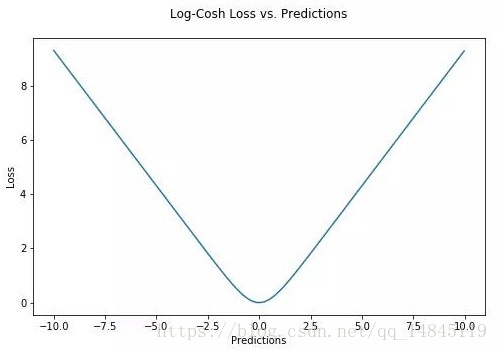
對數雙曲餘弦logcosh:
其優點在於對於很小的誤差來說log(cosh(x))與(x**2)/2很相近,而對於很大的誤差則與abs(x)-log2很相近。這意味著logcosh損失函式可以在擁有MSE優點的同時也不會受到局外點的太多影響。它擁有Huber的所有優點,並且在每一個點都是二次可導的。
keras 介面:
logcosh(y_true, y_pred)