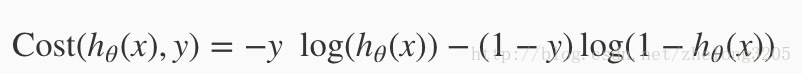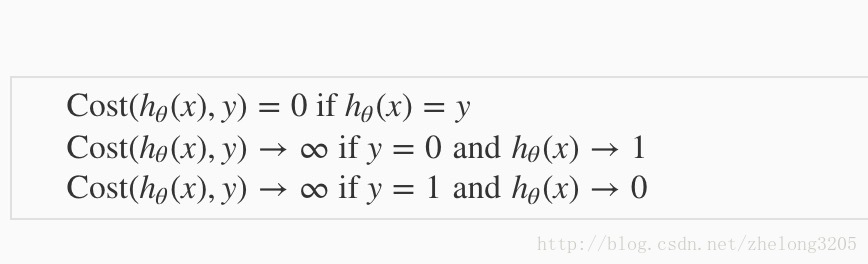logistic regression model

這個模型是用來解決分類問題的一種常用的模型，當然在解決這個種模型的時候仍然需要用到梯度下降法。
在這個模型中 我們設定一個個 cost function (x,y);

它等於下面的一個等式

關於這個公式的來源，並不是沒有他內在的數學原理，他的數學原理需要用到概率論中的極大似然估計法，以及高等數學中的微積分，如果感興趣的話可以看一下這個部落格 解釋的十分詳細 ：

我們注意到這個函式的一個特徵

cost 是預測出來的值，我們發現這個函式可以充分反映出 theta 與 y 的偏差。

其中的 h 函式為

因為 y 的取值只有 0 和 1 所以說這個函式還是可以充分反映出代價函式的變化的。至於為什麼選擇這樣的一個函式原因有下面兩點
1. 這個函式可以更快、更方便的找到 theta 的值
2. 這個函式有一個隱藏的優點就是，這個函式自身是一個凸函式，這樣就保證了我們在使用梯度下降的時候可以收斂到一個區域性最優解，這是非常必要的

這個時候我們得到的代價函式 J (theta) 便也得到了這個函式的表示式

我們現在的目的便是最小化這個函式 J 。
最小化函式我們學過兩種辦法，一種叫做正規方程法，另外一種叫做梯度下降法，由於正規方程法只適用於線性迴歸 （因為線性模型在求導的時候具有特殊的形式，解導數等於零就可以解出這個特殊方程，但是要注意這個方程可能沒有解），所以我們在最小化這個 函式的時候要用到梯度下降法。

梯度下降法的所有的條件不變類似於什麼 標準化還是需要的，特點也存在，那個便是這個j 的偏導數。

這基本上就是整個模型的演算法流程，得到theta 的值以後就可以對新出現的值進行預測了

# 將包匯入
 

import tensorflow as tf 
import numpy as np 
from  tensorflow.examples.tutorials.mnist  import  input_data
import matplotlib as plt 


# 讀取 moist 資料集
mnist = input_data.read_data_sets('data', one_hot = True)

# 設定引數
num_classes = 10 # 要分成 10 類 
input_size = 784 # 因為 moist的資料集每張圖片有 28 ＊ 28 * 1個畫素點
training_iterations = 10000
 
 # 訓練迭代次數
batch_size = 64 # 分批訓練 一次取64個 batch 進行訓練 (batch 應該儘量取大一點)


#使用 placeholder 進行佔位 None 表示第一維度大小任意
X = tf.placeholder (tf.float32, shape = [None, input_size])
Y = tf.placeholder (tf.float32, shape = [None, num_classes])

# 使用 高維線性邊界，假設邊界引數
W = tf.Variable (tf.random_normal ([input_size,num_classes], stddev = 0.1)) 
b = tf.Variable (tf.constant (0.1), [num_classes])

# 計算預測值
y_pred = tf.nn.softmax (tf.matmul (X,W) + b)

# 搭建計算圖 
loss = tf.reduce_mean (tf.square (Y - y_pred))
# loss 使用均方誤差
opt = tf.train.GradientDescentOptimizer (0.05).minimize (loss)
# 使用梯度下降的方法最小化誤差 0.05 是學習率
init = tf.global_variables_initializer ()
correct_prediction = tf.equal (tf.argmax (Y,1), tf.argmax (y_pred,1)) # 計算正確的個數 argmax 函式第一維表示 資料集 1 表示按照行 0 表示按照列 如果沒有的話 表示整體求最大值 返回最大值所在的下標向量，然後 equal 對兩個向量進行比較 相同得到1 不同得到0 
accuracy = tf.reduce_mean (tf.cast (correct_prediction, 'float')) 
# 對上面得到的正確率取平均

# 進行迭代運算
sess = tf.Session ()
sess.run (init)
for i in range (training_iterations) :
    batch = mnist.train.next_batch (batch_size) # 每次取出 64 個 資料進行訓練
    batch_input = batch[0] # 取出資料的第一維就是 輸入的影象
    batch_labels = batch[1] # 取出第二維 就是 它的 label 值 
    training_loss = sess.run ([opt, loss], feed_dict = {X: batch_input, Y: batch_labels})
    # 計算當前的損失值
    if i % 1000 == 0 :
        train_accuracy = accuracy.eval (session = sess, feed_dict = {X: batch_input,Y: batch_labels})
        print ("step : %d, training accuracy = %g " % (i, train_accuracy)) # 列印正確率