卷積與圓周卷積
matlab中fft函式是對序列做DFT,第二個引數是取樣點的數量,當預設時,預設為輸入訊號序列的長度;當大於訊號序列的長度時候,對輸入序列後面補零計算,頻域訊號的解析度因此而變細,但是這時候的解析度是偽解析度。
設定訊號序列s1,length(s1) = 9
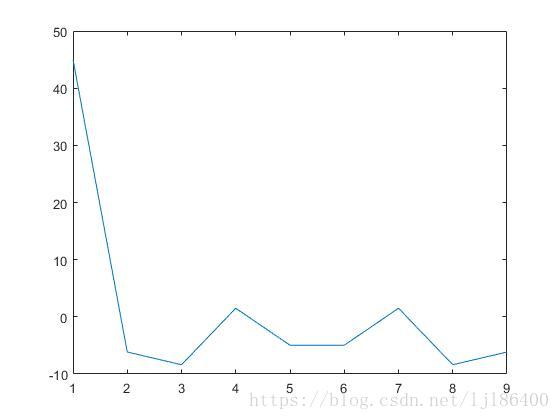
s1 = [1,7,8,9,5,4,6,3,2]呼叫fft函式,對s1進行傅立葉變換
plot(real(fft(s1)))結果如下
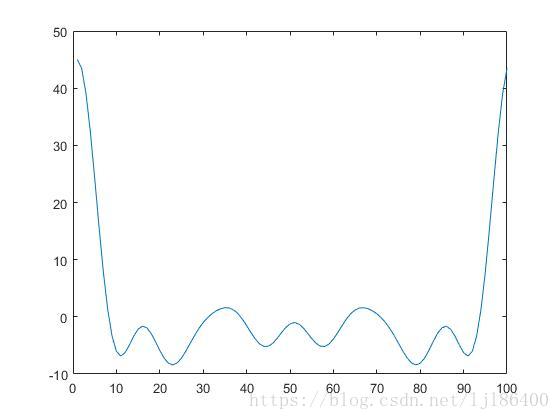
將第二個引數設定成100
figure
plot(real(fft(s1,100)))結果為
通過對比可以看出,補零進行傅立葉變換的結果是頻域圖形的解析度變高了,但仍應注意此時候的解析度是偽解析度。
因為 DTFT(卷積(s1,s2)) = DTFT(s1)*DTFT(s2),因此想通過Matlab中的fft函式獲得線卷積的,可以通過對 IDTFT(DTFT(卷積(s1,s2)) ))取樣獲得,取樣點數 N= length(s1) + length(s2),但是IDTFT(DTFT(卷積(s1,s2)) ))是解析計算式,不容易通過計算機計算獲得結果,只能是對DFT(s1,N)*DFT(s2,N)的結果做傅立葉逆變換,在matlab中實現方法。
ifft(fft(s1,N).*fft(s2,N))同時以上的fft(s1,N).*fft(s2,N)也符合迴圈卷積的頻域表現形式,也就是說conv(s1,s2) = 迴圈卷積(S1,S2),迴圈卷積的輸入訊號S1、S2分別為(這兩者的相等也可以直接通過線性卷積和卷積的運演算法則進行驗證
S1 = (s1,zeros(1,N+1-length(s2)))
S2= (s2,zeros(1,N+1-length(s1)))
因此對於conv(s1,s2) 這種計算量比較大的計算需求,就先補零轉換成迴圈卷積 (S1,S2),再轉換到頻域相乘以縮減計算量,相乘後轉換回到時域就是迴圈卷積 (S1,S2)的結果,也就是conv(s1,s2)的結果了,當s1、s2的序列越長,計算資源的節省效果就越明顯。
PS:通過以上分析也可以看出,通過ifft(fft(s1).*fft(s2))算出來的不是s1、s2的卷積結果,而是他們的迴圈卷積結果,要計算卷積結果可以通過conv(s1,s2)進行計算。