HDU 2046 骨牌鋪方格【遞推】
阿新 • • 發佈:2019-02-07
骨牌鋪方格
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 28606 Accepted Submission(s): 13877
例如n=3時,為2× 3方格,骨牌的鋪放方案有三種,如下圖:
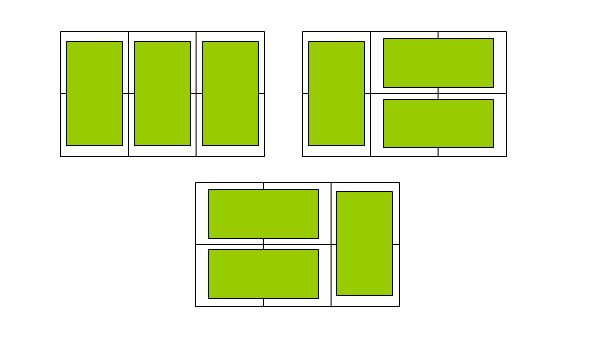 Input
輸入資料由多行組成,每行包含一個整數n,表示該測試例項的長方形方格的規格是2×n (0<n<=50)。
Input
輸入資料由多行組成,每行包含一個整數n,表示該測試例項的長方形方格的規格是2×n (0<n<=50)。Output 對於每個測試例項,請輸出鋪放方案的總數,每個例項的輸出佔一行。
Sample Input 1 3 2 Sample Output 1 3 2 Author lcy
解題思路:設f(n)為當前鋪放的總數。n表示長方形方格的規格是2 X n。
當n=1時,f(n)=1。(一塊骨牌只能豎放)
當n=2時,f(n)=2。(兩塊骨牌都橫放或者都豎放)
當n>=3時,①第n張牌可以豎著放在第n-1張牌的末尾,此時有f(n-1)種情況。
②可以在第n-2張牌的末尾橫著放兩張牌(如果豎著放則與上面的情況重複),此時有f(n-2)種情況。
由此可得遞推公式:f(n)=f(n-1)+f(n-2)
也是簡單的斐波那契數列。
#include<stdio.h> __int64 a[55]={0,1,2,3}; void f() { int i; for(i=4;i<55;i++) a[i]=a[i-1]+a[i-2]; } int main() { f(); int n; while(~scanf("%d",&n)) { printf("%I64d\n",a[n]); } return 0; }
