為了感謝大神，我是跪在電腦前fork的。

問題描述與動機：

• 大家都知道的，其實我們就是在給定的影象畫素向量x和對應的函式f(x)，然後我們希望能夠計算f在x上的梯度(∇f(x))

• 我們之所以想解決這個問題，是因為在神經網路中，f對應損失函式L，而輸入x則對應訓練樣本資料和神經網路的權重W。舉一個特例，損失函式可以是SVM loss function，而輸入則對應樣本資料(xi,yi),i=1…N和權重W以及偏移項b。需要注意的一點是，在我們的場景下，通常我們認為訓練資料是給定的，而權重是我們可以控制的變數。因此我們為了更新權重的等引數，使得損失函式值最小，我們通常是計算f對引數W

  ,b的梯度。不過我們計算其在xi上的梯度有時候也是有用的，比如如果我們想做視覺化以及瞭解神經網路在『做什麼』的時候。

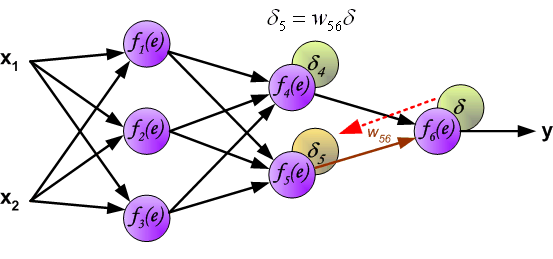
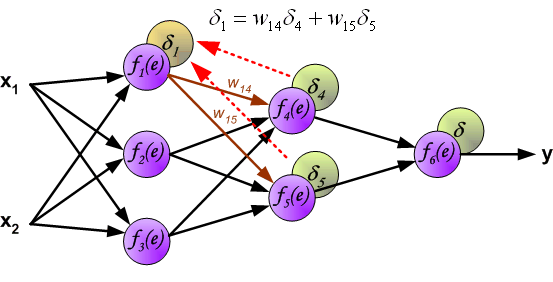
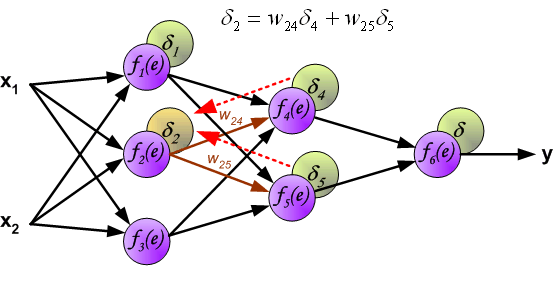
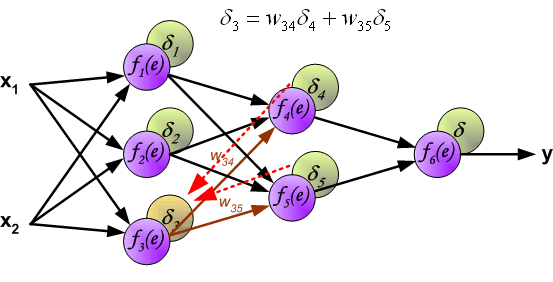
直觀地理解，反向傳播可以看做圖解求導的鏈式法則。 

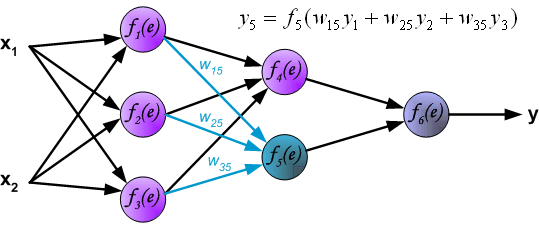
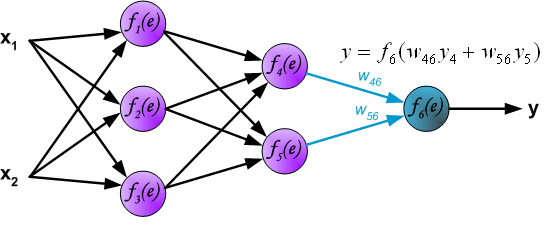
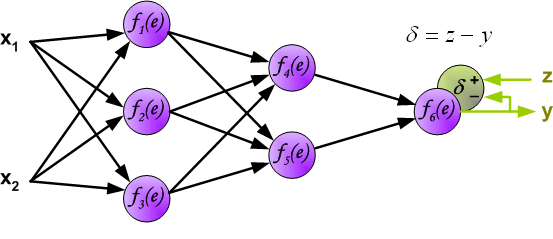
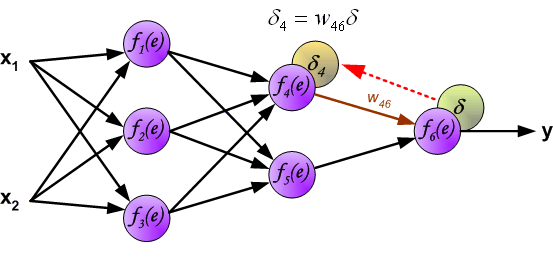
最後我們用一組圖來說明實際優化過程中的正向傳播與反向殘差傳播： 

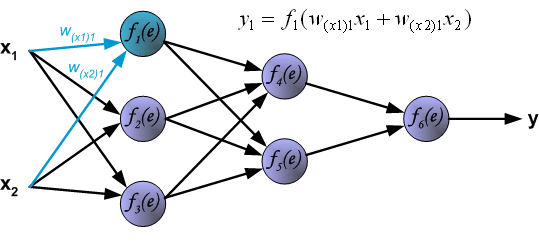
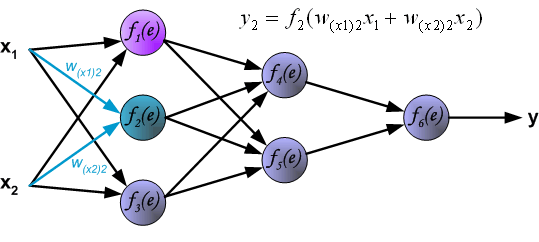
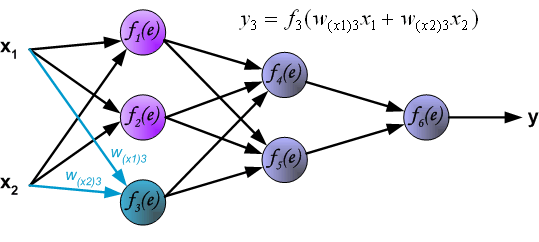
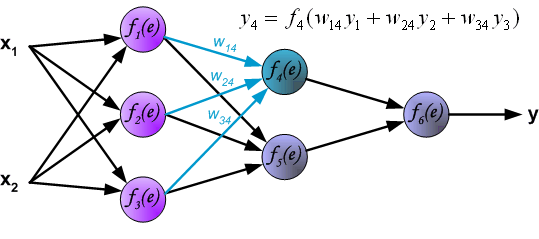
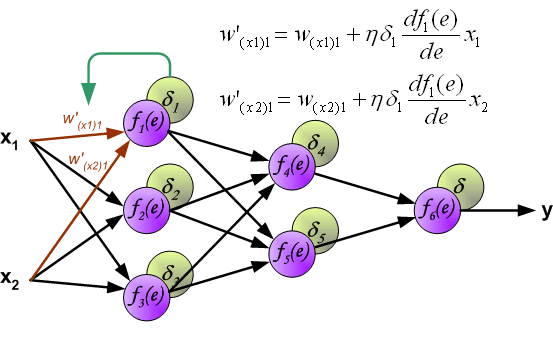
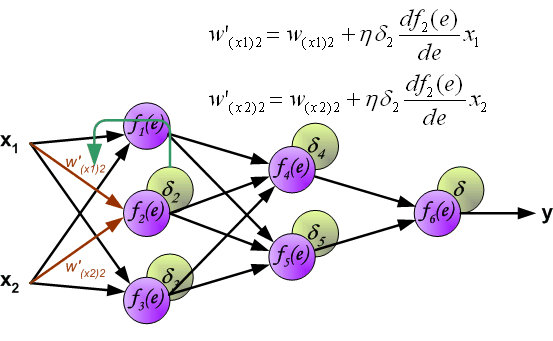
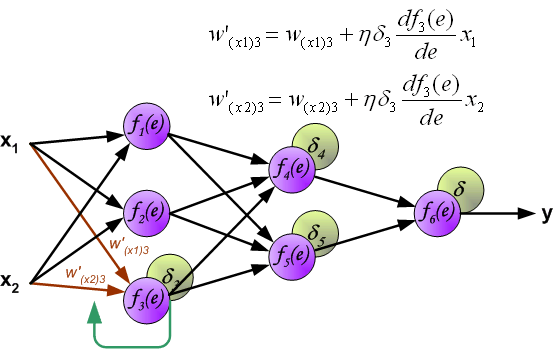
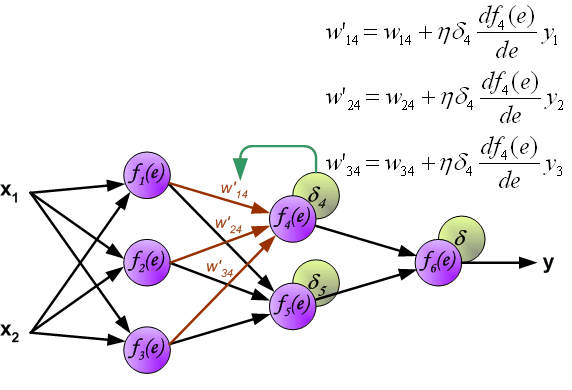
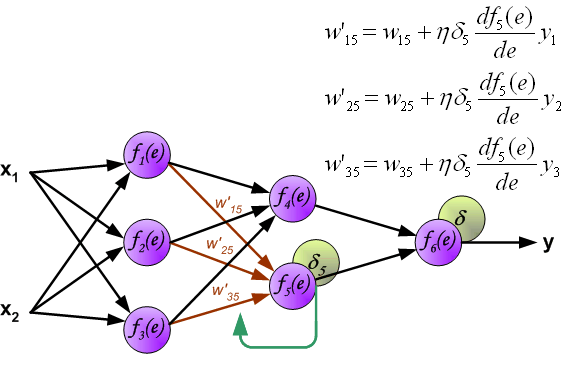
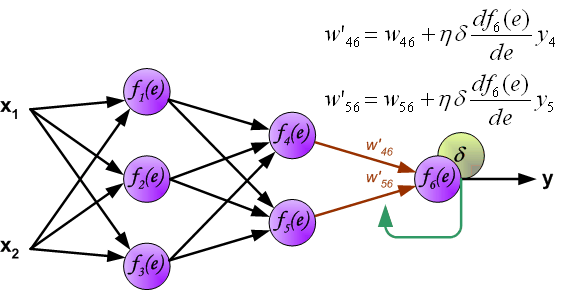
如果幫到你了，請讚賞支援：