Henriques, João F., et al. “High-speed tracking with kernelized
correlation filters.” Pattern Analysis and Machine Intelligence, IEEE
Transactions on 37.3 (2015): 583-596.

本文的跟蹤方法效果甚好，速度奇高，思想和實現均十分簡潔。其中利用迴圈矩陣進行快速計算的方法尤其值得學習。另外，作者在主頁上十分慷慨地給出了各種語言的實現程式碼。
本文詳細推導論文中的一系列步驟，包括論文中未能闡明的部分。請務必先參看這篇簡介迴圈矩陣性質的

思想

一般化的跟蹤問題可以分解成如下幾步：
1. 在It幀中，在當前位置pt附近取樣，訓練一個迴歸器。這個迴歸器能計算一個小視窗取樣的響應。
2. 在It+1幀中，在前一幀位置pt附近取樣，用前述迴歸器判斷每個取樣的響應。
3. 響應最強的取樣作為本幀位置pt+1。

迴圈矩陣表示影象塊

在影象中，迴圈位移操作可以用來近似取樣視窗的位移。

訓練時，圍繞著當前位置進行的一系列位移取樣可以用二維分塊迴圈矩陣X表示，第ij塊表示原始影象下移i行右移j列的結果。類似地，測試時，前一幀結果附近的一系列位移取樣也可以用X表示。

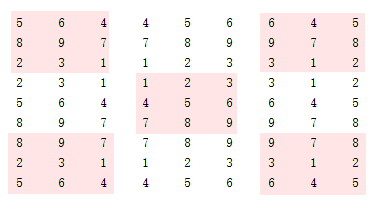
這樣的X可以利用傅立葉變換快速完成許多線性運算。

線性迴歸訓練提速

此部分頻繁用到了迴圈矩陣的各類性質，請參看這篇部落格。
線性迴歸的最小二乘方法解為：

根據迴圈矩陣乘法性質，XHX的特徵值為x^⊙x^∗。I本身就是一個迴圈矩陣，其生成向量為[1,0,0...0]，這個生成向量的傅立葉變換為全1向量，記為δ。

根據迴圈矩陣求逆性質，可以把矩陣求逆轉換為特徵值求逆。

利用F的酉矩陣性質消元：

分號表示用1進行對位相除。
反用對角化性質：Fdiag(y)FH=C(F−1(y))，上式的前三項還是一個迴圈矩陣。

利用迴圈矩陣卷積性質F(C(x)⋅y)=x^∗⊙y^：