定義概覽

　　Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法，用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件，直到擴充套件到終點為止。注意該演算法要求圖中不存在負權邊。

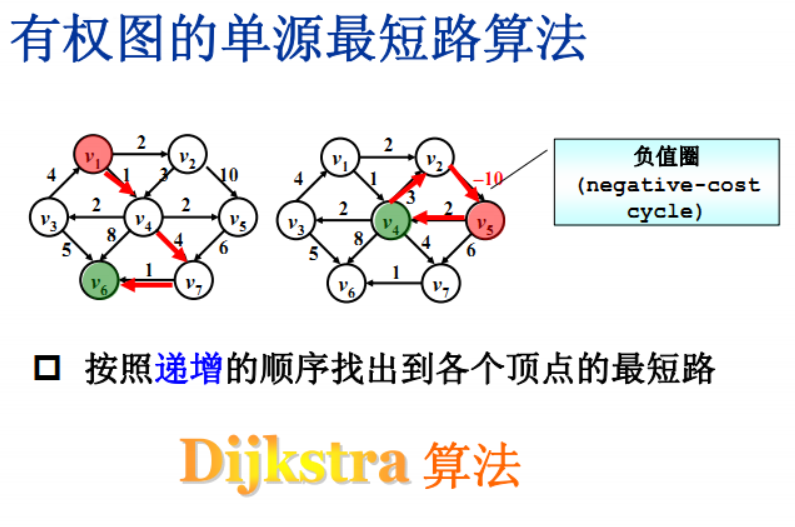
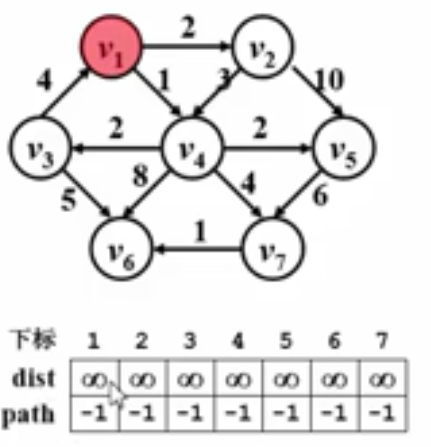
我的理解

　　從開始頂點出發，先將開始頂點吃入（即標記已訪問）

　　　　1。找其最短的邊所連的頂點

　　　　2。將其吃入（即標記已訪問）

　　　　3。遍歷與其相連的其他頂點

　　　　4。若從V 到W距離小於之前到W的距離，則修改（更新）

　　　　5。可以用個堆疊來儲存路徑

　　　　6。迴圈1~4 更新距離， 直至所有的頂點都已經吃入

（1）dist　表示從這個點（陣列序號）到原點的最短距離，每次也更新這裡

（2）path　用來表示路徑

（3）注意：第一次是要把入口頂點所在的邊吃入先——–這步初始化別忘了

/* 鄰接矩陣儲存 - 有權圖的單源最短路演算法 */

Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收錄頂點中dist最小者 */
    Vertex MinV, V;
    int MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) {
        if
 
 ( collected[V]==false && dist[V]<MinDist) {
            /* 若V未被收錄，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距離 */
            MinV = V; /* 更新對應頂點 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回對應的頂點下標 */
    else return ERROR;  /* 若這樣的頂點不存在，返回錯誤標記 */
 

}

bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
    int collected[MaxVertexNum];
    Vertex V, W;

    /* 初始化：此處預設鄰接矩陣中不存在的邊用INFINITY表示 */
    for ( V=0; V<Graph->Nv; V++ ) {
        dist[V] = Graph->G[S][V];
        if ( dist[V]<INFINITY )
            path[V] = S;
        else
            path[V] = -1;
        collected[V] = false;
    }
    /* 先將起點收入集合 */
    dist[S] = 0;
    collected[S] = true;

    while (1) {
        /* V = 未被收錄頂點中dist最小者 */
        V = FindMinDist( Graph, dist, collected );
        if ( V==ERROR ) /* 若這樣的V不存在 */
            break;      /* 演算法結束 */
        collected[V] = true;  /* 收錄V */
        for( W=0; W<Graph->Nv; W++ ) /* 對圖中的每個頂點W */
            /* 若W是V的鄰接點並且未被收錄 */
            if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
                if ( Graph->G[V][W]<0 ) /* 若有負邊 */
                    return false; /* 不能正確解決，返回錯誤標記 */
                /* 若收錄V使得dist[W]變小 */
                if ( dist[V]+Graph->G[V][W] < dist[W] ) {
                    dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
                    path[W] = V; /* 更新S到W的路徑 */
                }
            }
    } /* while結束*/
    return true; /* 演算法執行完畢，返回正確標記 */
}

坑點：

　　高速公路是雙方向的。一開始我以為是單方向的，然後就只過了一個用例。第一次練這題，所以有點囉嗦，請見諒！

//07-圖6 旅遊規劃   (25分)

#include<cstdio>

using namespace std;
#define MAXN 505
#define INFINITY 505

struct City{
    int len;
    int fees;
};

int N;  //城市的個數 編號 0 ~ (N - 1)
int M;  //高速公路的條數
int S;  //出發地的城市編號
int D;  //目的城市編號
City city[MAXN][MAXN];  //圖
int flag[MAXN]; //標記
City dist[MAXN];   //dist表示 這個點到原點的最短路徑
int Length;    //路徑長度
int Fees;  //收費額

void init(){
    for(int i = 0; i < N; ++i){
        for(int j = 0; j < N; ++j){
            city[i][j].len = INFINITY;
            city[i][j].fees = INFINITY;
        }
    }
    for(int i = 0; i < N; ++i){
        dist[i].len = INFINITY;
        dist[i].fees = INFINITY;
    }
}

void setDistValue(int s, int i, int j){
    dist[S].len = i;
    dist[S].fees = j;
}

int findMinDist(){
    City minDist;
    minDist.fees = INFINITY;
    minDist.len = INFINITY;

    int V;  //用於返回的頂點

    for(int i = 0; i < N; ++i){
        if(flag[i] == 0){
            if(dist[i].len < minDist.len){
                minDist.len = dist[i].len;
                minDist.fees = dist[i].fees;
                V = i;
            }else if(dist[i].len == minDist.len){
                if(dist[i].fees < minDist.fees)
                    minDist.fees = dist[i].fees;
            }
        }
    }
    if(minDist.len < INFINITY)
        return V;       //返回對應的頂點下標
    else    return -1;  //這樣的頂點不存在，返回錯誤標記
}

void dijkstra(){
    setDistValue(S, 0, 0);  //將起點吃入集合
    flag[S] = 1;            //標記
    for(int i = 0 ;i < N; ++i){
        dist[i].len = city[S][i].len;
        dist[i].fees = city[S][i].fees;
    }
    int V;                  //用來表示頂點下標
    while(1){
        V = findMinDist();
        if(V == -1)     //這樣結點不存在
            break;
        flag[V] = 1;    //吃入
        for(int i = 0; i < N; ++i){ //對圖中的每個頂點
            if(flag[i] == 0 && city[V][i].len < INFINITY){  // W是V的鄰邊且未被吃入
                if(city[V][i].len < 0) //為負邊
                    return ;    //不能正確處理，返回錯誤標記
                if(dist[V].len + city[V][i].len < dist[i].len){ //吃入V使得dist[i]變小
                    dist[i].len = dist[V].len + city[V][i].len;
                    dist[i].fees = dist[V].fees + city[V][i].fees;
                }else if(dist[V].len + city[V][i].len == dist[i].len){ //吃入V等於dist[i]
                    if(dist[V].fees + city[V][i].fees < dist[i].fees)   //路費比其少則更新
                        dist[i].fees = dist[V].fees + city[V][i].fees;
                }

            }
        }
    }
}

int main(void){
    scanf("%d%d%d%d", &N, &M, &S, &D);
    init(); //初始化
    int beginCity;
    int endCity;
    int len;
    int fees;
    for(int i = 0; i < M; ++i){
        scanf("%d%d%d%d", &beginCity, &endCity, &len, &fees);
        city[beginCity][endCity].len = len;
        city[beginCity][endCity].fees = fees;
        city[endCity][beginCity].len = len;
        city[endCity][beginCity].fees = fees;
    }
    dijkstra();
//    for(int i = 0 ; i < N; ++i)
//        printf("i=%d len=%d fees=%d\n", i, dist[i].len, dist[i].fees);
    printf("%d %d", dist[D].len, dist[D].fees);

    return 0;
}