參考書目：《數值分析》 

y=x*x-a求零點 用零點附近(這裡起始取的a/2,因為牛頓迭代左右均收斂，所以不會出現迭代發散的狀況)拋物線切線與x軸所截的交點，在以交點做拋物線的切線繼續求交點，進而不斷迭代來近似拋物線的零點 由於該函式在零點附近是收斂的(二階收斂)所以能不斷迭代。而對於y=x*x*x-a函式則不一定行，如果a大於0，會存在三個根，對於第二個根，牛頓迭代則不會收斂。以後補上matlab影象。最終推匯出迭代公式x1=(x0+a/x0)/2。

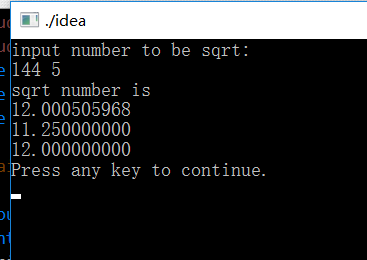
測試結果如下：

可以看出牛頓迭代速度遠遠快於二分求根

//main函式入口

#include <stdio.h>
#include <math.h>
double sqrt1(double a,int tot);
double sqrt2(double a,int tot);
double sqrt3(double a,int tot);


int main(void)
{
double i;
int j;
printf("input number to be sqrt:\n");
scanf("%lf %d",&i,&j);
printf("sqrt number is \n%.9f \n%.9f \n%.9f",sqrt1(i,j),sqrt2(i,j),sqrt3(i,1E-10));
return 0;
}

double sqrt1(double a,int tot)//傳入二分迭代次數
{
	double x,y;
	int i;
	x=a/2;
	for(i=0;i<tot;i++)
	{
		y=(x+a/x)/2;
		x=y;
	}
	return y;
}
double sqrt2(double a,int tot)
{
	int i;
	double low,mid,high;
	low=0;
	high=a>1?a:1;  //避免在0到1之間的因變數超過自變數的區間
	mid=(low+high)/2;
	for(i=0;mid*mid!=a&&i<tot;i++)//如果直接相等退出迴圈
	{
		if(mid*mid<a)
		{
			low=mid;
			mid=(low+high)/2;
		}
		else
		{
			high=mid;
			mid=(low+high)/2;
		}
	}
	return mid;
}
double sqrt3(double a,int err) //傳入誤差限
{
	double x,y,temp;
	temp=a/2;
	do{
		x=temp; //temp保留中間結果 方便x,y的比較
		temp=(x+a/x)/2;
		y=temp;
	}while(fabs(x-y)>err);
	return y;
}