以HDU_1542 Atlantis 題為例

線段樹和掃描線是這麼結合的

    線段樹統計的是有效區間段的長度 也就是掃描線 當前掃描到的區間段是哪一個
    什麼意思 比如當前在哪一個段掃描 那麼線段樹中的t[1]中的len就是多長
    線段樹一般情況下是一個後序遍歷先把孩子節點的資訊 更新後 再拿孩子節點的資訊回來更新自己

    一旦取消這個線段 遇到了出邊 那麼就把這個點的覆蓋情況置空 然後讓這個點的資訊為左右兩個孩子的資訊 統計
    如果這個時候左右兩個孩子還有邊的資訊 那麼依然會反饋回來 如果沒有 那麼這個線段就會置零


    總的來說 線段樹統計的就是當前掃描時段真正的有效長度是多少
    如何通過線段樹去統計？
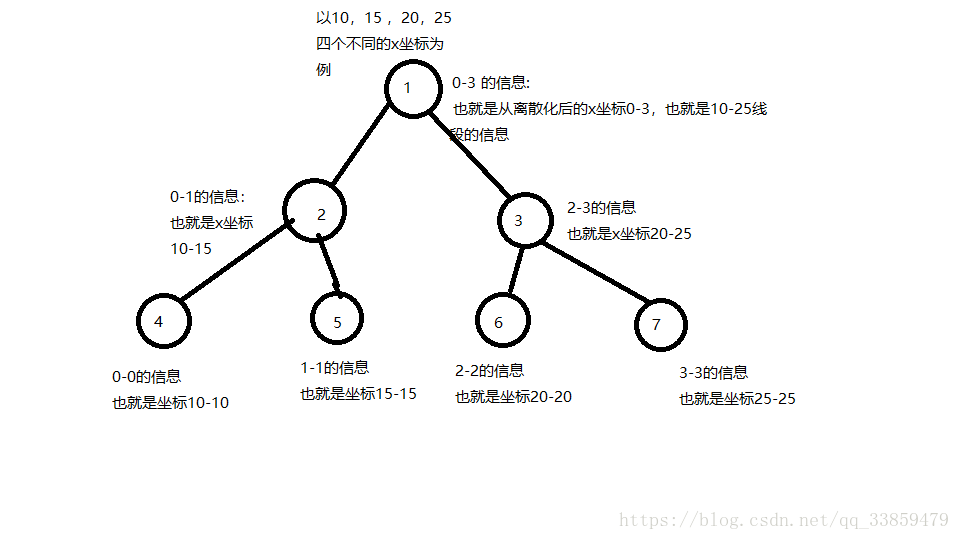
    以離散化橫座標為例
    線段樹每個葉子節點統計的都是我們所有出現過的從小到大的離散化後的x座標順序下標
    比如一共出現了10 15 20 25四個x座標 由於我們離散化的是橫座標 也就是要拿橫座標建樹
    也就是這四個點分別對應0 1 2 3 四個點
    把線段樹建成了
    那麼每次我們掃描到一個線段 就到線段樹中去更新這個線段
    什麼意思？ 就是按照這個線段是出邊還是入邊
    如果是矩形入邊 那麼就把這個線段拿到線段樹中去 我們不是已經把線段樹按照對應x左邊建好了嗎
    那麼現在遇到一個入邊 按照我們之前說的線段樹需要維護的東西————“當前掃描的線段所在的矩形的有效寬度”
    我們需要讓線段樹明白現在的有效寬度是不是變化了
    也就是把這個變得起始座標 結束座標搞下來 更新到線段樹中
    這樣我們到時候一查線段樹的有效寬度 然後再用高度做一下差
    就知道當前掃描矩形的有效面積是多少了
    那麼我們拿到當前邊的兩個座標 去線段樹中更新
    如果這個區間段線上段樹中沒有標記過 那麼就去標記
    標記後反饋給父節點
    不斷的反饋 最後父節點得到了當前狀態下的有效寬度

    那麼如果當前邊是個出邊 也就是有可能需要減少

    依然是拿到線段樹中 把寬度取消

    當我們遍歷了掃描方向上的所有的邊 也就是把每一塊的面積都累加了起來 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 110;
struct node{
    int xx;
    double len;
    int l,r;
}t[maxn<<3];
double x[maxn<<2];
int xtot;
struct edge{
    double l,r,h;
    int xx;
    edge(){}
    edge(double a,double b,double c,int cover):l(a),r(b),h(c),xx(cover){}
    bool operator<(const edge &E){
        return h<E.h;
    }
}e[maxn<<2];
int etot;
bool cmp(int a,int b){
    return a<b;
}
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
void build(int l,int r,int rt){
    t[rt].l = l;
    t[rt].r = r;
    t[rt].xx = t[rt].len = 0;
    if(l==r)return;
    int mid = l+r>>1;
    build(lson);
    build(rson);
}
void pushup(int now){
    if(t[now].xx){
        t[now].len = x[t[now].r+1]-x[t[now].l];
    }
    else if(t[now].l==t[now].r){
        t[now].len=0;
    }
    else {
        t[now].len = t[now<<1].len+t[now<<1|1].len;
    }
}

void update(int l,int r,int rt,int val){
    if(t[rt].l==l&&t[rt].r==r){
        t[rt].xx += val;
        pushup(rt);
        return;
    }
    int mid = t[rt].l+t[rt].r>>1;//*****
    if(r<=mid)update(l,r,rt<<1,val);
    else if(l>mid)update(l,r,rt<<1|1,val);
    else{
        update(l,mid,rt<<1,val);
        update(mid+1,r,rt<<1|1,val);
    }
    pushup(rt);
}
int main()
{
    int n,test=0;
    while(scanf("%d",&n),n){
        double x1,x2,y1,y2;
        test++;
        for(int i=1;i<=n;i++){
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            e[etot++] = edge(x1,x2,y1,1);
            e[etot++] = edge(x1,x2,y2,-1);
            x[xtot++] = x1;
            x[xtot++] = x2;
        }
        sort(e,e+etot);
        sort(x,x+xtot);
        xtot = unique(x,x+xtot)-x;//離散化x座標
        double ans =0;
        build(0,xtot-1,1);
        for(int i=0;i<etot;i++){
            int l = lower_bound(x,x+xtot,e[i].l)-x;
            int r = lower_bound(x,x+xtot,e[i].r)-x-1;
            //區間這裡並不是完全包含比如10，15，20，25 的區間 查詢10-15 那麼去查的就是10-10
            //什麼意思 因為線段樹仍然是離散的統計結構 仍然還是按照起點查詢區間線段
            update(l,r,1,e[i].xx);
            ans+=(e[i+1].h-e[i].h)*t[1].len;
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",test,ans);
        etot = 0;
        xtot = 0;
    }
    return 0;

}