大數同餘定理
阿新 • • 發佈:2019-02-15
(a+b)%c=(a%c+b%c)%c
#include <iostream> #include <cstdio> #include <cmath> #include <cstring> using namespace std; char a[1000]; int n,i; int main() { while (~scanf("%s%d",a,&n)) { int m=0; int l=strlen(a); for (i=0;i<l;i++) m=((m*10)%n+(a[i]-'0'))%n; cout<<m<<endl; } return 0; }
數學上,當兩個整數除以同一個正整數,若得相同餘數,則二整數同餘。同餘理論常被用於數論中。最先引用同餘的概念與“≡”符號者為德國數學家高斯。
同餘符號
兩個整數 ,
, ,若它們除以正整數
,若它們除以正整數 所得的餘數相等,則稱
所得的餘數相等,則稱 ,
, 對於模
對於模 同餘
同餘
記作
讀作 同餘於
同餘於 模
模 ,或讀作
,或讀作 與
與 關於模
關於模 同餘。
同餘。
比如 。
。
同餘於的符號是同餘相等符號 ≡。統一碼值為 U+2261。但因為方便理由,人們有時會把它(誤)寫為普通等號 (=)。
整除性
 (即是說
a 和 b 之差是 m 的倍數)
(即是說
a 和 b 之差是 m 的倍數)
換句話說,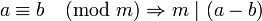 [注
1]
[注
1]
傳遞性

保持基本運算
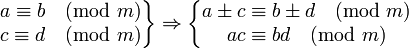
這性質更可進一步引申成為這樣:
除法原理
尤拉定理
主條目:尤拉定理
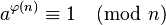
威爾遜定理
主條目:威爾遜定理

整除多項式
例子
- 求自然數a的個位數字,就是求a與哪一個數對於模10同餘。


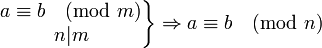

![\left. \begin{matrix} a \equiv b \pmod{m_1} \\ a \equiv b \pmod{m_2} \\ \vdots \\ a \equiv b \pmod{m_n} \\ (n \ge 2) \end{matrix} \right\} \Rightarrow a \equiv b \pmod{[m_1,m_2,\cdots,m_n]}](https://upload.wikimedia.org/math/7/a/c/7ac195605b5ea5cc8dc46b95e1e8f4b2.png)
 ,而
,而 整除
整除
 。
。 表示
m 能
表示
m 能 表示
表示 的
的![[m_1,m_2,\cdots,m_n]](https://upload.wikimedia.org/math/2/b/d/2bde71a774b734d1861784b91da73f91.png) 表示
表示