c++ 正整數拆分成素因子的乘積
阿新 • • 發佈:2019-02-16
#include<string>
//設計演算法,將某個大於1的數分成素因子的乘積 6=2*3 7=7 8=2*2*2
//1.判斷當前數是不是素數,是直接返回
//2.否則,迴圈直到第一個它能整除的素數,當前數變為除以素數後的商,繼續大迴圈。
//判斷一個數是不是素數
#include <math.h>
bool isPrime(int x){
if (x <= 1)
return false;
if (x == 2)
return true;
if (x % 2 == 0)
return false;
int tmax = (int)sqrt(x) + 1; //sqrt(9)返回的是浮點數,有可能是2.9999或3.00001等,確保正確性,多比較一次
int i = 3;
while (i < tmax){
if (x%i == 0)
return false;
i+=2;
}
return true;
}
string primeMulti(int x){
string s = "";
s+= to_string(x)+"=";
while (x != 1){
if (isPrime(x)){
s =s+ to_string(x);
return s;
}
if (x % 2 == 0){
s += "2*";
x /= 2;
}
for (int i = 3; i <= x; i += 2){
if (isPrime(i) && x%i == 0){
s += to_string(i) + "*";
x /= i;
break;
}
}
}
if (x == 1) //若最終x為1,需去掉尾上多餘的乘號
s = s.substr(0,s.size()-1);
return s;
}
改進:先把小於該數的素數求出來,儲存在vector中,可以減少素數的重複判斷
#include <iostream> #include <string> #include <vector> #include <math.h> using namespace std; bool isPrime(long n){ if (n <= 1) return false; else if (n == 2) return true; else if (n % 2 == 0) return false; else{ int maxsqr = (long)sqrt(n) + 1; for (long i = 3; i<maxsqr; i = i + 2){ if (n%i == 0) return false; } } return true; } void prime(long n, vector<long>& vec){ if (n <= 1) return; for (long i = 2; i <= n; ++i){ if (isPrime(i)) vec.push_back(i); } return; } int main(){ vector<long> v = {}; long n; cin >> n; prime(n, v); while (n != 1){ long i = 0; while (v[i] <= n){ if (n%v[i] == 0){ cout << v[i] << " "; n = n / v[i]; break; } ++i; } } cout << endl; return 0; }
發現一個更簡單的,不用判斷是不是素數,直接除以比n小的數即可。
void primeFactor(long n){
if(n<=1)
return;
while(n!=1){
for(int i=2;i<=n;++i){
if(n%i==0){
cout << i << " ";
n=n/i;
break;
}
}
}
}加一個其它習題:
//設計演算法,求二項式c(n,k)的係數 //c(n,k)=c(n,k-1)+c(n-1,k-1) int er(int n,int k){ if (k == 0 || k==n) return 1; if (k > n / 2) k = n - k; return er(n- 1, k) + er(n - 1, k - 1); }
再加一個漢諾塔問題,都是用遞迴實現的。遞迴可以讓程式碼更簡潔,甚至解決一些迴圈不能解決或解決起來超級複雜的問題
void move(int n,char from, char to){
cout <<n<<":"<< from << "->" << to << endl;
}
//實現漢諾塔盤子移動
//關鍵點:只有一個盤子,直接把它從from移動到to,否則,先移動n-1個盤子,以to為臨時柱子
//移動到tmp;再移動第n個盤子到to;最後將那n-1個盤子從tmp以from為臨時柱子移動到to
void hanuota(int n, char from, char tmp, char to){
if (n == 1)
move(n,from, to);
else{
hanuota(n - 1, from, to, tmp);
move(n,from, to);
hanuota(n - 1, tmp, from, to);
}
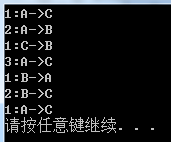
}執行hanuota(3,'A','B','C');得到的輸出: