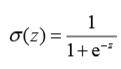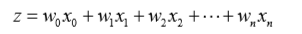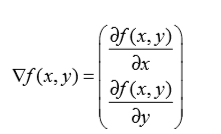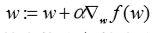什麼是迴歸？

假設現在有一些資料點，我們用一條直線對這些點進行擬合（該線稱為最佳擬合直線），這個擬合過程就稱作迴歸。

涉及到迴歸問題，我們藉助Sigmoid函式來處理，Sigmoid函式：

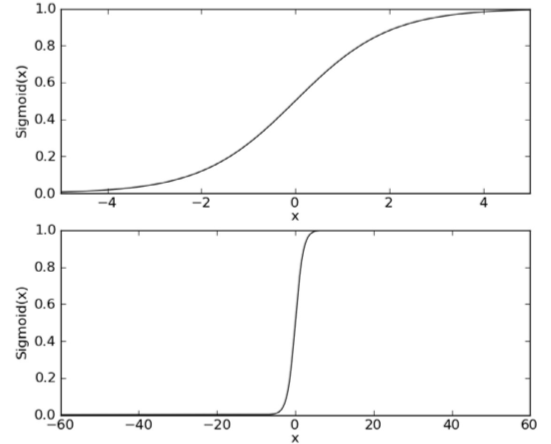
x=0時，函式值是0.5，x越大函式值越趨近於1，x越小函式值越趨近於0。

如果x的刻度足夠大Sigmoid函式也可以堪稱一個單位階躍函式。之所以採用Sigmoid來解決迴歸問題，是因為在一定條件下Sigmoid函式呈現出“線性”的特性，“線性”的體現就是迴歸係數。

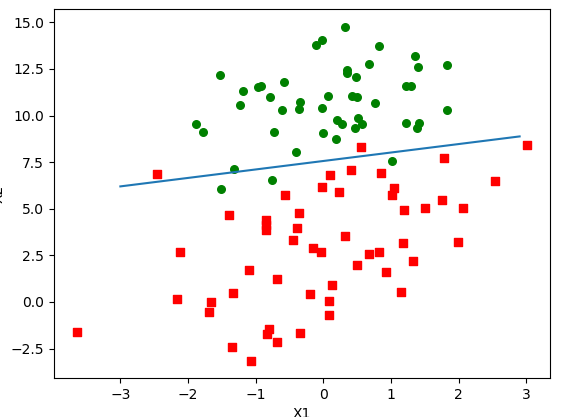
先來解釋Sigmoid的線性，Sigmoid函式的輸入記為z，假設有n個特性，也就是說有n個向量，那麼Sigmoid函式中入參z可以標識成：

小寫的w是各個向量上的迴歸係數，小寫的x是各個向量上的入參。

如果採用向量的寫法，上述公式可以寫成z = WX，大寫的W是多向量的迴歸係數，大寫的X是多向量的一套入參。

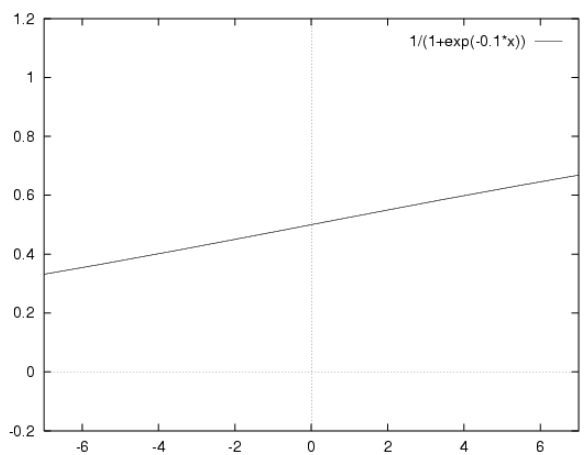
從公式中我們可以看出只要W是非零值，Z最終都會趨於無窮大和無窮小，所以Sigmoid函式值終將趨於0和1；但是如果W足夠小，那麼X在一定範圍內對Z的影響將會放緩，相當於將上面第一張圖向X軸兩邊拉長了，那麼在一定範圍內就會趨向與一條直線，也就是說會變成線性的。例如W=0.1時，x在(-7,7)之間的圖形是這樣的：

理解了線性之後後面的問題就變得簡單了，我們對多向量的資料集進行0、1分組時就演化成了了求Z的過程，也就是求多向量的迴歸係數

在求得W的過程中採用的是梯度上升演算法，梯度上升法基於的思想是：要找到某函式的最大值，最好的方法是沿著該函式的梯度方向探尋。如果梯度記為∇，則函式f(x,y)的梯度表示為：

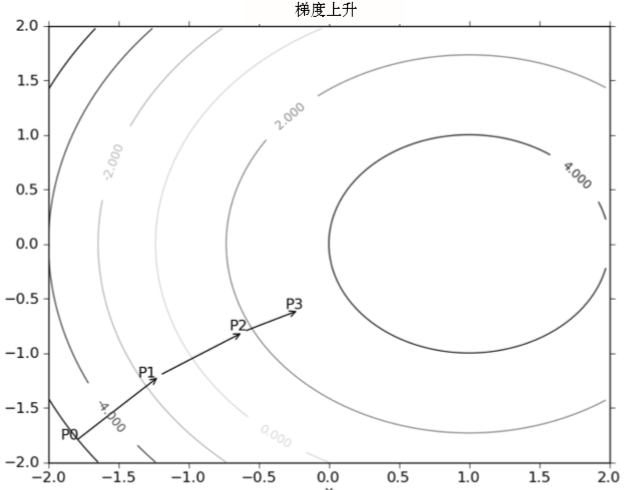
梯度上升演算法到達每個點後都會重新估計移動的方向。從P0開始，計算完該點的梯度，函式就根據梯度移動到下一點P1。在P1點，梯度再次被重新計算，並沿新的梯度方向移動到P2。如此迴圈迭代，直到滿足停止條件。迭代的過程中，梯度運算元總是保證我們能選取到最佳的移動方向

梯度上升演算法，每上升一步，梯度運算元總是指向函式值增長最快的方向，這裡用的是方向而不是移動量的大小，是因為需要引入一個“步長”α的概念，步長越長，每次向山頂移動的越快，但是精準度越低，α的平衡是個學問。

梯度上升就是個不斷遞迴的過程，每移動一步，更新當前的結果，重新計算剩下的最優方向，用公式標識是：

PS：梯度上升法如爬山一樣，是求山頂最大值的方法，與梯度上升法對應的是梯度下降法，是求最小值的方法，將公式中的+號改成-號既可。

有了上面的理論基礎，我們開始用程式碼和樣例來演練下，訓練檔案在git上https://github.com/yejingtao/forblog/blob/master/MachineLearning/trainingSet/testSet.txt，格式如下：

-0.017612	14.053064	0

-1.395634	4.662541	1

-0.752157	6.538620	0

-1.322371	7.152853	0

0.423363	11.054677	0

0.406704	7.067335	1

0.667394	12.741452	0

其中前兩項為特性，最後一列為結果。

要做的事情簡單來說就是繪製一條“直線”，將圖中這些訓練集劃分為兩部分，處理這種0、1分類的場景我們採用前面介紹的Sigmoid函式，而求“直線”的過程就是求W的過程。

準備演示的訓練集和結果集：

#載入訓練集和結果集
def loadDataSet() :
    dataMat = []
    labelMat = []
    fr = open('C:\\2017\\提高\\機器學習\\訓練樣本\\testSet.txt')
    for line in fr.readlines():
        lineArray = line.strip().split()
        #這裡給第一向量設定了1.0值，因為從分佈圖中看得出不是過原點的直線，所以要最終的W中要有x位的偏移量
        dataMat.append([1.0,float(lineArray[0]), float(lineArray[1])])
        labelMat.append(int(lineArray[2]))
    return dataMat,labelMat

#sigmoid函式
def sigmoid(inX) :
    return 1.0/(1.0+exp(-inX))


#最終返回的weights可以理解為梯度的塔頂
def gradAscent(dataMatIn, classLabels) :
    dataMatrix = mat(dataMatIn)
    #transpose將行陣列轉成列向量
    labelMatrix = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    # 返回的是步長alpha，訓練次數maxCycle的迴歸係數
    alpha = 0.001
    maxCycle = 500
    weights = ones((n,1))
    for i in range(maxCycle) :
        #h是一個列向量
        h = sigmoid(dataMatrix * weights)
        #列向量相減，得到的還是個列向量error
        error = labelMatrix - h
        #dataMatrix.transpose()*error是矩陣相乘，事實上該運算包含了300次的乘積
        #梯度上升，對weights做修正
        weights = weights+alpha * dataMatrix.transpose()*error
    #返回也是個列向量
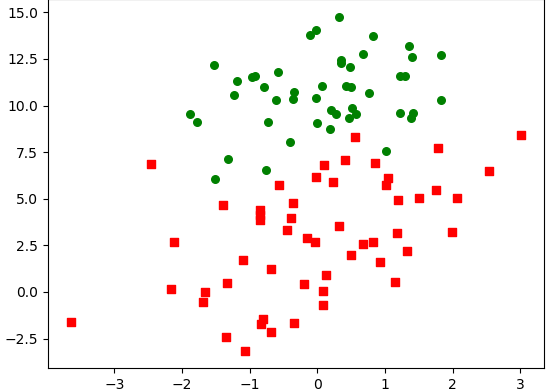
    return weights

利用matplotlib模組用影象來驗證迴歸係數：

def plotBestFit(wei) :
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xc1=[]
    yc1=[]
    xc2=[]
    yc2=[]
    for i in range(n) :
        if int(labelMat[i])==1 :
            xc1.append(dataArr[i,1])
            yc1.append(dataArr[i,2])
        else :
            xc2.append(dataArr[i, 1])
            yc2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xc1,yc1,s=30,c='red',marker='s')
    ax.scatter(xc2, yc2, s=30, c='green')
    x = arange(-3.0,3.0,0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

測試程式碼：

dataMat,labelMat = loadDataSet()
weights = gradAscent(dataMat,labelMat)
print(weights)
plotBestFit(weights)

這裡有一行程式碼不容易理解需要解釋下：y = (-weights[0]-weights[1]*x)/weights[2]，來自：

公式中x0=常量1，x1=這裡的x，x2=這裡的y，同時z取0，是因為在z=0時Sigmoid函式值為1/2正好是0與1的臨界點。

所以從0= weights[0]*1+ weights[1]*x + weights[2]*y推導而來。

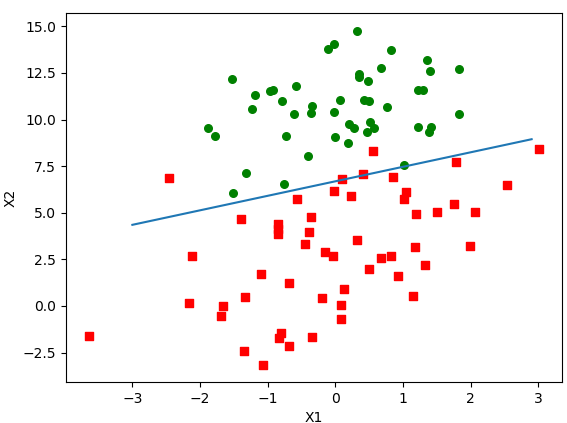
從影象結果來看回歸係數比較理想，但是缺點也很明顯，儘管例子簡單且資料集很小，這個方法卻需要大量的計算量。

假設我們的資料集是幾萬幾億 的話，該訓練演算法計算量將不可控制

再介紹下隨機梯度上升法：

def stocGradAscent0 (dataMatrix, classLabels) :
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m) :
        h = sigmoid(sum(dataMatrix[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha*error*dataMatrix[i]
    return weights

測試結果是：[ 1.017020070.85914348 -0.36579921]

一個判斷優化演算法優劣的可靠方法是看它是否收斂，也就是說引數是否達到了穩定值，是否還會不斷地變化。可以看到目前結果並沒有收斂，假如繼續不斷對隨機梯度進行遞迴的話，最終將會收斂，這裡請看下機器學習實踐中給出的測試結果：

X0和X1要迭代很久才能收斂，X2很快就可以收斂，X1和X2存在一定的波動，波動來源於趨於臨界點的資料，在n次修訂後在n+1次又被修訂回去，重複資料的來回修訂引起了波動。

基於以上的分析我們對隨機梯度上升法進行加強，第一如何最快收斂，第二如何減少波動。

1調整步長儘快收斂，開始時步長設定較大，減少前期計算上的浪費，越是趨於收斂時步長越小

2隨機資料減少波動，前面已經分析過既然重複資料的來回修訂引起了波動，那麼我們就採用隨機資料來訓練演算法。

加強後的程式碼是:

def stocGradAscent1 (dataMatrix, classLabels, numIter=150) :
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter) :
        dataIndex = list(range(m))
        for i in range(m) :
            #動態的步長，i，j越大越趨於穩定，步長越小
            alpha = 4/(1.0+i+j) + 0.01
            #隨機訓練入參解決波動問題
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha*error*dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

測試結果：

[ 14.565233880.87521806-1.92639734]

雖然迴歸係數不如基本梯度上升法優秀，但是該演算法是考慮到了計算量和迴歸性的平衡。

Logistic迴歸

優點：計算代價不高，易於理解和實現。

缺點：容易欠擬合，分類精度可能不高。

適用資料型別：數值型和標稱型資料。