這裡講一下我對偏序集的認識   如果有偏差可以評論我  我會修改

一：定義 （度娘上copy來的  不想看的可以跳過

設R是非空集合A上的一個二元關係，若R滿足： 自反性、反對稱性、傳遞性，則稱R為A上的偏序關係。

以下為定義：
非嚴格偏序，自反偏序
給定集合S，“≤”是S上的二元關係，若“≤”滿足：
自反性：∀a∈S，有a≤a；
反對稱性：∀a，b∈S，a≤b且b≤a，則a=b；
傳遞性：∀a，b，c∈S，a≤b且b≤c，則a≤c；
則稱“≤”是S上的非嚴格偏序或自反偏序。
嚴格偏序，反自反偏序
給定集合S，“<”是S上的二元關係，若“<”滿足：
反自反性：∀a∈S，有a≮a；
非對稱性：∀a，b∈S，a<b ⇒ b≮a；
傳遞性：∀a，b，c∈S，a<b且b<c，則a<c；
則稱“<”是S上的嚴格偏序或反自反偏序。
嚴格偏序與有向無環圖(dag)有直接的對應關係。一個集合上的嚴格偏序的關係圖就是一個有向無環圖。其傳遞閉包是它自己。
下面是一些主要的例子[1]  :
自然數的集合配備了它的自然次序(小於等於關係)。這個偏序是全序。
整數的集合配備了它的自然次序。這個偏序是全序。
自然數的集合的有限子集 {1, 2, ..., n}。這個偏序是全序。
自然數的集合配備了整除關係。
給定集合的子集的集合(它的冪集)按包含排序。
向量空間的子空間的集合按包含來排序。
一般的說偏序集合的兩個元素 x 和 y 可以處於四個相互排斥的關聯中任何一個: 要麼 x < y，要麼 x = y，要麼 x > y，
要麼 x 和 y 是“不可比較”的(三個都不是)。全序集合是用規則排除第四種可能的集合: 所有元素對都是可比較的，
並且聲稱三分法成立。自然數、整數、有理數和實數都關於它們代數(有符號)大小是全序的，而複數不是。這不是說複數不能全序排序；
比如我們可以按詞典次序排序它們，通過 x+iy < u+iv 當且僅當 x < u 或 (x = u 且 y < v)，
但是這種排序沒有合理的大小意義因為它使得 1 大於 100i。按絕對大小排序它們產生在其中所有對都是可比較的預序，
但這不是偏序因為 1 和 i 有相同的絕對大小但卻不相等，違反了反對稱性。


在數學中，特別是序理論中，是指配備了偏序關係的集合。
這個關係形式化了排序、順序或排列這個集合的元素的直覺概念。
這種排序不必然需要是全部的，就是說不需要但也可以保證在這個集合內的所有物件的相互可比較性。(在數學用法中，全序是一種偏序)。
偏序集合定義了偏序拓撲

看到這裡很多人會一頭霧水   因為純數學的表達太生澀了   那麼我就舉一個例子

              建立一個二元組(x,y)中的偏序集

             (x1,y1)<=(x2,y2)當且僅當 x1<=x2  與 y1<=y2同時成立

            則集合{(x,y) |x,y∈R }中任選兩個元素  (i,j)   (k,l)  不一定有 (i,j)<=(k,l) 或 (k,l)<=(i,j)

            這就是一個偏序集

             偏序集中的元素可以任意推廣，但是必須有偏序關係

好了   現在你應該對偏序集有一些認識了吧

          特別的在R中當偏序關係為<=時，任選元素a,b   必有 a<=b 或 b <= a那麼我們 稱這是一個全序集

二    偏序集中的概念

        鏈                  :    D 中的一個子集 C   滿足 C 是全序集  及C中所有元素都可以比較大小

        反鏈              :    D 中的一個子集 B   滿足 B 中任意非空子集都不是全序集  即所有元素之間都不可以比較大小

        鏈覆蓋          :    若干個鏈的並集為 D ，且兩兩之間交集為 ∅ 

        反鏈覆蓋      :    若干個反鏈的並集為 D ，且兩兩之間交集為∅

        最長鏈          :    所有鏈中元素個數最多的  (可以有多個最長鏈)

        最長反鏈      :    所有反鏈中元素個數最多的 (可以有多個最長反鏈

        偏序集高度  :    最長鏈的元素個數

        偏序集寬度  :    最長反鏈中的元素個數

三  Dilworth定理

         最小鏈覆蓋（使鏈最少）= 最長反鏈長度 = 偏序集寬度 

         最小反鏈覆蓋=最長鏈長度=偏序集深度

現在我們看到BZOJ 1143

        題意很明顯  是要求圖中的最長反鏈長度  x<=y即為x可以到y   我們可以用Floyd預處理偏序關係

        之後我們可以構造一個二分圖 對於一個點x  我們用  x1 x2分別表示它在鏈中關係

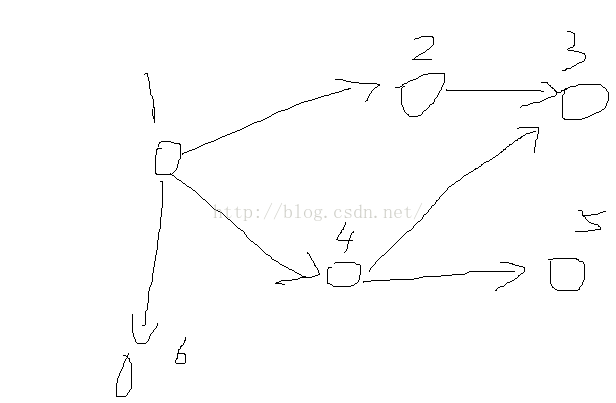
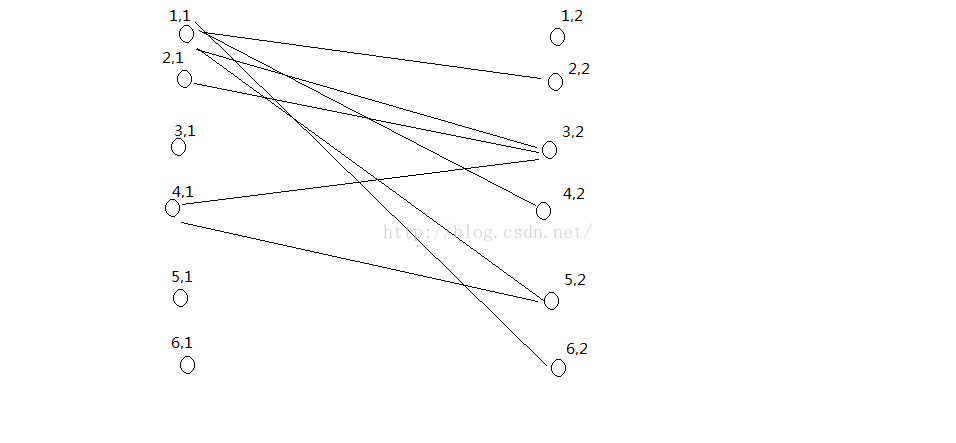
           若 x<=y 則建立(x1,y2)這一條邊(不理解這個過程可以見下圖)

這個是原圖   然後構造二分圖

顯然 有N個點  二分圖中的最大匹配為A   原圖最小鏈覆蓋為B

         有N-A=B

如果不懂的話可以看我的證明(可能很不嚴謹

            若二分圖記憶體在增廣路徑(x1,y2)  則  x1   y2都沒有連邊   x為一條鏈的末尾   y為一條鏈的開始  又有 x<=y  所以當前的覆蓋不是原圖的最小鏈覆蓋

那麼對於這一題思路就已經講完了   複雜度是O(n^3)的