超能粒子炮 · 改

t組詢問,求\(\sum_{i=0}^kC_n^imod\ 2333\)。

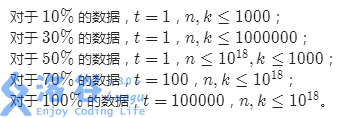
解

不難得知2333為質數，考慮lucus定理，設yyb為模數，於是我們有

\[ans=\sum_{i=0}^kC_{n/yyb}^{i/yyb}C_{n\%yyb}^{i\%yyb}\]

註意到整除形式，考慮整除分塊，對單個整除的值考慮

\[ans=C_{n/yyb}^{0}\sum_{i=0}^{yyb-1}C_{n\%yyb}^i+C_{n/yyb}^{1}\sum_{i=0}^{yyb-1}C_{n\%yyb}^i+...+\]

\[C_{n/yyb}^{k/yyb-1}\sum_{i=0}^{yyb-1}C_{n\%yyb}^i+C_{n/yyb}^{k/yyb}\sum_{i=0}^{k\%yyb}C_{n\%yyb}^i=\]

\[\sum_{i=0}^{k/yyb-1}C_{n/yyb}^i*\sum_{i=0}^{yyb-1}C_{n\%yyb}^i+C_{n/yyb}^{k/yyb}\sum_{i=0}^{k\%yyb}C_{n\%yyb}^i\]

於是設\(f[n][m]\)表示\(\sum_{i=0}^nC_m^i\),故原式可以被表示為

\[ans=f[k/yyb-1][n/yyb]f[yyb-1][n\%yyb]+C_{n/yyb}^{k/yyb}f[k\%yyb][n\%yyb]\]

以此遞歸處理，額外lucus定理處理式子剩下的組合數。

參考代碼：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define ll long long
#define yyb 2333
using namespace std;
int jc[yyb],jv[yyb],tr[yyb][yyb];
il void prepare();
il int pow(int,int),C(int,int),
    lucus(ll,ll),ddc(ll,ll);
int main(){
    int t;ll n,k;
    scanf("%d",&t),prepare();
    while(t--)scanf("%lld%lld",&n,&k),
                  printf("%d\n",ddc(n,k));
    return 0;
}
il int ddc(ll n,ll r){
    if(r<0)return 0;if(!n||!r)return 1;
    return (ddc(n/yyb,r/yyb-1)*tr[n%yyb][yyb-1]%yyb
        +lucus(n/yyb,r/yyb)*tr[n%yyb][r%yyb]%yyb)%yyb;
}
il int lucus(ll n,ll r){
    int ans(1);
    while(r)ans=ans*C(n%yyb,r%yyb)%yyb,
                n/=yyb,r/=yyb;return ans;
}
il int pow(int x,int y){
    int ans(1);
    while(y){
        if(y&1)ans=ans*x%yyb;
        x=x*x%yyb,y>>=1;
    }return ans;
}
il int C(int n,int r){
    if(n<r)return 0;
    return jc[n]*jv[r]%yyb*jv[n-r]%yyb;
}
il void prepare(){
    int i,j;
    for(i=jc[0]=jv[0]=1;i<yyb;++i)
        jc[i]=jc[i-1]*i%yyb;
    --i,jv[i]=pow(jc[i],yyb-2);
    while(i>1)jv[i-1]=jv[i]*i%yyb,--i;
    for(i=0;i<yyb;++i)
        for(j=tr[i][0]=1;j<yyb;++j)
            tr[i][j]=(tr[i][j-1]+C(i,j))%yyb;
}
 

超能粒子炮 · 改