Side Window Filtering 論文解讀和C++實現
剛開始看到這篇論文的時候,我就很感興趣想去復現一把看看效果。
這篇論文是今年 CVPR oral 且不是深度學習方向的,其核心貢獻點就是:
不管原來的濾波器保不保邊,運用了side-window思想之後,都可以讓它變成保邊濾波!
於是利用業餘時間,參考作者開源的matlab程式碼,我用C++實現了一下Side-window
盒子濾波,其他濾波器有時間再試下,下面是github的連結,讀者可以去跑下程式碼看看效果玩下,
從實驗結果上看我覺得算是復現了論文的效果:
https://github.com/Ldpe2G/ArmNeonOptimization/tree/master/sideWindowBoxFilter
我們來看下復現論文的效果,對於一張普通圖片,經典的盒子濾波和side-window
盒子濾波的效果對比:

從濾波結果對比上可以看到,經典的盒子濾波隨著對同一張圖片反覆應用盒子濾波的迭代次數
的增加,視覺效果是越來越模糊,到了30次迭代的時候已經糊的沒法看了,但是Side-window
盒子濾波即使迭代了30次,對於邊緣的保持還很好,和原圖基本看不出大的區別,就是邊緣細節
有些丟失。然後對原圖加上椒鹽噪聲,再對比下濾波效果:

從濾波結果對比上可以看到,經典的盒子濾波到了10次迭代的時候,雖然椒鹽噪聲已經很好
的消除了,但是圖片也變得很模糊,邊緣都細節都丟失了,但是Side-window盒子濾波卻能
很好的消除椒鹽噪聲的同時,對於邊緣的保持還很好,基本上算是還原了原圖。
下面從我的理解上去簡單解讀下這篇論文的核心思想,還有我在復現過程中的一些實現
細節介紹。目前的經典濾波演算法基本都是,以某個畫素點為中心,按照濾波半徑,把這個
包括畫素點和其領域加權組合得到輸出,一般公式如下:
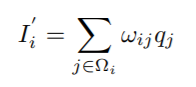
Ω是以畫素點 i 為中心的濾波視窗,w是濾波權值,q是原影象素值,I'是輸出結果。
但是這樣以一個畫素為中心去濾波會的問題在於,如果一個畫素點處在邊緣位置
(這裡的邊緣不是指圖片的大小邊界,而是指影象中物體的邊緣)的話,以畫素為
中心的濾波會導致濾波結果的邊緣部分變模糊。具體是為什麼,論文中給出了分析過程。
首先來看下,論文中的一張圖:
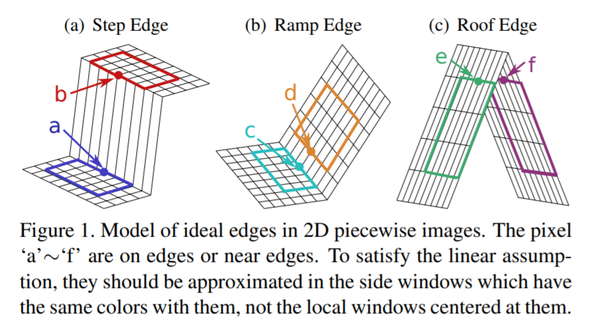
文中提到為了分析方便只討論3種典型的邊緣,分別是圖中的
(a)階梯狀邊緣、(b)斜坡狀邊緣和(c)屋頂狀邊緣。論文中也給出了這3三種邊緣的形象展示:

然後文中採用了泰勒展開去分析,首先假定,影象上(x, y)座標點的畫素值為g(x, y),對於
圖中展示的情況來看,函式 g(x, y)是連續但不可導的。對於(a)階梯狀邊緣的 'a' (藍色方框那個店)
點來說,文中定義 'a-' 和 'a+' 來分別表示 'a' 點左極限 (x - ε, y),和右極限 (x + ε, y)。且 ε > 0。
很明顯從圖中可以看出來 g(x - ε, y) ≠ g(x + ε, y) 且/或(文中的用詞是"and (or)")
g'(x - ε, y) ≠ g'(x + ε, y),導數也不等由於邊緣部分的跳躍。因此對於這兩塊區域的泰勒展開也是
不一樣的,首先來看下泰勒展開的一般公式:
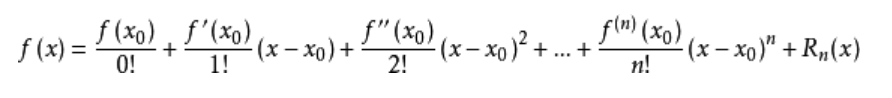
“泰勒公式是將一個在 x=x0 處具有n階導數的函式 f(x) 利用關於 (x - x0) 的n次多項式來
逼近函式的方法。”----百度百科
根據文中的分析,這裡設定 f(x) = g(x - 2ε, y),x0 = x - ε,則根據泰勒展開公式:
g(x - 2ε, y) ≈ f(x0) + f'(x0)(x - x0)
= g(x - ε, y) + g'(x - ε, y)(x - 2ε - (x - ε))
= g(x - ε, y) + g'(x - ε, y)(- ε)
同理,設 f(x) = g(x + 2ε, y),x0 = x + ε,則泰勒展開得:
g(x + 2ε, y) ≈ f(x0) + f'(x0)(x - x0)
= g(x + ε, y) + g'(x + ε, y)(x + 2ε - (x + ε))
= g(x + ε, y) + g'(x + ε, y)ε
所以從兩邊的泰勒展開式可以得出結論,對於 'a-' 區域的濾波估計肯定是來自區域 'a' 的左邊,
而對於 'a-' 估計是來自於 'a' 的右邊,然後類比分析區域 'b','c' 和 'd' 都可以得到類似的結論。
因此分析得到的結論是,如果一個畫素點處於影象中的邊緣位置,那麼濾波的時候就應該把
濾波器的邊緣和該畫素點對齊,而不是把濾波器的中心和該畫素點對齊。受該發現的啟發,
文中提出了一個新的保邊濾波策略,就是把每個濾波畫素點都當成是潛在的邊緣點,然後
對於每個待濾波的畫素點,生成幾種不同的濾波子視窗,然後把這些濾波視窗的邊緣或者
角點位置和該畫素點對齊,然後濾波得到結果,最後根據把這些子視窗的濾波之後的最佳
重構結果作為最終的濾波結果。以上就是side window 濾波的思想。
然後文中提出了8個方向的濾波視窗,分別是上、下,左、右、左上、右上、左下和右下。
還有對於視窗的分析,最後就可以得到side window filter的核心演算法流程:

然後論文中又詳細分析了 box filter 和 side window box filter 對於上面提到的三種經典
邊緣的濾波之後的保留情況。文中給出分析的圖表如下:
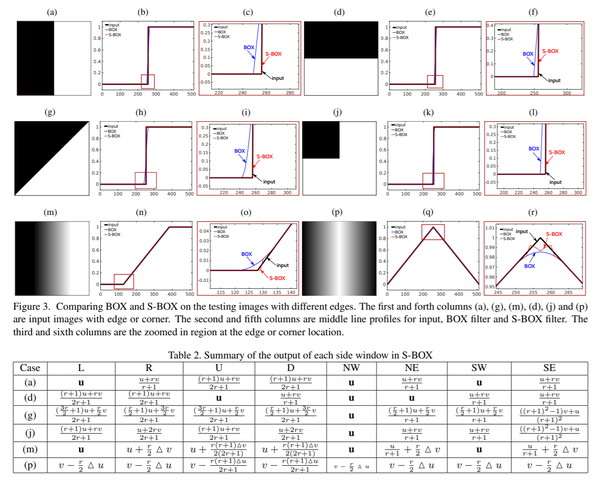
總的來說結論就是 side window box filter 對於階梯和斜坡狀的邊緣都能完整的保留,
而對於屋頂狀邊緣雖然不能完整的保留邊緣,但是也比經典的盒子濾波要好很多。
在復現過程中,本來一開始是想對文中提到的8種side window去分別寫對應的盒子濾波的,
因為盒子濾波有個經典的優化思路,可以讓執行時間不受濾波半徑的影響,
具體可以參考我之前寫得一篇部落格:
移動端arm cpu優化學習筆記----一步步優化盒子濾波(Box Filter)
後來仔細想了下,這8個side window其實也就是邊界處理不同,核心運算邏輯都是一致的,
最後就是抽象成一個函式,對於不同的side window傳不同的邊界引數,
就不需要每個視窗寫一個函數了,具體可以看看github上的程式碼。
最後看看一組結果,看看在迭代10次的情況下,經典box filter 和 side window box filter的結果對比:

熊貓寶寶原圖

濾波結果, box filter, iteration = 10

濾波結果, side window box filter, iteration = 10

熊貓寶寶原圖+椒鹽噪聲

去噪結果, box filter, iteration = 10

去噪結果, side window box filter, iteration = 10
相關資料:
