今天，發生一件非常有趣的事情。

公司同事問了我一個問題：為什麼 2.0 - 1.1 = 0.89999999 呢？不應該是 0.9嗎？

原來是，他問了周圍一圈的同事，都給他的是同一個回答，說這是精度問題。他百思不得其解，怎麼就會產生精度問題呢。再問，就沒人知道原因了。

然後，我就看到了他抱著一本厚厚的書在看。拿過來一看，是一本Java書，厚厚的六百多頁，這還僅是第一卷。喲呵，這是準備大幹一場啊。

看在他這麼努力學習的份上，還有他那對知識極度渴望的眼神。我決定，把我畢生所學傳授與他。

於是，就給他詳細講解了，計算機中是怎麼儲存一個數的，十進位制是怎麼在轉二進位制的過程中丟失精度的，以及浮點數是怎麼遵循IEEE 754 規範的，在浮點數進行加減運算的過程中會經歷對階、移位運算等過程，以及在此過程中是怎麼丟失精度的。（這些問題在之前的文章中都有解答，參看“為什麼0.1+0.2=0.30000000000000004”）

然後，成功的把他徹底搞懵逼了。怎麼這麼難啊。

原來，他的計算機基礎比我還匱乏，不知道什麼是位運算，不知道什麼是原碼、反碼和補碼。

本著我的熱心腸，我就給他普及了一下這些知識 ---- 負數的補碼形式和位移運算。

我們知道，一個數分為有符號和無符號。對於，有符號的數來說，最高位代表符號位，即最高位1代表負數，0代表正數。

在計算機中，儲存一個數的時候，都是以補碼的形式儲存的。而正數和負數的補碼錶示方式是不一樣的。正數的補碼就等於它的原碼，而負數的補碼是原碼除符號位以外都取反，然後 + 1 得來的。以一個int型別為例（4個位元組即32位）

14的原碼為：

0000 0000 0000 0000 0000 0000 0000 1110

它的反碼、補碼和原碼都是一樣的。

-14的原碼為:

//最高位1為符號位，代表此數為負數
1000 0000 0000 0000 0000 0000 0000 1110

反碼為原碼除了符號位以外的其他位都取反（即0變為1，1變為0），

1111 1111 1111 1111 1111 1111 1111 0001

補碼為反碼 + 1 ，注意二進位制中是滿二進一。

1111 1111 1111 1111 1111 1111 1111 0010

位的左移，右移運算就是分別向左和向右移動N位。移位的規則是：

1. 不管有沒有符號位，左移都是在低位補0
2. 帶符號右移，是在高位補符號位，即正數補0，負數補1
3. 無符號右移，無論該數是正數還是負數都在高位補0

因左移就在右邊低位補0就可以了，比較簡單，我就以負數的右移來舉例，是怎麼計算無符號右移和帶符號右移的。還是以 -14 為例。

// -14的補碼
1111 1111 1111 1111 1111 1111 1111 0010
// 帶符號右移用 >> 表示，即右移一位 -14>>1，高位補符號位1，低位捨去
1111 1111 1111 1111 1111 1111 1111 1001
// 無符號右移用 >>> 表示，即右移一位 -14>>>1，最高位補0
0111 1111 1111 1111 1111 1111 1111 1001

我們可以通過程式來驗證一下 -14>>1和 -14>>>1的結果是否正確。

1. -14>>1 = -7

//我們算出來 -14>>1的補碼為：
1111 1111 1111 1111 1111 1111 1111 1001
//那它具體代表的數值是多少呢？
//首先，補碼 -1 得到反碼
1111 1111 1111 1111 1111 1111 1111 1000
//然後，反碼取反得到原碼，最高位符號位不變
1000 0000 0000 0000 0000 0000 0000 0111

這結果不就是 -7 嗎，然後通過程式計算一下結果：

public class TestMove {
    public static void main(String[] args) {
        System.out.println( -14>>1);
    }
}

結果同樣也是-7 。說明了我們位移操作沒問題。

2. -14>>>1=2147483641

我們通過一段程式去驗證：

package com.test.binary;
​
/**
 * @Author zwb
 * @DATE 2019/12/3 15:49
 */
public class TestBinary {
    public static void main(String[] args) {
        //我們自己計算出來的 -14>>>1 結果
        String bin = "01111111111111111111111111111001";
        double res = binToDec(bin);
        System.out.println(res);
        //通過計算機計算的結果
        System.out.println(-14>>>1);
    }
​
    //二進位制轉為十進位制
    public static double binToDec(String bin){
        int index = bin.indexOf(".");
        int len = bin.length();
        double res = 0;
        //index為-1說明沒有小數
        if(index == -1){
            for(int i = 0; i< len; i++){
                res += Math.pow(2,i) * Integer.parseInt(String.valueOf(bin.charAt(len-1-i)));
            }
        }else{
            //整數部分
            int partA = 0;
            for(int i = 0; i< index; i++){
                partA += Math.pow(2,i) * Integer.parseInt(String.valueOf(bin.charAt(index-1-i)));
            }
            //小數部分
            double partB = 0;
            for(int j = index + 1; j < len; j++){
                partB += Math.pow(2,index - j) * Integer.parseInt(String.valueOf(bin.charAt(j)));
            }
            res = partA + partB;
        }
        return res;
    }
}

執行之後的結果，可以在控制檯列印看到：

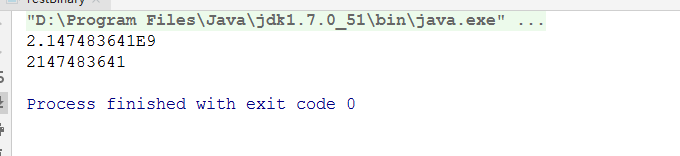
上邊第一個是我們自己通過推算它的補碼，然後通過二進位制轉十進位制的一個演算法算出來的最終結果，第二個就是直接通過位運算算出來的結果。可以看到結果是一模一樣的。

至此，是不是對原碼，反碼，補碼以及位運算左移右移，有了比較清晰的認識了呢？