從頭學pytorch(四) softmax迴歸實現
阿新 • • 發佈:2019-12-26
FashionMNIST資料集共70000個樣本,60000個train,10000個test.共計10種類別.

通過如下方式下載.
mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor())
softmax從零實現
- 資料載入
- 初始化模型引數
- 模型定義
- 損失函式定義
- 優化器定義
- 訓練
資料載入
import torch import torchvision import torchvision.transforms as transforms mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=True, download=True, transform=transforms.ToTensor()) mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST', train=False, download=True, transform=transforms.ToTensor()) batch_size = 256 num_workers = 4 # 多程序同時讀取 train_iter = torch.utils.data.DataLoader( mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers) test_iter = torch.utils.data.DataLoader( mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
初始化模型引數
num_inputs = 784 # 影象是28 X 28的影象,共784個特徵
num_outputs = 10
W = torch.tensor(np.random.normal(
0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)模型定義
記憶要點:沿著dim方向.行為維度0,列為維度1. 沿著列的方向相加,即對每一行的元素相加.
def softmax(X): # X.shape=[樣本數,類別數]
X_exp = X.exp()
partion = X_exp.sum(dim=1, keepdim=True) # 沿著列方向求和,即對每一行求和
#print(partion.shape)
return X_exp/partion # 廣播機制,partion被擴充套件成與X_exp同shape的,對應位置元素做除法
def net(X):
# 通過`view`函式將每張原始影象改成長度為`num_inputs`的向量
return softmax(torch.mm(X.view(-1, num_inputs), W) + b)損失函式定義
假設訓練資料集的樣本數為\(n\),交叉熵損失函式定義為
\[\ell(\boldsymbol{\Theta}) = \frac{1}{n} \sum_{i=1}^n H\left(\boldsymbol y^{(i)}, \boldsymbol {\hat y}^{(i)}\right ),\]
其中\(\boldsymbol{\Theta}\)代表模型引數。同樣地,如果每個樣本只有一個標籤,那麼交叉熵損失可以簡寫成\(\ell(\boldsymbol{\Theta}) = -(1/n) \sum_{i=1}^n \log \hat y_{y^{(i)}}^{(i)}\)。
def cross_entropy(y_hat, y):
y_hat_prob = y_hat.gather(1, y.view(-1, 1)) # ,沿著列方向,即選取出每一行下標為y的元素
return -torch.log(y_hat_prob)https://pytorch.org/docs/stable/torch.html
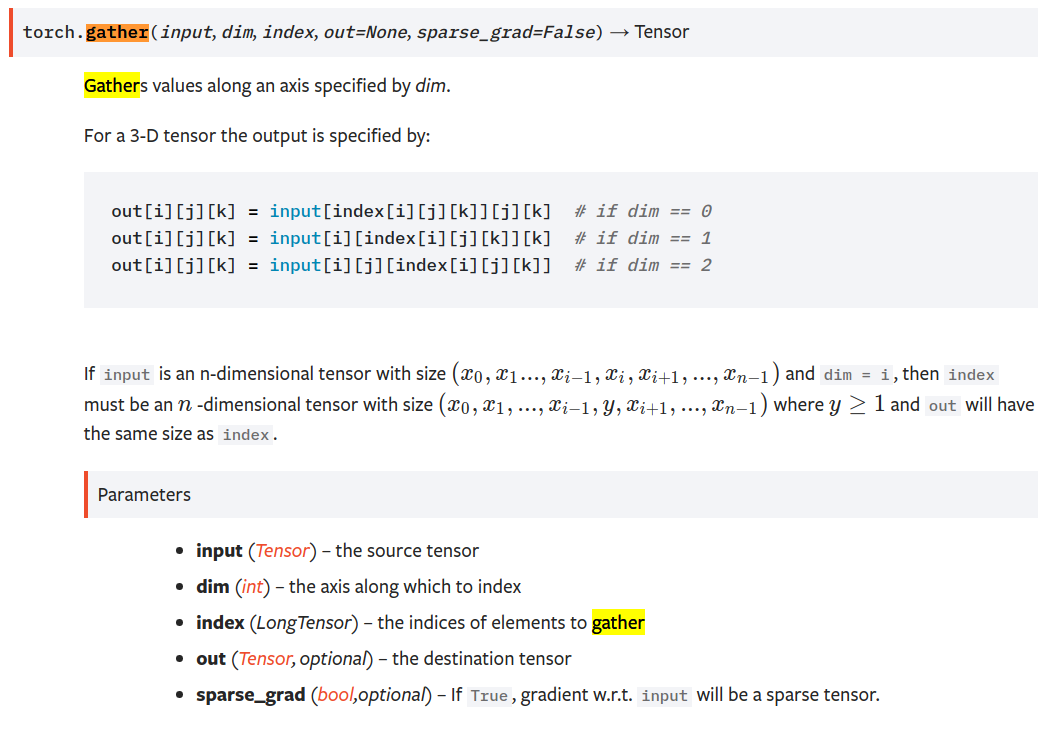
gather()沿著維度dim,選取索引為index的元素
優化演算法定義
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意這裡更改param時用的param.data準確度評估函式
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n訓練
- 讀入batch_size個樣本
- 前向傳播,計算預測值
- 與真值相比,計算loss
- 反向傳播,計算梯度
- 更新各個引數
如此迴圈往復.
num_epochs, lr = 5, 0.1
def train():
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
#print(X.shape,y.shape)
y_hat = net(X)
l = cross_entropy(y_hat, y).sum() # 求loss
l.backward() # 反向傳播,計算梯度
sgd([W, b], lr, batch_size) # 根據梯度,更新引數
W.grad.data.zero_() # 清空梯度
b.grad.data.zero_()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train_acc %.3f,test_acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum/n, test_acc))
train()輸出如下:
epoch 1, loss 0.7848, train_acc 0.748,test_acc 0.793
epoch 2, loss 0.5704, train_acc 0.813,test_acc 0.811
epoch 3, loss 0.5249, train_acc 0.825,test_acc 0.821
epoch 4, loss 0.5011, train_acc 0.832,test_acc 0.821
epoch 5, loss 0.4861, train_acc 0.837,test_acc 0.829-------
softmax的簡潔實現
- 資料載入
- 模型定義及初始化模型引數
- 損失函式定義
- 優化器定義
- 訓練
資料讀取
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
import torchvision
import torchvision.transforms as transforms
mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
train=True, download=True,
transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
train=False, download=True,
transform=transforms.ToTensor())
batch_size = 256
num_workers = 4 # 多程序同時讀取
train_iter = torch.utils.data.DataLoader(
mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(
mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)模型定義及模型引數初始化
num_inputs = 784 # 影象是28 X 28的影象,共784個特徵
num_outputs = 10
class LinearNet(nn.Module):
def __init__(self,num_inputs,num_outputs):
super(LinearNet,self).__init__()
self.linear = nn.Linear(num_inputs,num_outputs)
def forward(self,x): #x.shape=(batch,1,28,28)
return self.linear(x.view(x.shape[0],-1)) #輸入shape應該是[,784]
net = LinearNet(num_inputs,num_outputs)
torch.nn.init.normal_(net.linear.weight,mean=0,std=0.01)
torch.nn.init.constant_(net.linear.bias,val=0)沒有什麼要特別注意的,注意一點,由於self.linear的input size為[,784],所以要對x做一次變形x.view(x.shape[0],-1)
損失函式定義
torch裡的這個損失函式是包括了softmax計算概率和交叉熵計算的.
loss = nn.CrossEntropyLoss()優化器定義
optimizer = torch.optim.SGD(net.parameters(),lr=0.01)訓練
精度評測函式
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n訓練
- 讀入batch_size個樣本
- 前向傳播,計算預測值
- 與真值相比,計算loss
- 反向傳播,計算梯度
- 更新各個引數
如此迴圈往復.
num_epochs = 5
def train():
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X,y in train_iter:
y_hat=net(X) #前向傳播
l = loss(y_hat,y).sum()#計算loss
l.backward()#反向傳播
optimizer.step()#引數更新
optimizer.zero_grad()#清空梯度
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train()輸出
epoch 1, loss 0.0054, train acc 0.638, test acc 0.681
epoch 2, loss 0.0036, train acc 0.716, test acc 0.724
epoch 3, loss 0.0031, train acc 0.749, test acc 0.745
epoch 4, loss 0.0029, train acc 0.767, test acc 0.759
epoch 5, loss 0.0028, train acc 0.780, test acc 0.770
