從頭學pytorch(三) 線性迴歸
關於什麼是線性迴歸,不多做介紹了.可以參考我以前的部落格https://www.cnblogs.com/sdu20112013/p/10186516.html
實現線性迴歸
分為以下幾個部分:
- 生成資料集
- 讀取資料
- 初始化模型引數
- 定義模型
- 定義損失函式
- 定義優化演算法
- 訓練模型
生成資料集
我們構造一個簡單的人工訓練資料集,它可以使我們能夠直觀比較學到的引數和真實的模型引數的區別。設訓練資料集樣本數為1000,輸入個數(特徵數)為2。給定隨機生成的批量樣本特徵 \(\boldsymbol{X} \in \mathbb{R}^{1000 \times 2}\),我們使用線性迴歸模型真實權重 \(\boldsymbol{w} = [2, -3.4]^\top\) 和偏差 \(b = 4.2\),以及一個隨機噪聲項 \(\epsilon\) 來生成標籤
其中噪聲項 \(\epsilon\) 服從均值為0、標準差為0.01的正態分佈。噪聲代表了資料集中無意義的干擾。
%matplotlib inline import torch from IPython import display from matplotlib import pyplot as plt import numpy as np import random num_inputs = 2 num_examples = 1000 true_w = [2, -3.4] true_b = 4.2 features = torch.from_numpy(np.random.normal(0, 1, (num_examples, num_inputs))) print(type(features),features.shape) labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b print(type(labels),labels.shape) labels += torch.from_numpy(np.random.normal(0, 0.01, size=labels.size())) def use_svg_display(): # 用向量圖顯示 display.set_matplotlib_formats('svg') def set_figsize(figsize=(3.5, 2.5)): use_svg_display() # 設定圖的尺寸 plt.rcParams['figure.figsize'] = figsize set_figsize() plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);
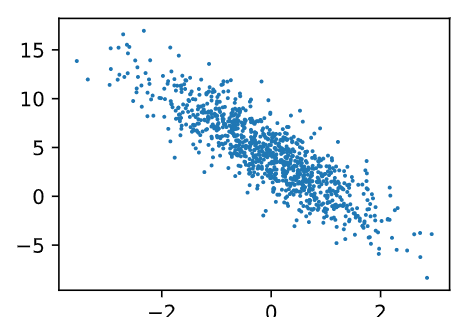
讀取資料
每次讀取batch_size個樣本.注意亂序讀取.以使得每個batch的樣本多樣性足夠豐富.
def data_iter(batch_size, features, labels): num_examples = len(features) #print(num_examples) indices = list(range(num_examples)) random.shuffle(indices) # 樣本的讀取順序是隨機的 #print(indices) for i in range(0, num_examples, batch_size): j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最後一次可能不足一個batch #print(j) yield features.index_select(0, j), labels.index_select(0, j) batch_size = 10 for X, y in data_iter(batch_size, features, labels): #print(X, y) #break pass
關於yiled用法參考:https://www.cnblogs.com/sdu20112013/p/11216584.html中yield部分.
關於torch的index_select用法參考:https://pytorch-cn.readthedocs.io/zh/latest/package_references/torch/#torchindex_select

features是[1000,2]的Tensor。所以features.index_select(0, j)即在第0維度上對索引為j的輸入進行切片.也即選取第j(j為一個長度為batch_size的tensor)個樣本.
初始化模型引數
權重值有2個.所以我們初始化一個shape為[2,1]的Tensor.我們將其隨機初始化為符合均值0,標準差0.01的正態分佈隨機數,bias初始化為0.
w=torch.from_numpy(np.random.normal(0,0.01,(num_inputs,1)))
b = torch.zeros(1, dtype=torch.float64)
print(w.dtype,b.dtype)ndarray的型別是float64,所以w的型別是float64,在生成b的時候我們指定dtype=float64.
之後的模型訓練中,需要對這些引數求梯度來迭代引數的值,因此我們要讓它們的requires_grad=True。
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True) 定義模型
下面是線性迴歸的向量計算表示式的實現。我們使用mm函式做矩陣乘法。
在我們的例子中,X是[1000,2]的矩陣,w是[2,1]的矩陣,相乘得到[1000,1]的矩陣.
def linreg(X, w, b): # 本函式已儲存在d2lzh_pytorch包中方便以後使用
return torch.mm(X, w) + b定義損失函式
我們使用平方損失來定義線性迴歸的損失函式。在實現中,我們需要把真實值y變形成預測值y_hat的形狀。以下函式返回的結果也將和y_hat的形狀相同。
def squared_loss(y_hat, y):
# 注意這裡返回的是向量, 另外, pytorch裡的MSELoss並沒有除以 2
return (y_hat - y.view(y_hat.size())) ** 2 / 2定義優化演算法
以下的sgd函式實現了上一節中介紹的小批量隨機梯度下降演算法。它通過不斷迭代模型引數來優化損失函式。這裡自動求梯度模組計算得來的梯度是一個批量樣本的梯度和。我們將它除以批量大小來得到平均值。均值反映了平均而言,對單個樣本,朝著哪個梯度方向去更新引數可以使得loss最小
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意這裡更改param時用的param.data這裡的params傳入的即w,b
訓練模型
我們建立一個迴圈,每次傳入batch_size個樣本,計算損失.反向傳播,計算w,b的梯度,然後更新w,b.迴圈往復.注意每次方向傳播後清空梯度. 以及l是一個向量. 呼叫.sum()將其轉換為標量,再計算梯度.
一個epoch即所有樣本均計算一次損失.
程式碼如下:
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
batch_size=10
for epoch in range(num_epochs):
for X,y in data_iter(batch_size,features,labels):
l = loss(linreg(X,w,b),y).sum()
l.backward()
sgd([w,b],lr,batch_size)
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features,w,b),labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
print(true_w,'\n',w)
print(true_b,'\n',b)輸出如下:
epoch 1, loss 0.051109
epoch 2, loss 0.000217
epoch 3, loss 0.000049
[2, -3.4]
tensor([[ 1.9996],
[-3.3993]], dtype=torch.float64, requires_grad=True)
4.2
tensor([4.1995], dtype=torch.float64, requires_grad=True)可以看到得到的w和b都已經非常接近true_w,true_b了.
之前我們是手寫程式碼構建模型,建立損失函式,定義隨機梯度下降等等.用pytorch裡提供的類和函式,可以更方便地實現線性迴歸.
線性迴歸的簡潔實現
生成資料集
與前面沒有區別.
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.from_numpy(np.random.normal(0, 1, (num_examples, num_inputs)))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.from_numpy(np.random.normal(0, 0.01, size=labels.size()))資料讀取
用torch.utils.data模組,主要使用TensorDataset類和DataLoader類
import torch.utils.data as Data
batch_size=10
dataset = Data.TensorDataset(features,labels)
data_iter = Data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
for X,y in data_iter:
print(X,y)
break建立網路結構
在上一節從零開始的實現中,我們需要定義模型引數,並使用它們一步步描述模型是怎樣計算的。當模型結構變得更復雜時,這些步驟將變得更繁瑣。其實,PyTorch提供了大量預定義的層,這使我們只需關注使用哪些層來構造模型。下面將介紹如何使用PyTorch更簡潔地定義線性迴歸。
首先,匯入torch.nn模組。實際上,“nn”是neural networks(神經網路)的縮寫。顧名思義,該模組定義了大量神經網路的層。之前我們已經用過了autograd,而nn就是利用autograd來定義模型。nn的核心資料結構是Module,它是一個抽象概念,既可以表示神經網路中的某個層(layer),也可以表示一個包含很多層的神經網路。在實際使用中,最常見的做法是繼承nn.Module,撰寫自己的網路/層。一個nn.Module例項應該包含一些層以及返回輸出的前向傳播(forward)方法。下面先來看看如何用nn.Module實現一個線性迴歸模型。
class LinearNet(nn.Module):
def __init__(self, n_feature):
super(LinearNet, self).__init__()
self.linear = nn.Linear(n_feature, 1)
# forward 定義前向傳播
def forward(self, x):
y = self.linear(x)
return y
net = LinearNet(num_inputs)
print(net) # 使用print可以打印出網路的結構輸出:
LinearNet(
(linear): Linear(in_features=2, out_features=1, bias=True)
)事實上我們還可以用nn.Sequential來更加方便地搭建網路,Sequential是一個有序的容器,網路層將按照在傳入Sequential的順序依次被新增到計算圖中。
# 寫法一
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此處還可以傳入其他層
)
# 寫法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 寫法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
('linear', nn.Linear(num_inputs, 1))
# ......
]))
print(net)
print(net[0])輸出:
Sequential(
(linear): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)可以通過net.parameters()來檢視模型所有的可學習引數,此函式將返回一個生成器。
for param in net.parameters():
print(param)輸出:
Parameter containing:
tensor([[-0.2956, -0.2817]], requires_grad=True)
Parameter containing:
tensor([-0.1443], requires_grad=True)作為一個單層神經網路,線性迴歸輸出層中的神經元和輸入層中各個輸入完全連線。因此,線性迴歸的輸出層又叫全連線層。
注意:
torch.nn僅支援輸入一個batch的樣本不支援單個樣本輸入,如果只有單個樣本,可使用input.unsqueeze(0)來新增一維。
初始化模型引數
在使用net前,我們需要初始化模型引數,如線性迴歸模型中的權重和偏差。PyTorch在init模組中提供了多種引數初始化方法。這裡的init是initializer的縮寫形式。我們通過init.normal_將權重引數每個元素初始化為隨機取樣於均值為0、標準差為0.01的正態分佈。偏差會初始化為零。
from torch.nn import init
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0) # 也可以直接修改bias的data: net[0].bias.data.fill_(0)定義優化演算法
同樣,我們也無須自己實現小批量隨機梯度下降演算法。torch.optim模組提供了很多常用的優化演算法比如SGD、Adam和RMSProp等。下面我們建立一個用於優化net所有引數的優化器例項,並指定學習率為0.03的小批量隨機梯度下降(SGD)為優化演算法。
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)輸出:
SGD (
Parameter Group 0
dampening: 0
lr: 0.03
momentum: 0
nesterov: False
weight_decay: 0
)我們還可以為不同子網路設定不同的學習率,這在finetune時經常用到。例:
optimizer =optim.SGD([
# 如果對某個引數不指定學習率,就使用最外層的預設學習率
{'params': net.subnet1.parameters()}, # lr=0.03
{'params': net.subnet2.parameters(), 'lr': 0.01}
], lr=0.03)有時候我們不想讓學習率固定成一個常數,那如何調整學習率呢?主要有兩種做法。
- 一種是修改
optimizer.param_groups中對應的學習率
# 調整學習率
for param_group in optimizer.param_groups:
param_group['lr'] *= 0.1 # 學習率為之前的0.1倍- 另一種是更簡單也是較為推薦的做法——新建優化器,由於optimizer十分輕量級,構建開銷很小,故而可以構建新的optimizer。但是後者對於使用動量的優化器(如Adam),會丟失動量等狀態資訊,可能會造成損失函式的收斂出現震盪等情況。
訓練
所有的optimizer都實現了step()方法,這個方法會更新所有的引數。它能按兩種方式來使用:
- optimizer.step()
這是大多數optimizer所支援的簡化版本。一旦梯度被如backward()之類的函式計算好後,我們就可以呼叫這個函式。
for input, target in dataset:
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()- optimizer.step(closure)
一些優化演算法例如Conjugate Gradient和LBFGS需要重複多次計算函式,因此你需要傳入一個閉包去允許它們重新計算你的模型。這個閉包應當清空梯度, 計算損失,然後返回。
for input, target in dataset:
def closure():
optimizer.zero_grad()
output = model(input)
loss = loss_fn(output, target)
loss.backward()
return loss
optimizer.step(closure)具體參考https://pytorch-cn.readthedocs.io/zh/latest/package_references/torch-optim/
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零,等價於net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))
dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)輸出:
epoch 1, loss: 0.000227
epoch 2, loss: 0.000160
epoch 3, loss: 0.000136
[2, -3.4] Parameter containing:
tensor([[ 2.0007, -3.4010]], requires_grad=True)
4.2 Parameter containing:
tensor([4.1998], requires_grad=True)總結:
- 使用PyTorch可以更簡潔地實現模型。
torch.utils.data模組提供了有關資料處理的工具,torch.nn模組定義了大量神經網路的層,torch.nn.init模組定義了各種初始化方法,torch.optim模組提供了模型引數優化的各種方法。
