從頭學pytorch(十五):AlexNet
AlexNet
AlexNet是2012年提出的一個模型,並且贏得了ImageNet影象識別挑戰賽的冠軍.首次證明了由計算機自動學習到的特徵可以超越手工設計的特徵,對計算機視覺的研究有著極其重要的意義.
AlexNet的設計思路和LeNet是非常類似的.不同點主要有以下幾點:
- 啟用函式由sigmoid改為Relu
- AlexNet使用了dropout,LeNet沒有使用
- AlexNet引入了大量的影象增廣,如翻轉、裁剪和顏色變化,從而進一步擴大資料集來緩解過擬合
啟用函式
relu
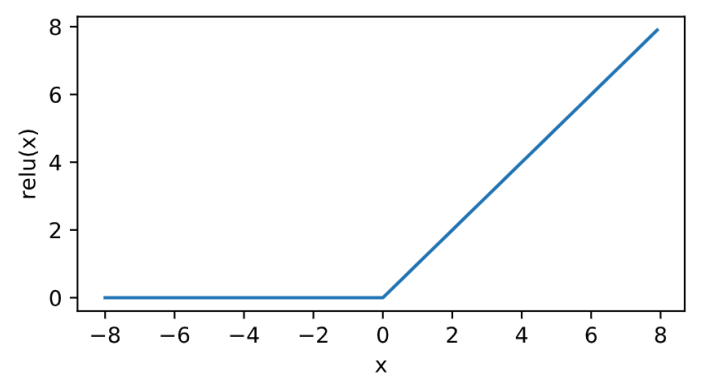
\[\text{ReLU}(x) = \max(x, 0).\]
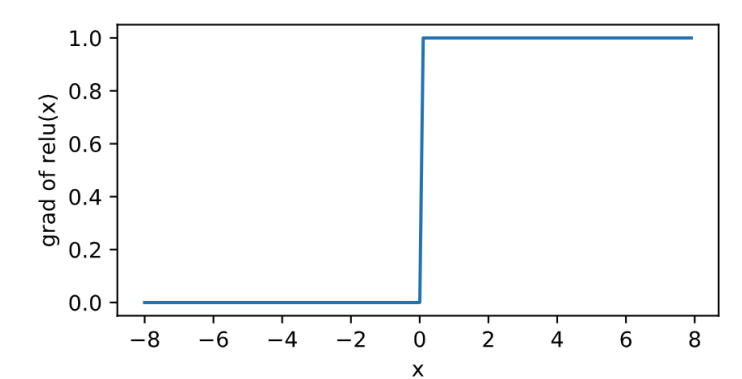
其曲線及導數的曲線圖繪製如下:
sigmoid
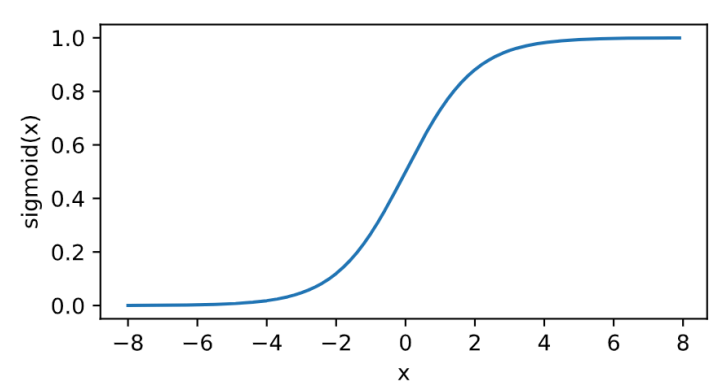
其曲線及導數的曲線圖繪製如下:
\[\text{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.\]
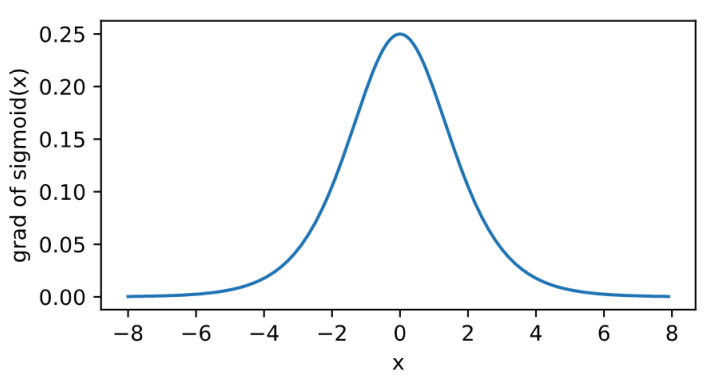
relu的好處主要有兩點:
- 計算更簡單,沒有了指數運算
- 在正數區間,梯度恆定為1,而sigmoid在接近0和1時,梯度幾乎為0,會導致模型引數更新極為緩慢
現在大多模型啟用函式都選擇Relu了.
模型結構
AlexNet結構如下:

早期的硬體裝置計算能力不足,所以上面的圖分成了兩部分,把不同部分的計算分散到不同的gpu上去,現在已經完全沒有這種必要了.比如第一個卷積層的channel是48 x 2 = 96個.
根據上圖,我們來寫模型的定義:
首先,用一個11 x 11的卷積核,對224 x 224的輸入,卷積後得到55 x 55 x 96的輸出.
nn.Conv2d(1, 96, kernel_size=11, stride=4)然而,我們測試一下他的輸出.
X=torch.randn((1,1,224,224)) #batch x c x h x w
net = nn.Conv2d(1, 96, kernel_size=11, stride=4)
out = net(X)
print(out.shape)輸出
torch.Size([1, 96, 54, 54])我們將程式碼修改為
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2)
再用相同的程式碼測試輸出
X=torch.randn((1,1,224,224)) #batch x c x h x w
net = nn.Conv2d(1, 96, kernel_size=11, stride=4,padding=2)
out = net(X)
print(out.shape)輸出
torch.Size([1, 96, 55, 55])由此可見,第一個卷積層的實現應該是
nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2)搜尋pytorch的padding策略,https://blog.csdn.net/g11d111/article/details/82665265基本都是抄這篇的,這篇裡指出
顯然,padding=1的效果是:原來的輸入層基礎上,上下左右各補了一行!
然而實測和文章中的描述不一致.
net = nn.Conv2d(1, 1, 3,padding=0)
X= torch.randn((1,1,5,5))
print(X)
out=net(X)
print(out)
net2 = nn.Conv2d(1, 1, 3,padding=1)
out=net(X)
print(out)輸出
tensor([[[[-2.3052, 0.7220, 0.3106, 0.0605, -0.8304],
[-0.0831, 0.0168, -0.9227, 2.2891, 0.6738],
[-0.7871, -0.2234, -0.2356, 0.2500, 0.8389],
[ 0.7070, 1.1909, 0.2963, -0.7580, 0.1535],
[ 1.0306, -1.1829, 3.1201, 1.0544, 0.3521]]]])
tensor([[[[-0.1129, 0.7711, -0.6452],
[-0.3387, 0.1025, 0.3039],
[ 0.1604, 0.2709, 0.0740]]]], grad_fn=<MkldnnConvolutionBackward>)
tensor([[[[-0.1129, 0.7711, -0.6452],
[-0.3387, 0.1025, 0.3039],
[ 0.1604, 0.2709, 0.0740]]]], grad_fn=<MkldnnConvolutionBackward>)到目前,我也沒有把torch的padding策略搞清楚.知道的同學請評論留言.我的torch版本是1.2.0
AlexNet的啟用函式採用的是Relu,所以
nn.ReLU(inplace=True)接下來用一個3 x 3的卷積核去做最大池化,步幅為2,得到[27,27,96]的輸出
nn.MaxPool2d(kernel_size=3, stride=2)我們測試一下:
X=torch.randn((1,1,224,224)) #batch x c x h x w
net = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4,padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2)
)
out = net(X)
print(out.shape)輸出
torch.Size([1, 96, 27, 27])至此,一個基本的卷積單元的定義就完成了,包括卷積,啟用,池化.類似的,我們可以寫出後續各層的定義.
AlexNet有5個卷積層,第一個卷積層的卷積核大小為11x11,第二個卷積層的卷積核大小為5x5,其餘的卷積核均為3x3.第一二五個卷積層後做了最大池化操作,視窗大小為3x3,步幅為2.
這樣,卷積層的部分如下:
net = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4,padding=2), #[1,96,55,55] order:batch,channel,h,w
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2), #[1,96,27,27]
nn.Conv2d(96, 256, kernel_size=5, stride=1,padding=2),#[1,256,27,27]
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2), #[1,256,13,13]
nn.Conv2d(256, 384, kernel_size=3, stride=1,padding=1), #[1,384,13,13]
nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, stride=1,padding=1), #[1,384,13,13]
nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, stride=1,padding=1), #[1,256,13,13]
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2), #[1,256,6,6]
)接下來是全連線層的部分:
net = nn.Sequential(
nn.Linear(256*6*6,4096),
nn.ReLU(),
nn.Dropout(0.5), #dropout防止過擬合
nn.Linear(4096,4096),
nn.ReLU(),
nn.Dropout(0.5), #dropout防止過擬合
nn.Linear(4096,10) #我們最終要10分類
)全連線層的引數數量過多,為了防止過擬合,我們在啟用層後面加入了dropout層.
這樣的話我們就可以給出模型定義:
class AlexNet(nn.Module):
def __init__(self):
super(AlexNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=2), # [1,96,55,55] order:batch,channel,h,w
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2), # [1,96,27,27]
nn.Conv2d(96, 256, kernel_size=5, stride=1,padding=2), # [1,256,27,27]
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2), # [1,256,13,13]
nn.Conv2d(256, 384, kernel_size=3, stride=1,padding=1), # [1,384,13,13]
nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, stride=1,padding=1), # [1,384,13,13]
nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, stride=1,padding=1), # [1,256,13,13]
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2), # [1,256,6,6]
)
self.fc = nn.Sequential(
nn.Linear(256*6*6, 4096),
nn.ReLU(),
nn.Dropout(0.5), # dropout防止過擬合
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Dropout(0.5), # dropout防止過擬合
nn.Linear(4096, 10) # 我們最終要10分類
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))#輸入全連線層之前,將特徵展平
return output
載入資料
batch_size,num_workers=32,4
train_iter,test_iter = learntorch_utils.load_data(batch_size,num_workers,resize=224)其中load_data定義於learntorch_utils.py.
def load_data(batch_size,num_workers,resize):
trans = []
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
train=True, download=True,
transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root='/home/sc/disk/keepgoing/learn_pytorch/Datasets/FashionMNIST',
train=False, download=True,
transform=transform)
train_iter = torch.utils.data.DataLoader(
mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(
mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
return train_iter,test_iter這裡,構造了一個transform.對影象做一次resize.
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)定義模型
net = AlexNet().cuda()由於全連線層的存在,AlexNet的引數還是非常多的.所以我們使用GPU做運算
定義損失函式
loss = nn.CrossEntropyLoss()定義優化器
opt = torch.optim.Adam(net.parameters(),lr=0.01)定義評估函式
def test():
acc_sum = 0
batch = 0
for X,y in test_iter:
X,y = X.cuda(),y.cuda()
y_hat = net(X)
acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item()
batch += 1
print('acc_sum %d,batch %d' % (acc_sum,batch))
return 1.0*acc_sum/(batch*batch_size)驗證在測試集上的準確率.
訓練
num_epochs = 3
def train():
for epoch in range(num_epochs):
train_l_sum,batch = 0,0
start = time.time()
for X,y in train_iter:
X,y = X.cuda(),y.cuda()
y_hat = net(X)
l = loss(y_hat,y)
opt.zero_grad()
l.backward()
opt.step()
train_l_sum += l.item()
batch += 1
test_acc = test()
end = time.time()
time_per_epoch = end - start
print('epoch %d,train_loss %f,test_acc %f,time %f' %
(epoch + 1,train_l_sum/(batch*batch_size),test_acc,time_per_epoch))
train()輸出
acc_sum 6297,batch 313
epoch 1,train_loss 54.029241,test_acc 0.628694,time 238.983008
acc_sum 980,batch 313
epoch 2,train_loss 0.106785,test_acc 0.097843,time 239.722055
acc_sum 1000,batch 313
epoch 3,train_loss 0.071997,test_acc 0.099840,time 239.459902明顯出現了過擬合.我們把學習率調整為0.001後,把batch_size調整為128
opt = torch.optim.Adam(net.parameters(),lr=0.001)再訓練,輸出
acc_sum 8714,batch 79
epoch 1,train_loss 0.004351,test_acc 0.861748,time 156.573509
acc_sum 8813,batch 79
epoch 2,train_loss 0.002473,test_acc 0.871539,time 201.961380
acc_sum 8958,batch 79
epoch 3,train_loss 0.002159,test_acc 0.885878,time 202.349568過擬合消失. 同時可以看到AlexNet由於引數過多,訓練還是挺慢
