通過之前的學習，我們知道多變數的線性迴歸。在這節中，將介紹一些可供選擇的特徵以及如何得到不同的學習演算法。當選擇了合適的特徵後，這些演算法往往是非常有效的。另外還將介紹多項式迴歸。它使得我們能夠使用線性迴歸的方法來擬合非常複雜的函式，甚至是非線性函式。

    下面以預測房價為例。假設有兩個特徵，分別是房子臨街寬度和房子深度（實際上相當於長？）。下面是我們想要賣出的房子的圖片。

    然後我們就可以建立一個這樣的線性迴歸模型。其中臨街寬度是我們的第一個特徵x₁，縱深是第二個特徵x₂。但當我們在運用線性迴歸時，我們不一定非要直接用給出x₁

和x₂作為特徵。我們可以自己創造新的特徵。因此，如果我要預測房子的價格，我會做的也許是確認真正能夠決定房子大小的我擁有的土地的大小。因此，我可能會創造一個新的特徵，我稱之為x，臨街寬度與縱深的乘積（這就是我擁有的土地的面積）。於是，我將h_θ(x)₌θ₀+θ₁x 這個式子作為假設，這個式子只用一個特徵（我的土地的面積）。有的時候不直接使用給的特徵，反而使用自己創造的新的特徵，可能會得到一個更好的模型。

    與選擇特徵的想法密切相關的一個概念被稱為多項式迴歸。比方說，有一個這樣的住房價格的資料集。

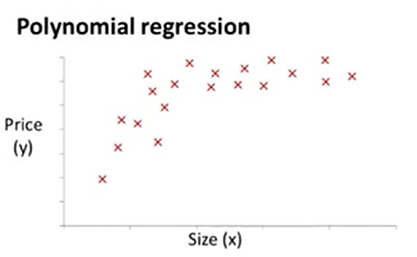
    可能會有多個不同的模型用於擬合.直線似乎並不能很好地擬合這些資料，因此你可能會想到用像下面給出的二次模型去擬合。所以，選擇之一是二次模型。然後，我們可能得到如下的擬合效果。

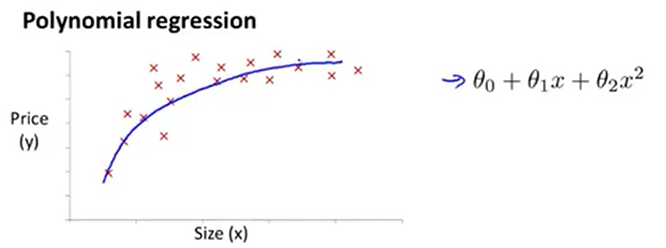
    但是你可能會覺得二次函式模型不合理。因為一個二次函式最終會降下來，但是，我們並不認為，隨著土地面積的增加，價格會下降。因此，我們可能會選擇一個不同的多項式模型並轉而選擇使用一個三次函式。現在我們有了一個三次函式，我們用它進行擬合。也許我們會得到如下的擬合效果。也許這條綠色的線對這個資料集擬合得更好，因為它不會在最後下降。

    使用多元線性迴歸的方法，我們可以對演算法做一個簡單的修改來實現它。按照我們之前假設的形式，我們知道如何去擬合。就像之前的例子，我們知道h_θ(x)=θ₀+θ₁x₁+θ₂x₂+θ₃x₃。而現在，如果我們想擬合這個三次函式模型，我們討論的就是h_θ

(x)=θ₀ + θ₁(size) + θ₂(size)² + θ₃(size)³_。（size表示房子的面積）觀察兩個式子，我們自然就會想到假設x₁=size，x₂=(size)²，x₃=(size)³。然後再應用線性迴歸的方法。我們就可以將一個三次函式擬合到資料上面。這裡還要再說一件事情：如果像這樣選擇特徵，那麼特徵縮放就變得更重要了。如果房子的面積取值範圍在1-1000，那麼房子面積的平方，取值範圍就在1-1000000。而第三個特徵，房子面積的立方取值範圍就在1-100000000。因此，這三個特徵的範圍有很大的不同。所以如果使用梯度下降法，特徵縮放非常重要。這樣才能將值的範圍變得具有可比性。

    最後一個例子將告訴我們其實有很大的餘地來選擇要是有哪些特徵。之前我們談到這樣的二次模型不是最理想的，因為它最後會下降。我們不希望選擇房子面積的增加，價格會下降。但是除了轉而建立一個三次模型以外，我們也許有其他可選的特徵。這裡給出另外一個合理的選擇的例子，他可能是h_θ(x)=θ₀ + θ₁(size) + θ₂(√size)。

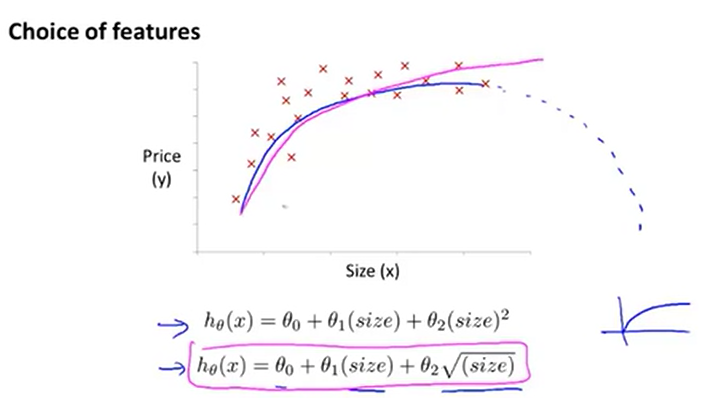
    然後，我們可能得到一條趨勢是上升的，但是慢慢變得平緩的曲線。在這個例子中，憑著對平方根函式影象的瞭解以及對資料形狀的瞭解，通過選擇不同的特徵，有時可以得到更好的模型。

    在這節中，我們探討了多項式迴歸。也就是如何將一個多項式，如一個二次函式或者一個三次函式，擬合到資料上面。我們還討論了我們可以自己選擇使用哪些特徵。

    但是，有很多時候會有很多不同的特徵，而我們該如何決定使用什麼特徵，也許這似乎有點難以抉擇。在後面的課程中，我們將學習一些演算法，它們會自動選擇要使用什麼特徵。因此，可以讓演算法觀察給出的資料，並自動為你選擇到底應該選擇一個二次函式還是一個三次函式還是一個其他的函式。但是在我們學習那種演算法之前，我們要知道我們其實可以自由選擇使用什麼特徵，並且通過設計不同的特徵我們能夠用更復雜的函式擬合數據，而不只是用一條直線去擬合。特別的，你也可以使用多項式函式。有時如果從合適的角度來尋找特徵，你就能得到一個更符合的資料的模型。

&n