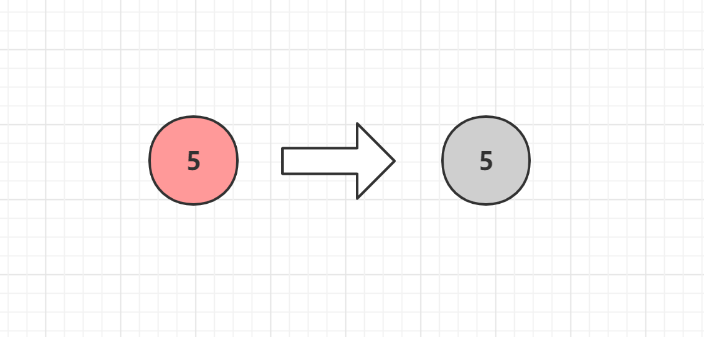
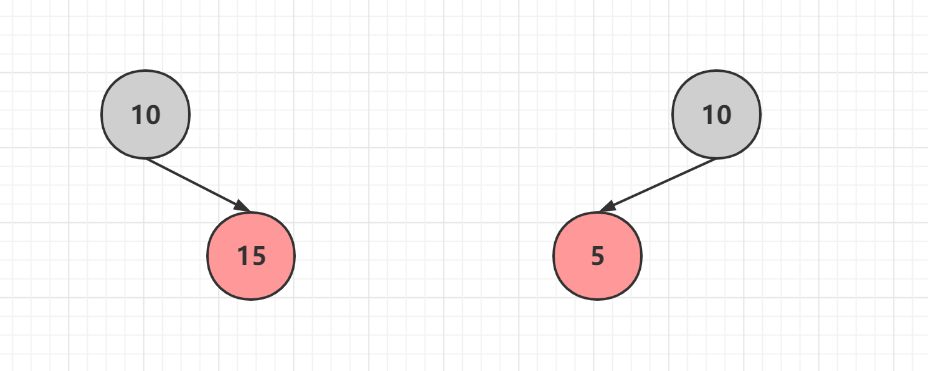
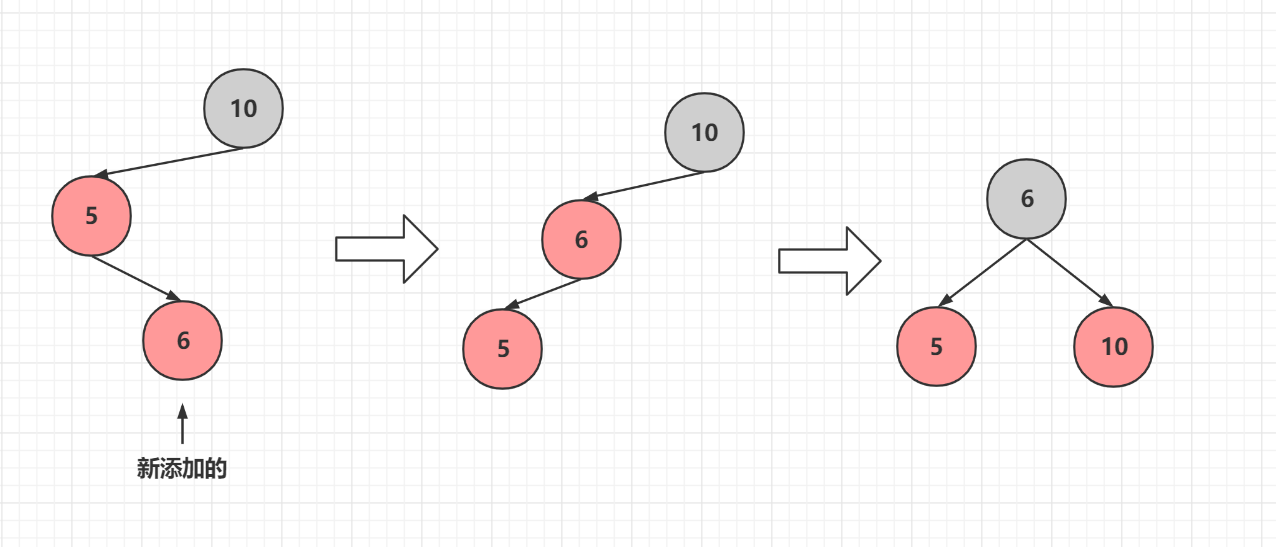
[上一篇寫了234樹對比紅黑樹,和紅黑樹某些情況需要調整的原因,這篇就只寫紅黑樹的新增和刪除](https://www.cnblogs.com/sunankang/p/14309507.html) # 紅黑樹 ## 性質 1. 每個節點要麼紅色要麼黑色 2. 根節點是黑色 3. 每個葉節點是黑色的,這裡葉子節點指空的節點,和二叉樹的葉子節點不同 4. 每個紅色節點的兩個子節點都是黑色 5. 每個節點到它的每個葉子節點的所有路徑都包含相同數目的黑色節點 # 新增 所有新增的節點預設都是紅色 1. 空節點 2. 父節點為黑色 3. 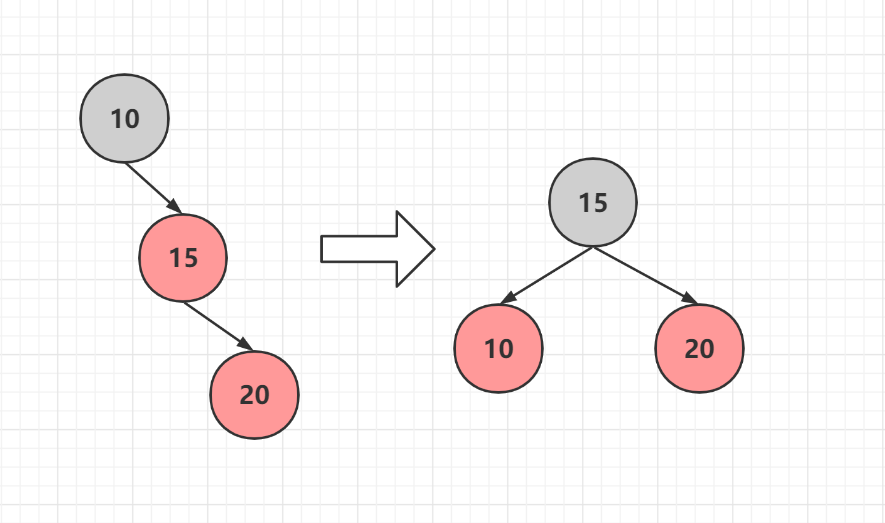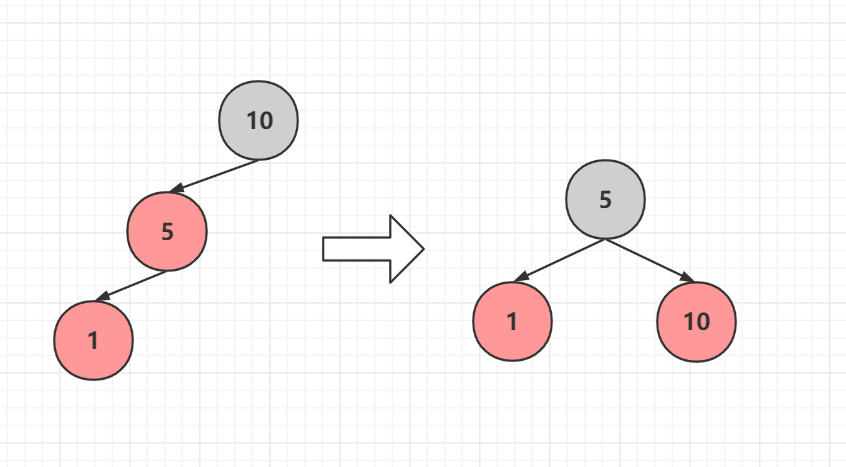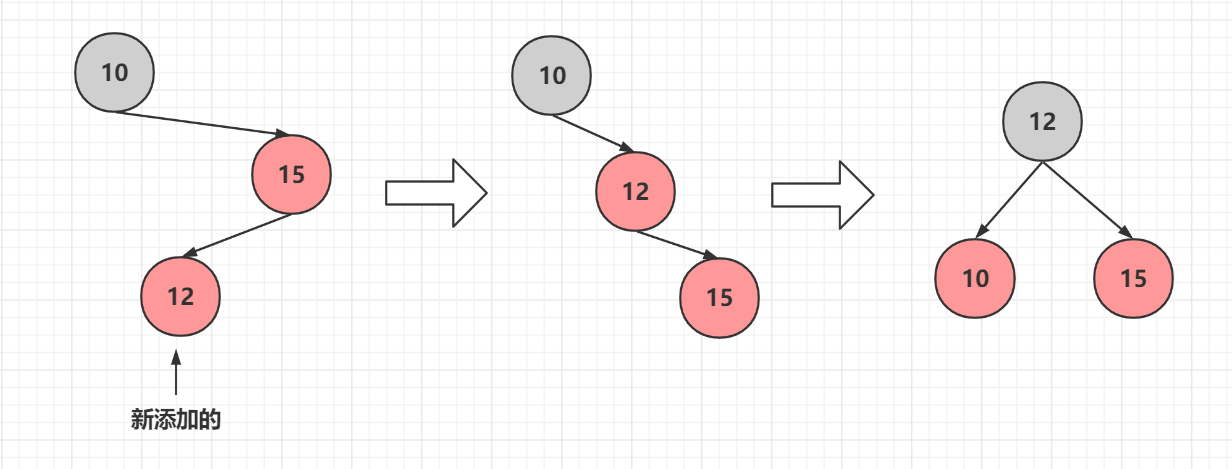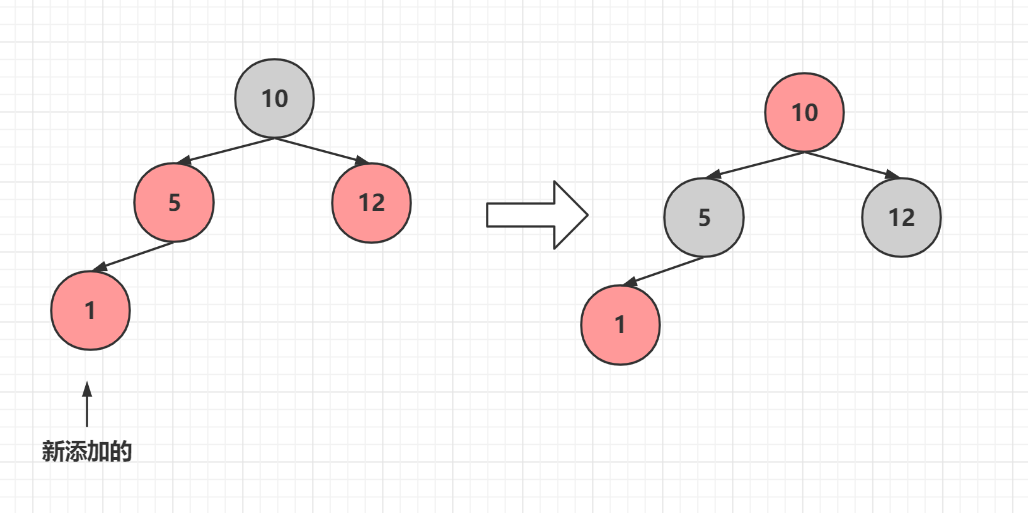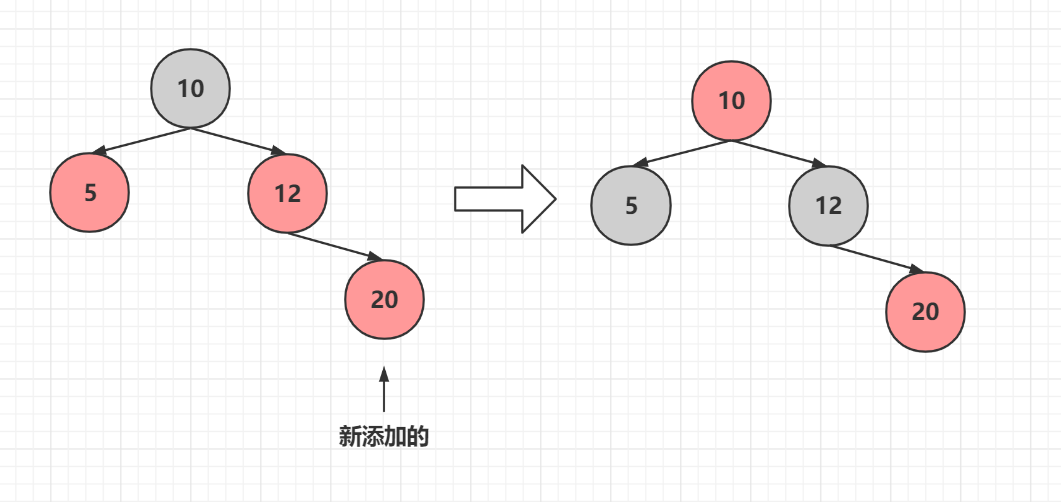父節點為紅色 ## 1 空節點  所有節點預設為紅色,新增後5為根節點,違反了性質2"根節點是黑色" ,只需要將紅變黑即可 ## 2 父節點為黑色 ### 2.1 父節點為黑色,直接新增,小於父新增左邊,大於等於新增右邊  ## 3 父節點為紅色 ### 情況1 祖孫三代在一條線 直接進行旋轉變色即可   而這裡面還有一種情況 我們需要先將5和6進行旋轉,讓它變成上面的情況,然後按照上面的操作進行新增   ### 情況2有叔叔節點 #### 情況2.1叔叔節點為紅色 **如果10節點為跟節點,那麼再變黑**,如果10節點變紅與上面發生衝突,那麼把10節點作為新新增的節點,再繼續執行調整   # 刪除 情況 1. 沒有子節點 2. 有一個子節點 3. 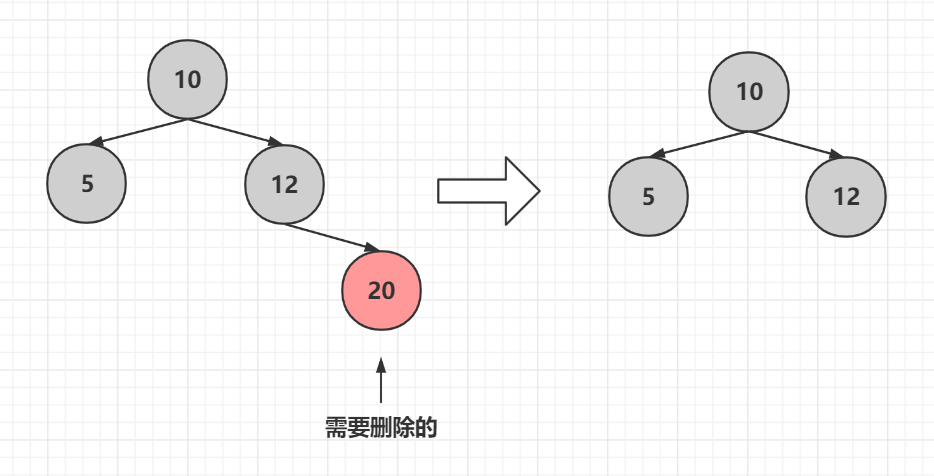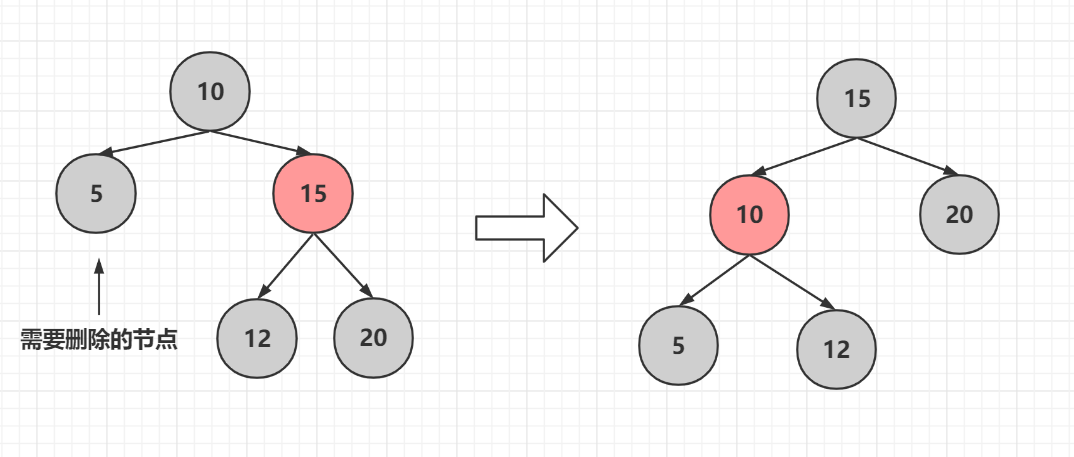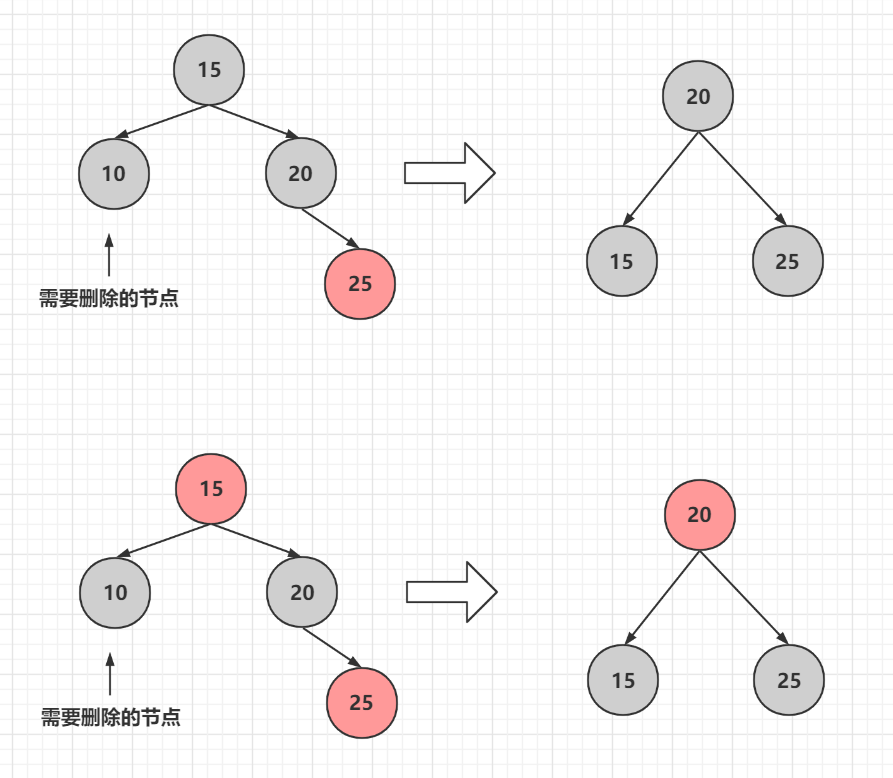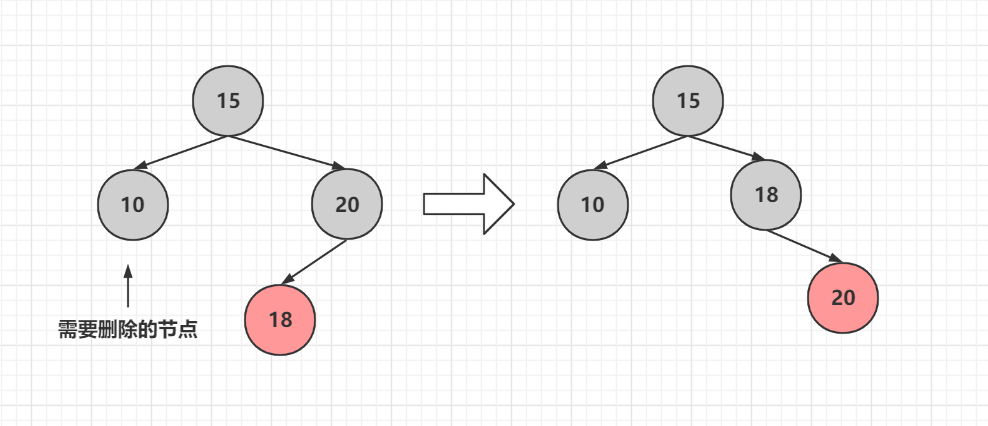有兩個子節點 先說有兩個子節點的情況,需要尋找到它的前驅或後繼節點來替代,然後刪除前驅或後繼節點,也就是將情況轉換為1或2 關於前驅或後繼節點看上篇文章 ## 沒有子節點 ### 1.1 節點為紅色 沒有子節點且當前節點為紅色直接刪除  ### 1.2 節點為黑色 1.2.1兄弟節點為紅色 1.2.2兄弟節點為黑色且有一個子節點 1.2.3兄弟節點為黑色且有兩個子節點 1.2.4兄弟節點為黑色,沒有子節點 ### 1.2.1兄弟節點為紅色 需要將兄弟節點進行旋轉變色,為什麼兄弟節點為紅色需要旋轉變色原因可以看上一篇部落格,將情況變為234   ### 1.2.2兄弟節點為黑色且有一個子節點  在這裡面還有一種 小情況,兄弟節點的子節點如果離自己近需要先進行旋轉變色,將情況變成上面的再進行操作  ### 1.2.3兄弟節點為黑色且有兩個子節點 有兩種解決方法 1 先刪除5同時將15和20進行右旋變色,然後10和15進行左旋變色,而20和15就是上面的情況,**旋轉完後15兩個子節點必須是黑色**,如果15節點於紅黑樹性質衝突,那麼在根據情況調整  2 直接刪除5,然後10和20進行左旋,一般都用這個方法,減少一次旋轉  ### 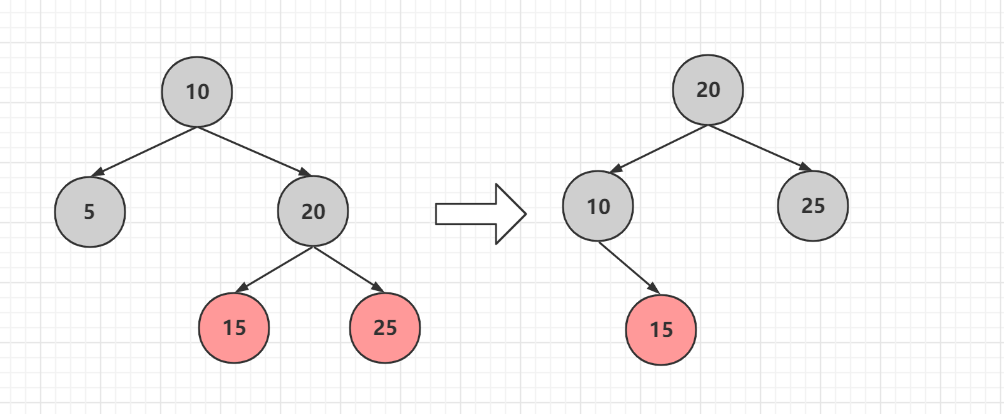1.2.4兄弟節點為黑色,沒有子節點 父節點為紅色 刪除5,然後兄弟節點變為紅色來維持父節點的左右黑色平衡,如果父節點為紅色,直接變黑即可,父節點變黑是維護爺爺節點的左右黑色平衡  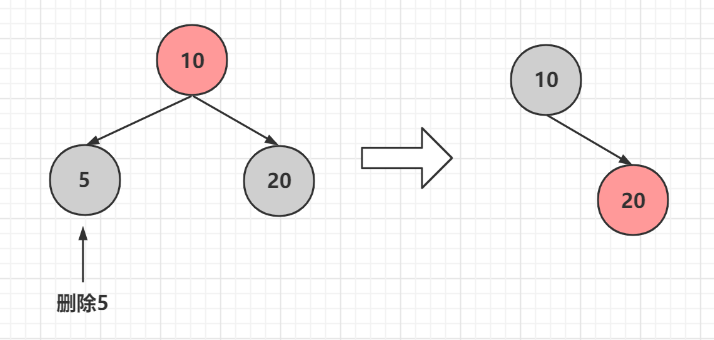如果父節點為黑色 同樣也是將兄弟節點變紅,然後把父節點向上遞迴處理 刪除一個黑色節點,然後改一個紅色節點,這個父節點的黑色是平衡了,如果上面還有節點呢,那麼黑色節點還是不平衡, 這時就需要遞迴進行操作,直到出現紅色父節點將其變為黑色或到達根節點為止 ## 有子節點 1. 刪除節點為紅色 2. 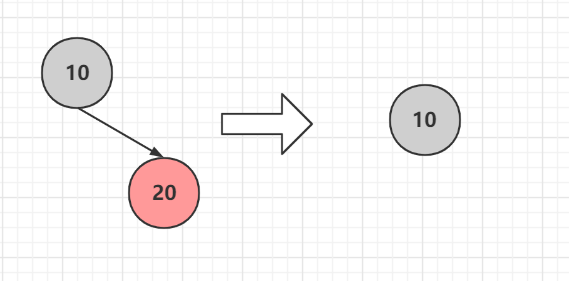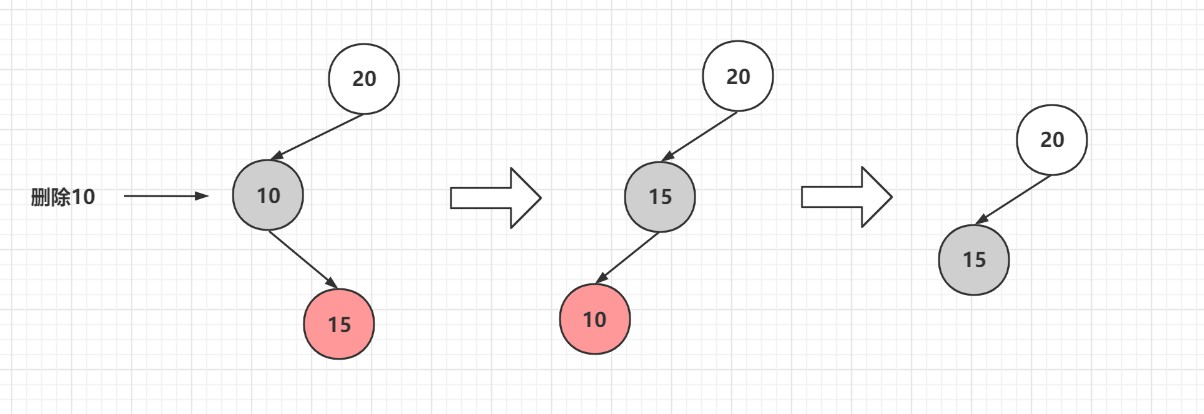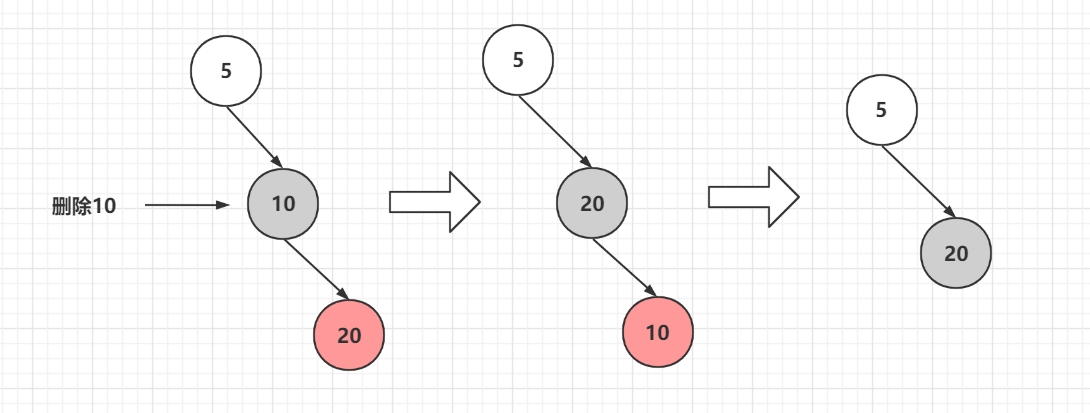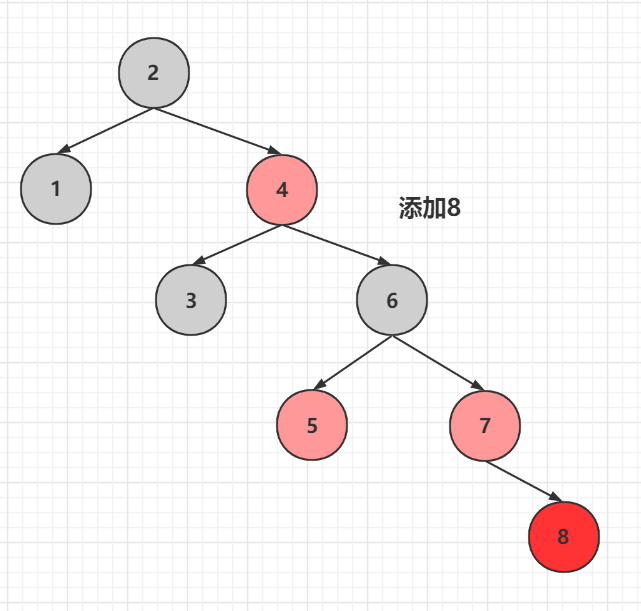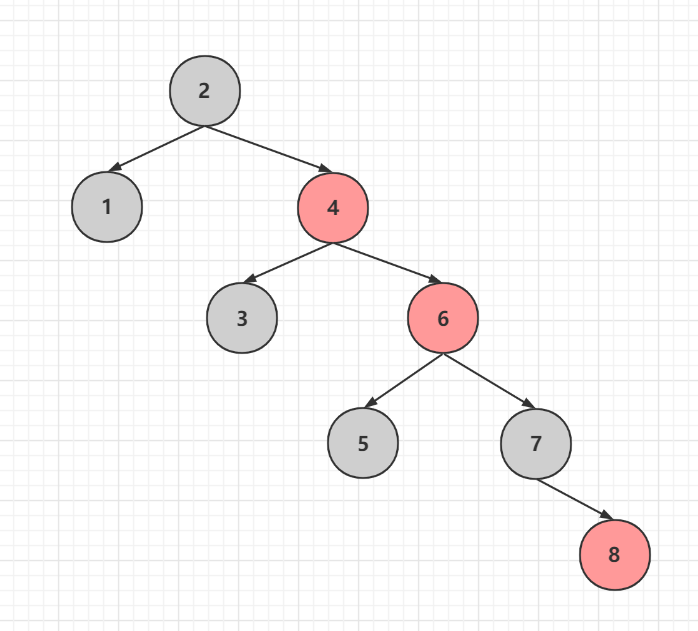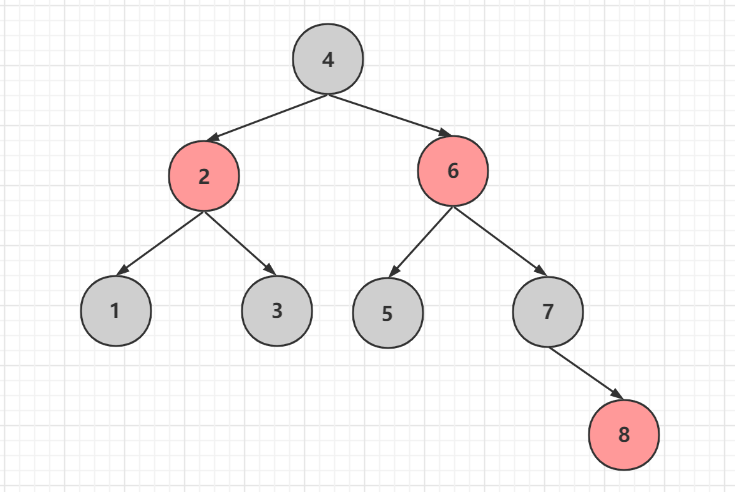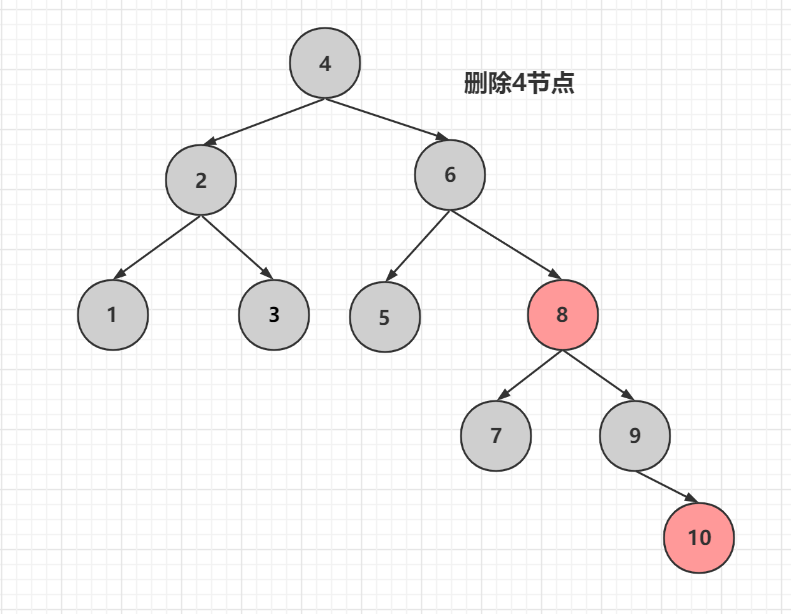刪除節點為黑色 ### 1 刪除節點為紅色 直接刪除  ### 2 刪除節點為黑色 只會有一種情況,有一個紅色的左孩子或右孩子,如果有兩個孩子那麼就會去刪除前驅或後置而不是當前節點, 也不可能出現一個孩子為黑色一個孩子為紅色,更不可能出現只有一個黑色孩子,根據紅黑樹性質5就明白了 那麼來看只有一個紅色子節點情況 先將10和它的紅色子節點20進行旋轉變色,然後直接刪除,5節點可以是紅也可以是黑   ## 練習 ### 新增  屬於有父節點和叔叔節點,且都為紅色,根據新增的3.2.1父節點和叔叔節點都為紅色進行變色處理  完成後發現因為變色6節點和4節點出現了連續兩個紅色,需要繼續調整,把6當做新新增的節點,發現屬於情況3.1祖孫三代在一條線,將2和4節點進行旋轉變色  ### 刪除 我們刪除4節點,這裡4就是根節點  首先判斷是那種情況,有兩個子節點那就是尋找前驅或後繼進行替換,我們這裡使用前驅節點,也就是3  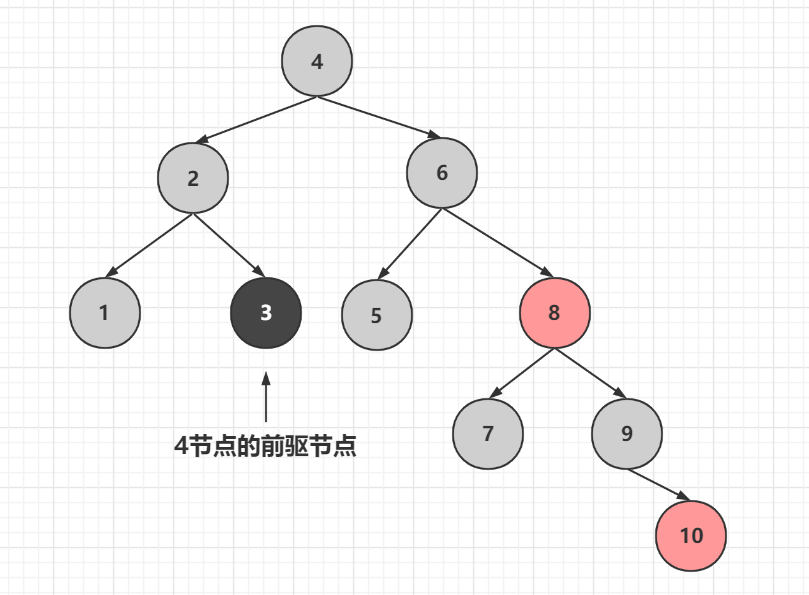首先判斷3節點的情況,沒有子節點,兄弟節點也沒有節點,那就是刪除情況的1.2.4兄弟節點為黑色,沒有子節點 首先將值覆蓋掉,然後刪除3節點,將3節點的兄弟節點變色為紅色  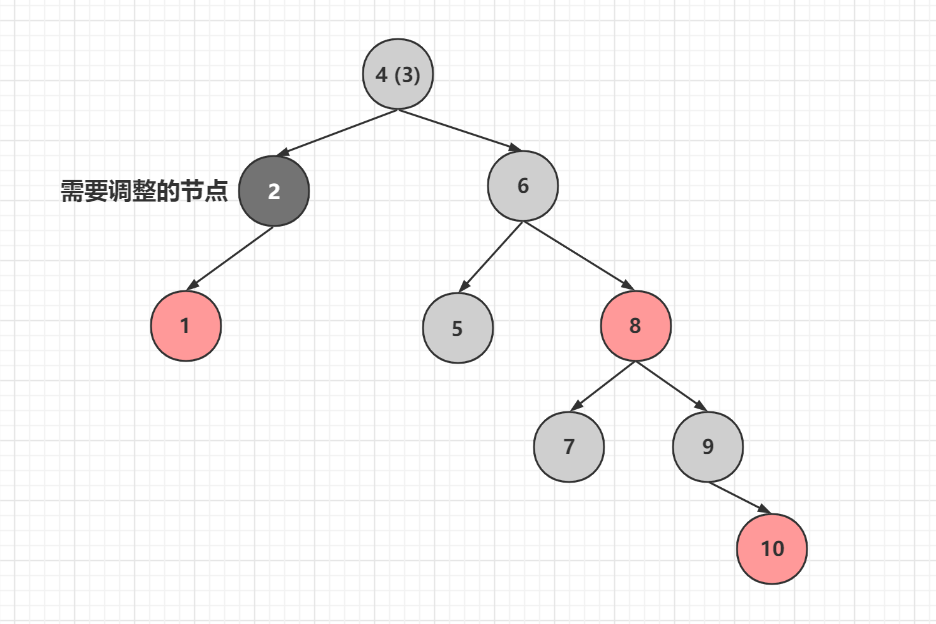然後發現父節點為黑色,不能進行變色來平衡,那麼把2節點當做需要刪除的節點(並不真正刪除)繼續調整 發現兄弟節點為黑色且有兩個子節點,屬於刪除情況的1.2.3,只需要進行旋轉即可  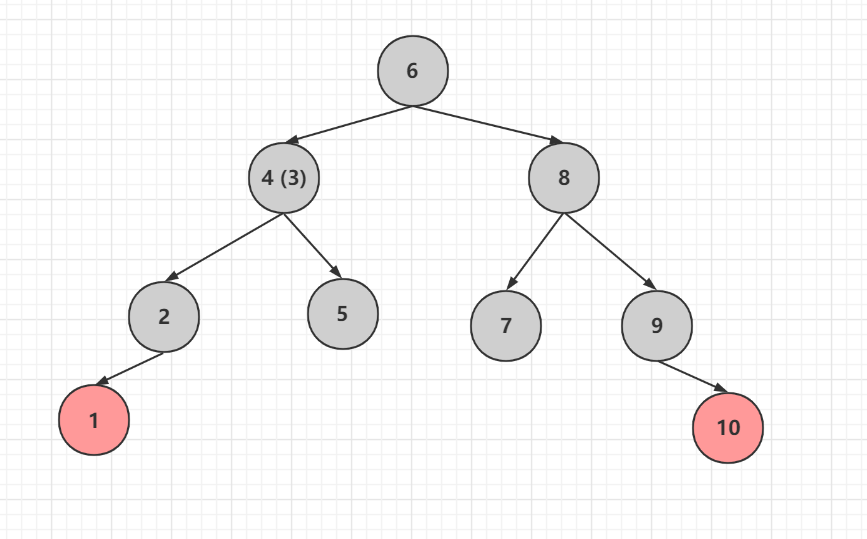刪除節點6  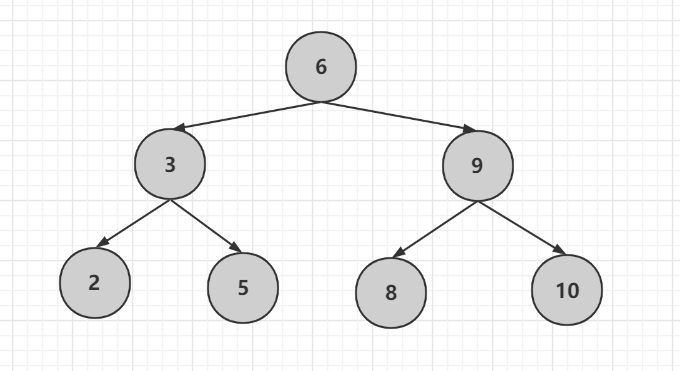有兩個節點,尋找前驅或後繼,這次我們使用後繼節點,也就是8,還是首先把值賦給6,然後進行刪除  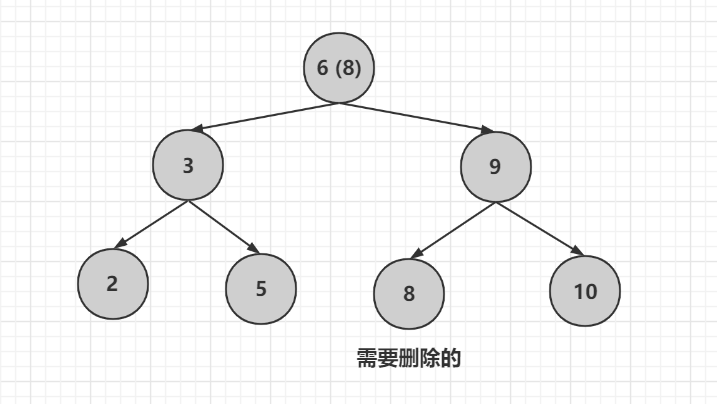將8刪除,兄弟節點變色,發現父節點為黑色,不能進行變色保持黑色平衡,那麼只能向上遞迴  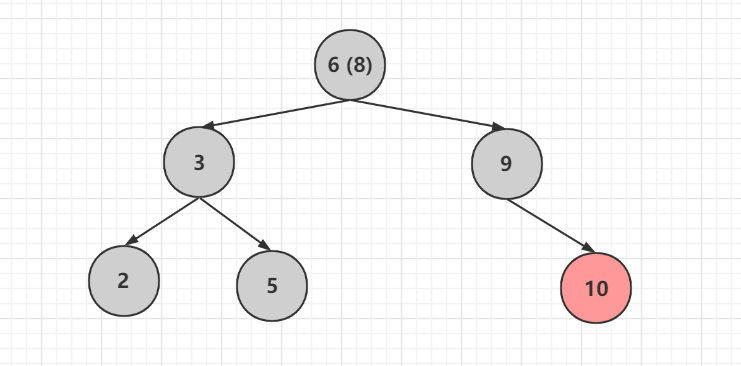將9的兄弟節點變色為紅色,如果這個6 (8)節點 如果還有父親則繼續遞迴操作,現在發現到根節點,調整完成  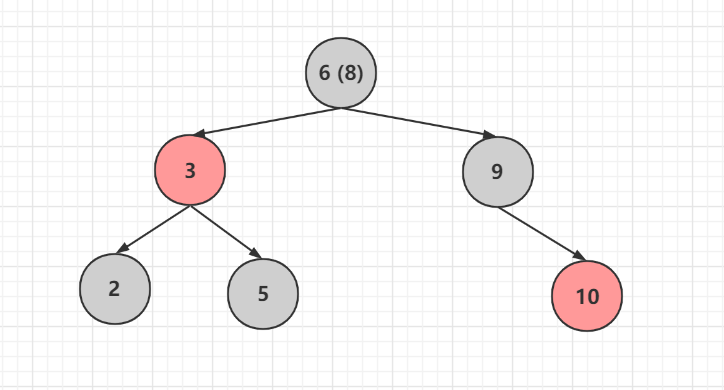本文僅個人理解,如果有不對的地方歡迎評論指出或私信,謝謝٩(๑>