洛谷P3414 SAC#1 - 組合數
阿新 • • 發佈:2017-11-07
radius blank span 輸出 range .com 輸入輸出格式 描述 www. 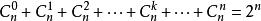 2、
2、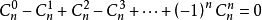 3、
3、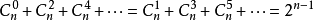
洛谷P3414 SAC#1 - 組合數
題目描述
辣雞蒟蒻SOL是一個傻逼,他居然覺得數很萌!
今天他萌上了組合數。現在他很想知道simga(C(n,i))是多少;其中C是組合數(即C(n,i)表示n個物品無順序選取i個的方案數),i取從0到n所有偶數。
由於答案可能很大,請輸出答案對6662333的余數。
輸入輸出格式
輸入格式:
輸入僅包含一個整數n。
輸出格式:
輸出一個整數,即為答案。
輸入輸出樣例
輸入樣例#1: 復制3輸出樣例#1: 復制
4
說明
對於20%的數據,n <= 20;
對於50%的數據,n <= 1000;
對於100%的數據,n <= 1 000 000 000 000 000 000 (10^18)
分析
原文地址
1、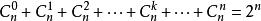 2、
2、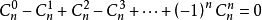 3、
3、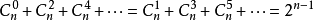
證明:由當$a = b = 1$時,代入二項式定理可證明$1$式; 當$a = -1$,$b = 1$時代入二項式定理可證明$2$式;代入$a = 1$,$b = -1$可得到另一個意義相同的式子; $(1式+2式) \over 2$可證明$3$式。
代碼
又復習了一下二項式定理。
#include<cstdio> using namespace std; const long long mo=6662333; long long ksm(long long a,long long p){ if(p<0) return 0; long long res=1; a%=mo; //這兒要先對a取模 for(;p;p>>=1,a=a*a%mo) if(p&1) res=res*a%mo; return res; } int main(){ long long n; scanf("%lld",&n); printf("%lld",ksm(2,n-1)); return 0; }
洛谷P3414 SAC#1 - 組合數
