P2458 [SDOI2006]保安站崗

題意

題目描述

五一來臨，某地下超市為了便於疏通和指揮密集的人員和車輛，以免造成超市內的混亂和擁擠，準備臨時從外單位呼叫部分保安來維持交通秩序。

已知整個地下超市的所有通道呈一棵樹的形狀；某些通道之間可以互相望見。總經理要求所有通道的每個端點（樹的頂點）都要有人全天候看守，在不同的通道端點安排保安所需的費用不同。

一個保安一旦站在某個通道的其中一個端點，那麼他除了能看守住他所站的那個端點，也能看到這個通道的另一個端點，所以一個保安可能同時能看守住多個端點（樹的結點），因此沒有必要在每個通道的端點都安排保安。

程式設計任務：

請你幫助超市經理策劃安排，在能看守全部通道端點的前提下，使得花費的經費最少。

輸入輸出格式

輸入格式：

第\(1\)行\(n\)，表示樹中結點的數目。

第\(2\)行至第\(n+1\)行，每行描述每個通道端點的資訊，依次為：該結點標號\(i(0<i\leq n)\)，在該結點安置保安所需的經費\(k(k\leq 10000)\)，該邊的兒子數\(m\)，接下來\(m\)個數，分別是這個節點的\(m\)個兒子的標號\(r_1,r_2,\dots ,r_m\)。

對於一個\(n(0<n\leq 1500)\)個結點的樹，結點標號在\(1\)到\(n\)之間，且標號不重複。

輸出格式：

最少的經費。

如右圖的輸入資料示例

輸出資料示例：

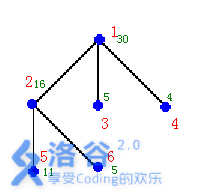
輸入輸出樣例

輸入樣例#1：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

輸出樣例#1：

25

說明

樣例說明：在結點\(2,3,4\)安置\(3\)個保安能看守所有的\(6\)個結點，需要的經費最小：\(25\)

思路

開始復健樹形\(dp\)。

對於每一個結點，可能有三種保護狀態：被兒子保護，被自己保護，被父親保護。所以我們可以這樣設計狀態：\(f[i][0/1/2]\)表示結點\(i\)的三種狀態下的子樹最小經費要求。在下面的程式碼中，\(0\)表示被父親保護，\(1\)表示被兒子保護，\(2\)表示被自己保護。轉移方程也很簡單了。

void dfs(int now)
{
    dp[now][0]=0,dp[now][1]=0x3f3f3f3f,dp[now][2]=val[now];//初始值
    for(int i=top[now];i;i=nex[i])
    {
        dfs(to[i]);
        dp[now][0]+=min(dp[to[i]][1],dp[to[i]][2]);//兒子不可能被自己保護
        dp[now][2]+=min(dp[to[i]][0],min(dp[to[i]][1],dp[to[i]][2]));//兒子的保護狀態可以隨意選擇。
    }
    for(int i=top[now];i;i=nex[i]) dp[now][1]=min(dp[now][1],dp[now][0]-min(dp[to[i]][1],dp[to[i]][2])+dp[to[i]][2]);//相當於直接記錄最大花費的兒子
}
 

AC程式碼

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1505;
int n,val[MAXN],dp[MAXN][3];
int cnt,top[MAXN],to[MAXN],nex[MAXN];
bool vis[MAXN];
int read()
{
    int re=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void dfs(int now)
{
    dp[now][0]=0,dp[now][1]=0x3f3f3f3f,dp[now][2]=val[now];
    for(int i=top[now];i;i=nex[i])
    {
        dfs(to[i]);
        dp[now][0]+=min(dp[to[i]][1],dp[to[i]][2]);
        dp[now][2]+=min(dp[to[i]][0],min(dp[to[i]][1],dp[to[i]][2]));
    }
    for(int i=top[now];i;i=nex[i]) dp[now][1]=min(dp[now][1],dp[now][0]-min(dp[to[i]][1],dp[to[i]][2])+dp[to[i]][2]);
}
int main()
{
    n=read();
    for(int i=0;i<n;i++)
    {
        int x=read();val[x]=read();int j=read();
        while(j--)
        {
            int y=read();vis[y]=true;
            to[++cnt]=y,nex[cnt]=top[x],top[x]=cnt;
        }
    }
    for(int i=1;i<=n;i++)
        if(!vis[i])
        {
            dfs(i);
            printf("%d",min(dp[i][1],dp[i][2]));
            return 0;
        }
}