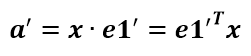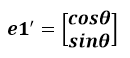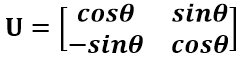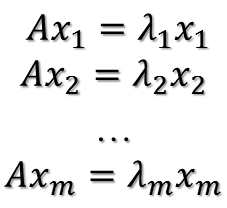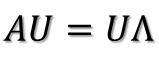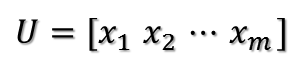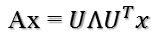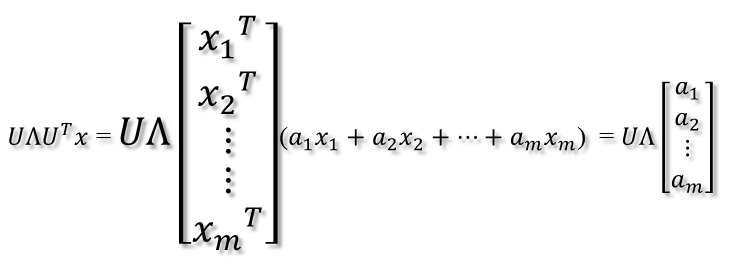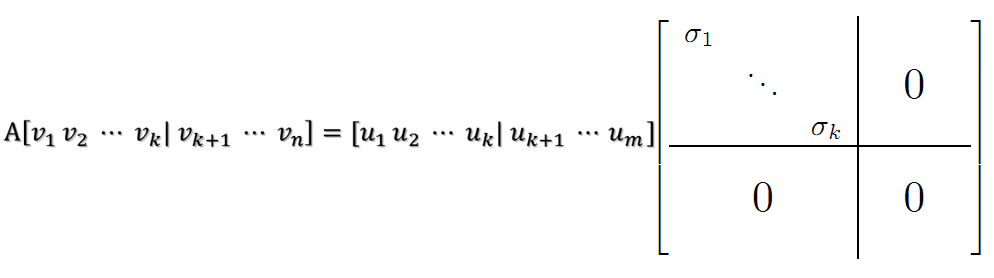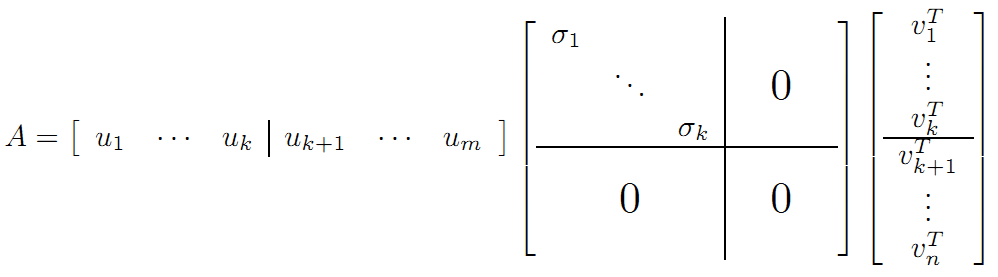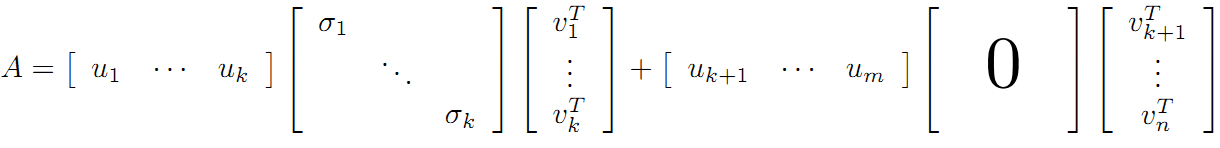低秩分解
十歲的小男孩
目錄
概念
1. 奇異值（SVD）分解
2. 張量分解
2.1 CP 分解( Canonical Polyadic Decomposition (CPD)
2.2 TD 分解( Tucker Decomposition )
2.3 BTD 分解（block term decomposition）
概念
本章節涉及到線性代數的知識，磨刀不誤砍柴工，理解基本的概念知識是有必要的。該章節的初衷為模型壓縮的一個小節，當然在其他領域比如PCA，推薦等都有應用。首先應清楚學習本章的意義，該知識點能夠解決什麼問題，其後在深入該如何用。後序對低秩的三個子方法淺顯的講解。
1. 秩（Rank）
為了從方程組中去掉多餘的方程，引出了“矩陣的秩”。矩陣的秩度量的就是矩陣的行列之間的相關性。為了求矩陣A的秩，我們是通過矩陣初等變換把A化為階梯型矩陣，若該階梯型矩陣有r個非零行，那A的秩rank(A)就等於r。 如果矩陣的各行或列是線性無關的，矩陣就是滿秩的，也就是秩等於行數。
2. 低秩（Low-Rank）
如果X是一個m行n列的數值矩陣，rank(X)是X的秩，假如rank (X)遠小於m和n，則我們稱X是低秩矩陣。低秩矩陣每行或每列都可以用其他的行或列線性表出，可見它包含大量的冗餘資訊。利用這種冗餘資訊，可以對缺失資料進行恢復，也可以對資料進行特徵提取。
3. 低秩分解（Low Rank Filters）
目的：去除冗餘，並且減少權值引數
方法：採用兩個K*1的卷積核替換掉一個K*K的卷積核(decompose the K convolutions into two separable convolutions of size 1 × K and K × 1)
原理：權值向量主要分佈在一些低秩子空間，用少數基來重構權值矩陣
參考： (ICCV 2017) Coordinating Filters for Faster Deep Neural Networks
4. 矩陣補全（Matrix Completion）
目的：是為了估計矩陣中缺失的部分（不可觀察的部分），可以看做是用矩陣X近似矩陣M，然後用X中的元素作為矩陣M中不可觀察部分的元素的估計。
5. 矩陣分解（Matrix Factorization）
目的：是指用 A*B 來近似矩陣M，那麼 A*B 的元素就可以用於估計M中對應不可見位置的元素值，而A*B可以看做是M的分解，所以稱作Matrix Factorization。
這是因為協同過濾本質上是考慮大量使用者的偏好資訊（協同），來對某一使用者的偏好做出預測（過濾），那麼當我們把這樣的偏好用評分矩陣M表達後，這即等價於用M其他行的已知值（每一行包含一個使用者對所有商品的已知評分），來估計並填充某一行的缺失值。若要對所有使用者進行預測，便是填充整個矩陣，這是所謂“協同過濾本質是矩陣填充”。
那麼，這裡的矩陣填充如何來做呢？矩陣分解是一種主流方法。這是因為，協同過濾有一個隱含的重要假設，可簡單表述為：如果使用者A和使用者B同時偏好商品X，那麼使用者A和使用者B對其他商品的偏好性有更大的機率相似。這個假設反映在矩陣M上即是矩陣的低秩。極端情況之一是若所有使用者對不同商品的偏好保持一致，那麼填充完的M每行應兩兩相等，即秩為1。
所以這時我們可以對矩陣M進行低秩矩陣分解，用U*V來逼近M，以用於填充——對於使用者數為m，商品數為n的情況，M是m*n的矩陣，U是m*r，V是r*n，其中r是人工指定的引數。這裡利用M的低秩性，以秩為r的矩陣M’=U*V來近似M，用M’上的元素值來填充M上的缺失值，達到預測效果。
低秩分解主要分為以下三個（SVD分解、Tucker分解、Block Term分解）
1. 奇異值（SVD）分解
論文：A Singularly Valuable Decomposition The SVD of a Matrix
特徵值分解和奇異值分解在機器學習領域的方法，讓機器學會抽取重要的特徵。 可以將一個比較複雜的矩陣用更小更簡單的幾個子矩陣的相乘來表示，這些小矩陣描述的是矩陣的重要的特性。兩者關係緊密，特徵值分解和奇異值分解的目的都是一樣，就是提取出一個矩陣最重要的特徵。區別在於，特徵值分解針對方陣而言，奇異值分解可以針對任意矩陣進行分解。循序漸進的首先搞清楚其特徵值分解，再理解奇異值分解。這個章節內容建議看看吳軍的《數學之美》第十五章節，通過例子講解了在文字處理中的兩個分類問題，通俗易懂。
A. 特徵值分解
1. 特徵值
如果說一個向量v是方陣A的特徵向量，將一定可以表示成下面的形式： 
，這時候λ就被稱為特徵向量v對應的特徵值，一個矩陣的一組特徵向量是一組正交向量。特徵值分解是將一個矩陣分解成下面的形式：
，其中Q是這個矩陣A的特徵向量組成的矩陣，Σ是一個對角陣，每一個對角線上的元素就是一個特徵值。這裡引用了一些參考文獻中的內容來說明一下。首先，要明確的是，一個矩陣其實就是一個線性變換，因為一個矩陣乘以一個向量後得到的向量，其實就相當於將這個向量進行了線性變換。比如說下面的一個矩陣： 
，它其實對應的線性變換是下面的形式：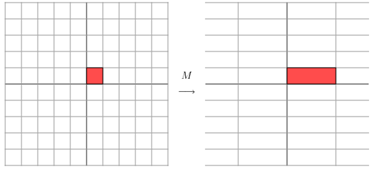
因為這個矩陣M乘以一個向量(x,y)的結果是：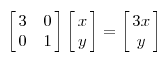
，該矩陣是對稱的，所以這個變換是一個對x，y軸的方向一個拉伸變換（每一個對角線上的元素將會對一個維度進行拉伸變換，當值>1時，是拉長，當值<1時時縮短），當矩陣不是對稱的時候，假如說矩陣是下面的樣子：
它所描述的變換是下面的樣子：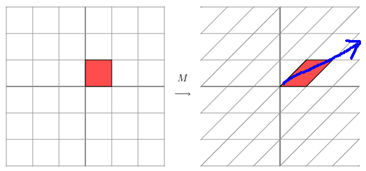
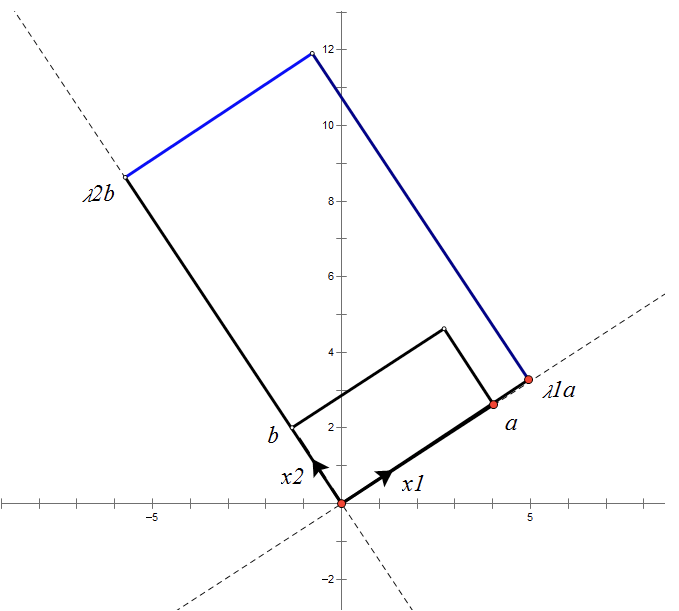
這其實是在平面上對一個軸進行的拉伸變換（如藍色的箭頭所示），在圖中，藍色的箭頭是一個最主要的變化方向（變化方向可能有不止一個），如果我們想要描述好一個變換，那我們就描述好這個變換主要的變化方向就好了。反過頭來看看之前特徵值分解的式子，分解得到的Σ矩陣是一個對角陣，裡面的特徵值是由大到小排列的，這些特徵值所對應的特徵向量就是描述這個矩陣變化方向（從主要的變化到次要的變化排列）。
當矩陣是高維的情況下，那麼這個矩陣就是高維空間下的一個線性變換，這個線性變化可能沒法通過圖片來表示，但是可以想象，這個變換也同樣有很多的變換方向，我們通過特徵值分解得到的前N個特徵向量，那麼就對應了這個矩陣最主要的N個變化方向。我們利用這前N個變化方向，就可以近似這個矩陣（變換）。也就是之前說的：提取這個矩陣最重要的特徵。總結一下，特徵值分解可以得到特徵值與特徵向量，特徵值表示的是這個特徵到底有多重要，而特徵向量表示這個特徵是什麼，可以將每一個特徵向量理解為一個線性的子空間，我們可以利用這些線性的子空間幹很多的事情。不過，特徵值分解也有很多的侷限，比如說變換的矩陣必須是方陣。
2. 正交矩陣
正交矩陣是在歐幾里得空間裡的叫法，在酉空間裡叫酉矩陣，一個正交矩陣對應的變換叫正交變換，這個變換的特點是不改變向量的尺寸和向量間的夾角。下圖是一個直觀的認識：
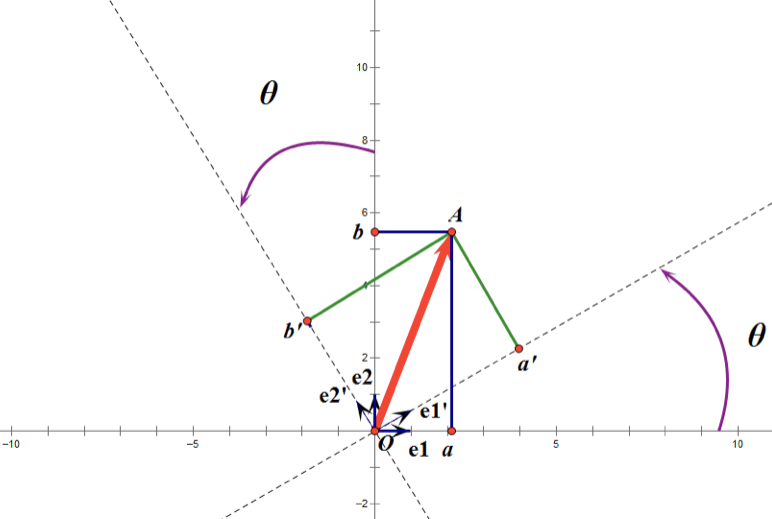
假設二維空間中的向量OA，它在標準座標系（也就是e1和e2表示的座標系）中的表示為(a,b)’(‘表示轉置)；現在用另一組座標e1’、e2’表示為(a’,b’)’;那麼存在矩陣U使得(a’,b’)’=U(a,b)’,而矩陣U就是正交矩陣。
通過上圖可知，正交變換隻是將變換向量用另一組正交基來表示，在這個過程中並沒有罪向量作拉伸，也不改變向量的空間位置，對兩個向量同時做正交變換，變換的前後兩個向量的夾角顯然也不會改變。上圖是一個旋轉的正交變換，可以把e1’、e2’座標系看做是e1、e2座標系經過旋轉某個θ角度得到，具體的旋轉規則如下：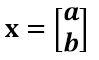 
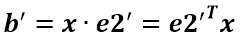
a’和b’實際上是x在e1’和e2’軸上投影的大小，所以直接做內積可得：
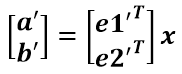
從圖中可以看到：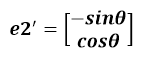 
所以：
正交矩陣U的行(列)之間都是單位正交向量，它對向量做旋轉變換。這裡解釋一下：旋轉是相對的，就那上面的圖來說，我們可以說向量的空間位置沒有變，標準參考系向左旋轉了θ角度，而如果我選擇了e1’、e2’作為新的標準座標系，那麼在新座標系中OA（原標準座標系的表示）就變成了OA’，這樣看來就好像座標系不動，把OA往順時針方向旋轉了θ角度，這個操作實現起來很簡單：將變換後的向量座標仍然表示在當前座標系中。 正交變換的另一個方面是反射變換，也即e1’的方向與圖中方向相反。
總結：正交矩陣的行（列）向量都是兩兩正交的單位向量，正交矩陣對應的變換為正交變換，它有兩種表現：旋轉和反射。正交矩陣將標準正交基對映為標準正交基（即圖中從e1、e2到e1’、e2’）。
3. 特徵值分解（EVD）
在討論SVD之前，先了解矩陣的特徵值分解(EVD)，這裡選擇特殊的矩陣——對角陣，對稱矩陣又一個性質就是總能相似對角化，對稱矩陣不同特徵值對應的特徵向量兩兩正交。一個矩陣能能相似對角化即說明其特徵子空間即為其列空間，若不能對角化則其特徵子空間為列空間的子空間。現在假設存在m * m的滿秩對稱矩陣A，它有m個不同的特徵值，設特徵值為：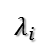
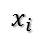
進而：
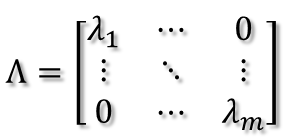
所以可得到A的特徵值分解（由於對稱陣特徵向量兩兩正交，所以U為正交陣，正交陣的逆矩陣等於其轉置）: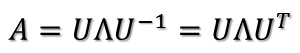 
這裡假設A有m個不同的特徵值，實際上，只要A是對稱陣其均有如上分解。
矩陣A分解了，相應的，其對應的對映也分解為三個對映。現在假設有x向量，用Ａ將其變換到Ａ的列空間中，那麼首先由UT先對x做變換：
U是正交陣UT也是正交陣，所以UT對x的變換是正交變換，它將x用新的座標系來表示，這個座標系就是A的所有正交的特徵向量構成的座標系。比如將x用A的所有特徵向量表示為：
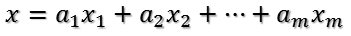
則通過第一個變換就可以把x表示為[a1 a2 … am]T：
緊接著，在新的座標系表示下，由中間那個對角矩陣對新的向量座標換，其結果就是將向量往各個軸方向拉伸或壓縮：
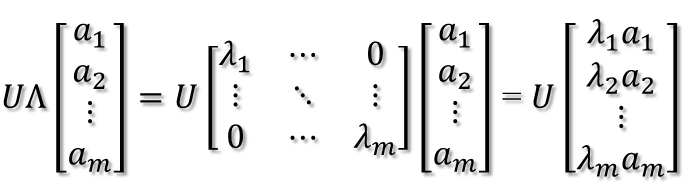
從上圖可以看到，如果A不是滿秩的話，那麼就是說對角陣的對角線上元素存在0，這時候就會導致維度退化，這樣就會使對映後的向量落入m維空間的子空間中。
最後一個變換就是U對拉伸或壓縮後的向量做變換，由於U和UT是互為逆矩陣，所以U變換是UT變換的逆變換。
因此，從對稱陣的分解對應的對映分解來分析一個矩陣的變換特點是非常直觀的。假設對稱陣特徵值全為1那麼顯然它就是單位陣，如果對稱陣的特徵值有個別是0其他全是1，那麼它就是一個正交投影矩陣，它將m維向量投影到它的列空間中。
根據對稱陣A的特徵向量，如果A是2 * 2的，那麼就可以在二維平面中找到這樣一個矩形，是的這個矩形經過A變換後還是矩形：
這個矩形的選擇就是讓其邊都落在A的特徵向量方向上，如果選擇其他矩形的話變換後的圖形就不是矩形了！
B. 奇異值分解
1. 奇異值
特徵值分解是提取矩陣特徵不錯的方法，但侷限在於只針對方陣。奇異值分解可以解決任意矩陣的分解。
假設A是一個M * N的矩陣，那麼得到的U是一個M * M的方陣（裡面的向量是正交的，U裡面的向量稱為左奇異向量），Σ是一個M * N的矩陣（除了對角線的元素都是0，對角線上的元素稱為奇異值），V’(V的轉置)是一個N * N的矩陣，裡面的向量也是正交的，V裡面的向量稱為右奇異向量），從圖片來反映幾個相乘的矩陣的大小可得下面的圖片: 
那麼矩陣A的奇異值和方陣的特徵值是如何對應的?
我們將一個矩陣AT * A，將會得到一個方陣，我們用這個方陣求特徵值可以得到：
這裡得到的Vi就是上面的右奇異向量，此外，我們可以得到：
這裡的σi就是上面說的奇異值。ui就是上面的左奇異向量。奇異值σ跟特徵值相似，在矩陣Σ中也是按從大到小的方式排列，而且σ的值減小的特別的快，在很多的情況下前10%甚至1%的奇異值之和就佔了全部奇異值之和的99%以上。也就是說可以用前r個大的奇異值來近似的描述矩陣，這裡定義奇異值的分解： 
r是一個遠遠小於m和n的值，矩陣的乘法看起來是這個樣子：
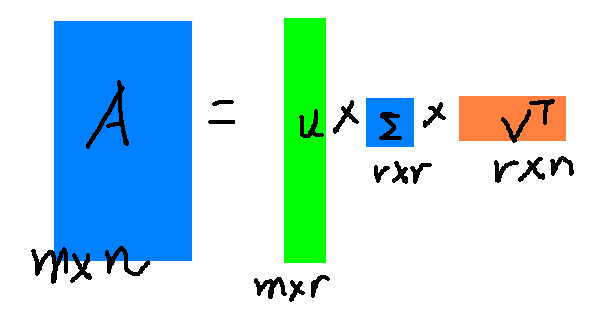
右邊的三個矩陣相乘的結果將會是一個接近於A的矩陣，在這兒，r越接近於n，則相乘的結果越接近於A。而這三個矩陣的面積之和（在儲存觀點來說，矩陣面積越小，儲存量就越小）要遠遠小於原始的矩陣A，我們如果想要壓縮空間來表示原矩陣A，我們存下這裡的三個矩陣：U、Σ、V就好了。
2. 奇異值分解 SVD
上面的特徵值分解的A矩陣是對稱陣，根據EVD可以找到一個（超）矩形使得變換後還是（超）矩形，也即A可以將一組正交基對映到另一組正交基！那麼現在來分析：對任意M*N的矩陣，能否找到一組正交基使得經過它變換後還是正交基？答案是肯定的，它就是SVD分解的精髓所在。
現在假設存在M*N矩陣A，事實上，A矩陣將n維空間中的向量對映到k（k<=m）維空間中，k=Rank(A)。現在的目標就是：在n維空間中找一組正交基，使得經過A變換後還是正交的。假設已經找到這樣一組正交基：
{v1，v2，v3，…，vn}
則A矩陣將這組基對映為：
{Av1，Av2，Av3，…，Avn}
如果要使他們兩兩正交，即:
Avi · Avj = (Avi)TAvj = viTATAvj = 0
根據假設，存在:
viTvj = vivj = 0
所以如果正交基v選擇為ATA的特徵向量的話，由於ATA是對稱陣，v之間兩兩正交，那麼: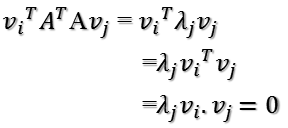 
這樣就找到了正交基使其對映後還是正交基了，現在，將對映後的正交基單位化,因為：
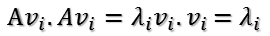
所以有：
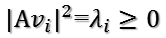
所以取單位向量：
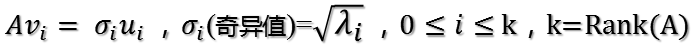
當k < i <= m時，對u1，u2，…，uk進行擴充套件u(k+1),…,um，使得u1，u2，…，um為m維空間中的一組正交基，即將{u1，u2，…，uk}正交基擴充套件成{u1，u2，…，um}Rm空間的單位正交基，同樣的，對v1，v2，…，vk進行擴充套件v(k+1),…,vn（這n-k個向量存在於A的零空間中，即Ax=0的解空間的基），使得v1，v2，…，vn為n維空間中的一組正交基，即：
在A的零空間中選擇{vk+1，vk+2，…，vn}使得AvI = 0，i > k並取σ = 0則可得到：
繼而得到A矩陣的奇異值分解：
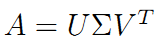
V是n*n的正交矩陣，U是m*m的正交矩陣，Σ是m*n的對角陣
現在可以來對A矩陣的對映過程進行分析了：如果在n維空間中找到一個（超）矩形，其邊都落在ATA的特徵向量的方向上，那麼經過A變換後的形狀仍然為（超）矩形！
vi為ATA的特徵向量，稱為A的右奇異向量，ui=Avi實際上為AAT的特徵向量，稱為A的左奇異向量。下面利用SVD證明文章一開始的滿秩分解：
利用矩陣分塊乘法展開得：
可以看到第二項為0，有:
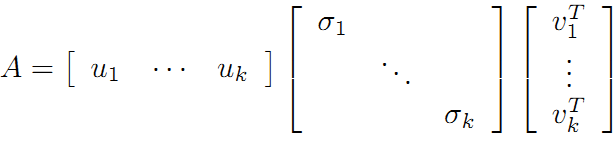
令：
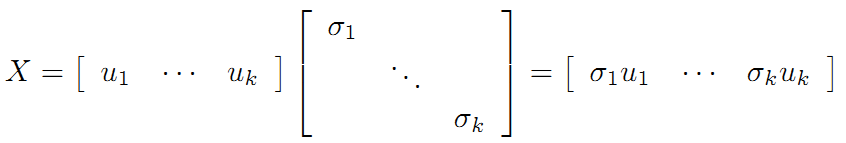
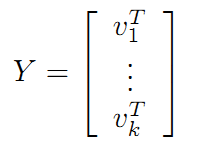
在《數學之美》上面有驗證U、V都是酉矩陣。
則A=XY即是A的滿秩分解。
2. 張量（Tucker）分解
張量：一般一維陣列，我們稱之為向量（vector）,二維陣列，我們稱之為矩陣（matrix）;三維陣列以及多位陣列，我們稱之為張量（tensor）。
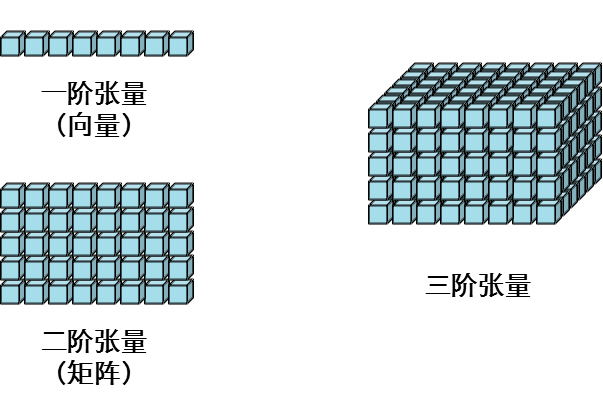
張量的知識點可參看大佬部落格：張量
2.1 CP 分解( Canonical Polyadic Decomposition (CPD)
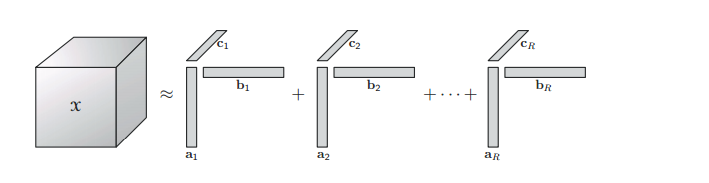
CP分解的知識點可參看大佬部落格：CP分解
2.2 TD 分解( Tucker Decomposition )
Tucker分解是一種高階的主成分分析，它將一個張量表示成一個核心（core）張量沿每一個mode乘上一個矩陣。
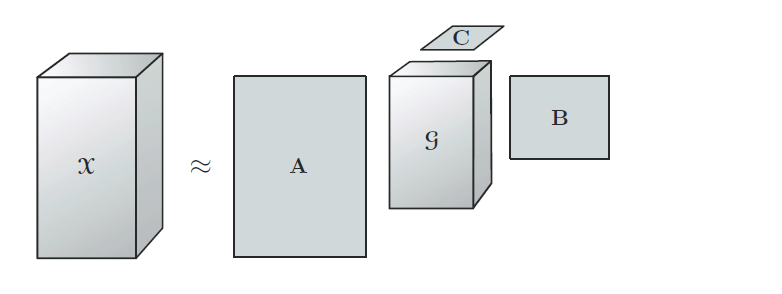
內容可參看大佬部落格：張量分解-Tucker分解
2.3 BTD 分解（block term decomposition）
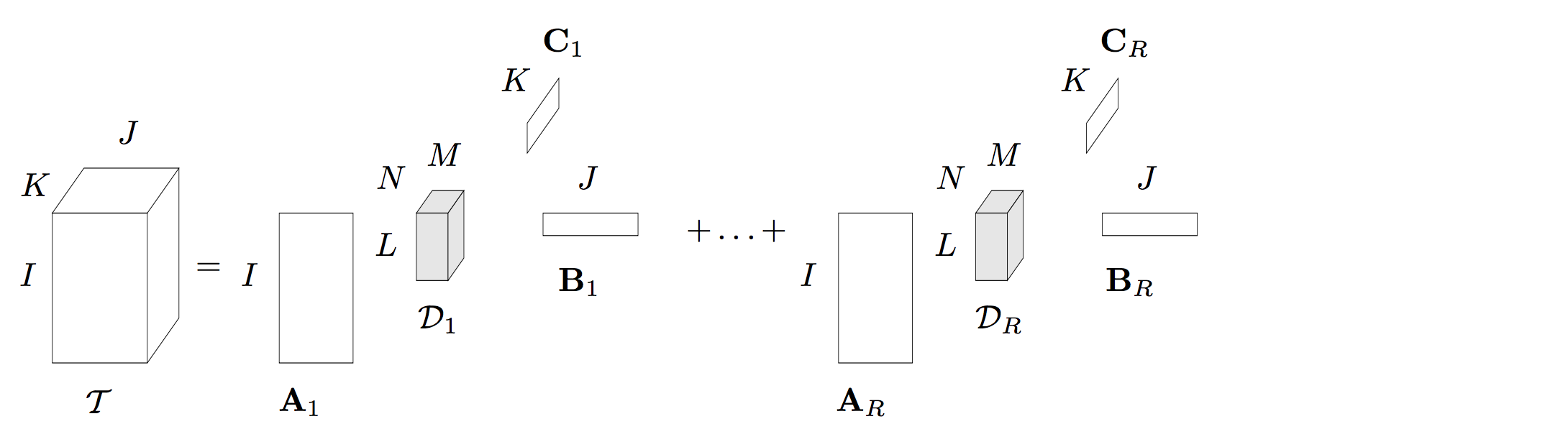
BTD的內容可參考大佬部落格：BTD分解
總結：低秩逼近的方法用於全連線層效果較好，但是對執行時間提升空間不是很大。一般能達到1.5倍。將低秩逼近的壓縮演算法用於卷積層時，會出現誤差累積的效果，對最後精度損失影像較大，需要對網路進行逐層的微調，費時費力。
知識應該是開源的，歡迎斧正，[email protected]