填個幻方如何?
轉自https://www.cnblogs.com/codingmylife/archive/2010/12/24/1915728.html
按目前填寫幻方的方法,是把幻方分成了三類,即奇數階幻方、雙偶階幻方、單偶階幻方。下面按這三類幻方,列出最常用解法。
奇數階幻方(羅伯法)
奇數階幻方最經典的填法是羅伯法。填寫的方法是:
把1(或最小的數)放在第一行正中; 按以下規律排列剩下的(n×n-1)個數:
1、每一個數放在前一個數的右上一格;
2、如果這個數所要放的格已經超出了頂行那麼就把它放在底行,仍然要放在右一列;
3、如果這個數所要放的格已經超出了最右列那麼就把它放在最左列,仍然要放在上一行;
4、如果這個數所要放的格已經超出了頂行且超出了最右列,那麼就把它放在前一個數的下一行同一列的格內;
5、如果這個數所要放的格已經有數填入,那麼就把它放在前一個數的下一行同一列的格內。
例,用該填法獲得的5階幻方:
雙偶數階幻方(對稱交換法)
所謂雙偶階幻方就是當n可以被4整除時的偶階幻方,即4K階幻方。在說解法之前我們先說明一個“互補數”定義:就是在 n 階幻方中,如果兩個數的和等於幻方中最大的數與 1 的和(即 n×n+1),我們稱它們為一對互補數 。如在三階幻方中,每一對和為 10 的數,是一對互補數 ;在四階幻方中,每一對和為 17 的數,是一對互補數 。
雙偶數階幻方的對稱交換解法:
先看看4階幻方的填法:將數字從左到右、從上到下按順序填寫:
內外四個角對角上互補的數相易,(方陣分為兩個正方形,外大內小,然後把大正方形的四個對角上的數字對換,小正方形四個對角上的數字對換)即(1,16)(4,13)互換(6,11)(7,10)互換即可。
對於n=4k階幻方,我們先把數字按順序填寫。寫好後,按4×4把它劃分成k×k個方陣。因為n是4的倍數,一定能用4×4的小方陣分割。然後把每個小方陣的對角線,象製作4階幻方的方法一樣,對角線上的數字換成互補的數字,就構成幻方。
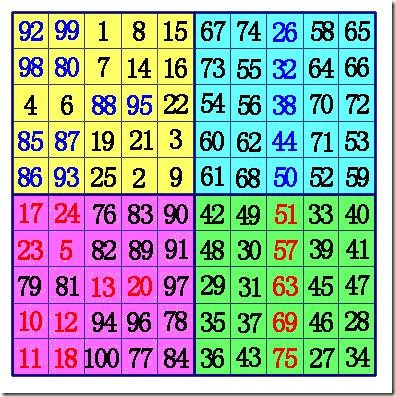
以8階幻方為例:
(1) 先把數字按順序填。然後,按4×4把它分割成4塊(如圖)
(2) 每個小方陣對角線上的數字(如左上角小方陣部分),換成和它互補的數。
單偶數階幻方(象限對稱交換法)
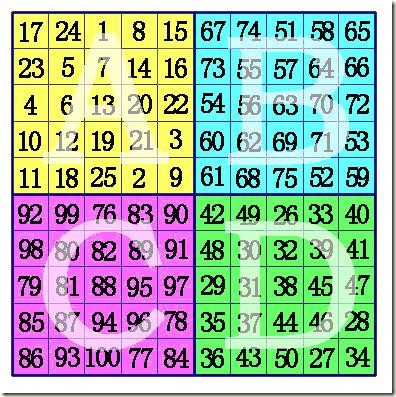
以n=10
(1)把方陣分為A,B,C,D四個象限,這樣每一個象限肯定是奇數階。用羅伯法,依次在A象限,D象限,B象限,C象限按奇數階幻方的填法填數。
(2)在A象限的中間行、中間格開始,按自左向右的方向,標出k格。A象限的其它行則標出最左邊的k格。將這些格,和C象限相對位置上的數,互換位置。
(3)在B象限任一行的中間格,自右向左,標出k-1列。(注:6階幻方由於k-1=0,所以不用再作B、D象限的資料交換), 將B象限標出的這些數,和D象限相對位置上的數進行交換,就形成幻方。
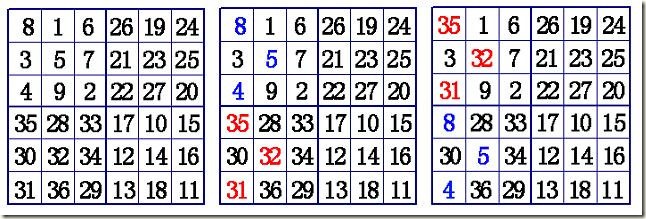
下面是6階幻方的填法:6=4×1+2,這時k=1