邏輯迴歸(logistics regression)

阿新 • • 發佈：2018-11-23

邏輯迴歸(logistics regression)

前幾章分別講了多元線性迴歸的推理思路和求解過程(解析解求解和梯度下降求解),文章並不以程式碼和公式推導過程為重點,目的是跟大家一起理解演算法.前兩章的內容是學習演算法的基礎,所以本章會在前兩章的基礎上討論邏輯迴歸(logistics regression).邏輯迴歸也屬於有監督機器學習.

之前我們瞭解到了多元線性迴歸是用線性的關係來擬合一個事情的發生規律,找到這個規律的表達公式,將得到的資料帶入公式以用來實現預測的目的,我們習慣將這類預測未來的問題稱作迴歸問題.機器學習中按照目的不同可以分為兩大類:迴歸和分類.今天我們一起討論的邏輯迴歸就可以用來完成分類任務.

一.分類和迴歸任務的區別

我們可以按照任務的種類,將任務分為迴歸任務和分類任務.那這兩者的區別是什麼呢?按照較官方些的說法,輸入變數與輸出變數均為連續變數的預測問題是迴歸問題,輸出變數為有限個離散變數的預測問題成為分類問題.

通俗一點講,我們要預測的結果是一個數,比如要通過一個人的飲食預測一個人的體重,體重的值可以有無限多個,有的人50kg,有的人51kg,在50和51之間也有無限多個數.這種預測結果是某一個確定數,而具體是哪個數有無限多種可能的問題,我們會訓練出一個模型,傳入引數後得到這個確定的數,這類問題我們稱為迴歸問題.預測的這個變數(體重)因為有無限多種可能,在數軸上是連續的,所以我們稱這種變數為連續變數.

我們要預測一個人身體健康或者不健康,預測會得癌症或者不會得癌症,預測他是水瓶座,天蠍座還是射手座,這種結果只有幾個值或者多個值的問題,我們可以把每個值都當做一類,預測物件到底屬於哪一類.這樣的問題稱為分類問題.如果一個分類問題的結果只有兩個,比如"是"和"不是"兩個結果,我們把結果為"是"的樣例資料稱為"正例",講結果為"不是"的樣例資料稱為"負例",對應的,這種結果的變數稱為離散型變數.

二.邏輯迴歸不是迴歸

從名字來理解邏輯迴歸.在邏輯迴歸中,邏輯一詞是logistics

[lə'dʒɪstɪks]的音譯字,並不是因為這個演算法是突出邏輯的特性.

至於迴歸,我們前一段講到迴歸任務是結果為連續型變數的任務,logistics regression是用來做分類任務的,為什麼叫回歸呢?那我們是不是可以假設,邏輯迴歸就是用迴歸的辦法來做分類的呢.跟上思路.

三.如果是你,你要怎麼做

假設剛剛的思路是正確的,邏輯迴歸就是在用迴歸的辦法做分類任務,那有什麼辦法可以做到呢,此時我們就先考慮最簡單的二分類,結果是正例或者負例的任務.

按照多元線性迴歸的思路,我們可以先對這個任務進行線性迴歸,學習出這個事情結果的規律,比如根據人的飲食,作息,工作和生存環境等條件預測一個人"有"或者"沒有"得惡性腫瘤,可以先通過迴歸任務來預測人體內腫瘤的大小,取一個平均值作為閾值,假如平均值為y,腫瘤大小超過y為噁心腫瘤,無腫瘤或大小小於y的,為非惡性.這樣通過線性迴歸加設定閾值的辦法,就可以完成一個簡單的二分類任務.如下圖:

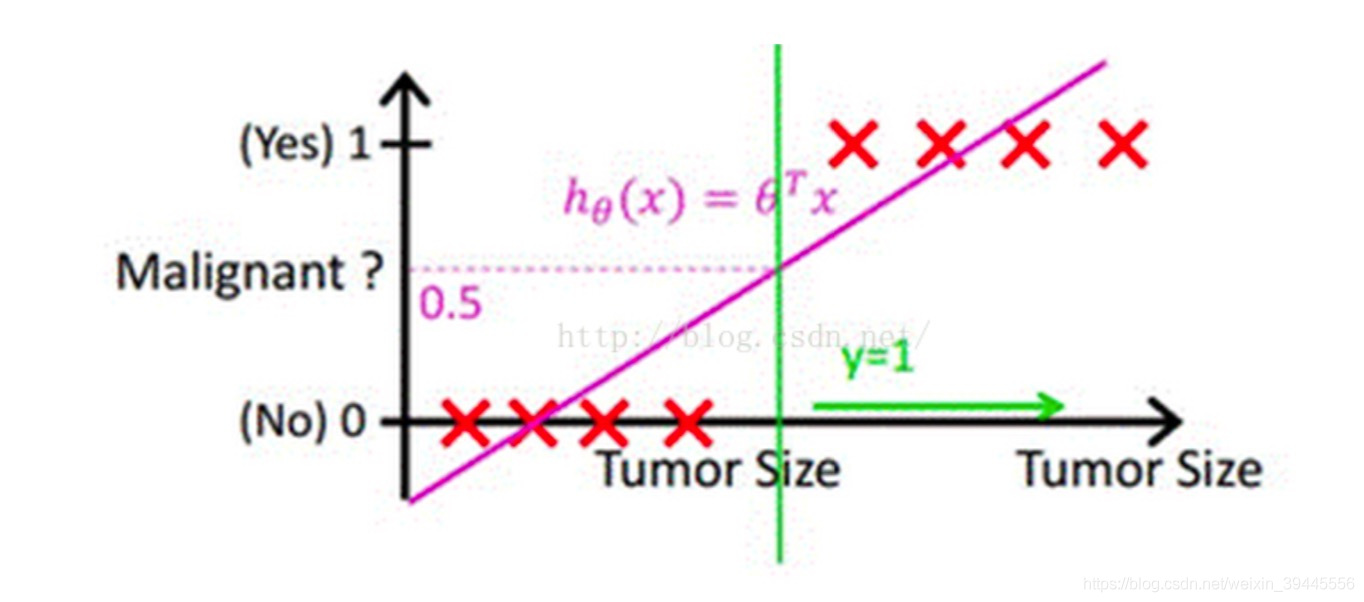
上圖中,紅色的x軸為腫瘤大小,粉色的線為迴歸出的函式 $h_{\Theta }(x)$ 的影象,綠色的線為閾值.

預測腫瘤大小還是一個迴歸問題,得到的結果(腫瘤的大小)也是一個連續型變數.通過設定閾值,就成功將回歸問題轉化為了分類問題.但是,這樣做還存在一個問題.

我們上面的假設,依賴於所有的腫瘤大小都不會特別離譜,如果有一個超大的腫瘤在我們的例子中,閾值就很難設定.加入還是取平均大小為閾值,則會出現下圖的情況:

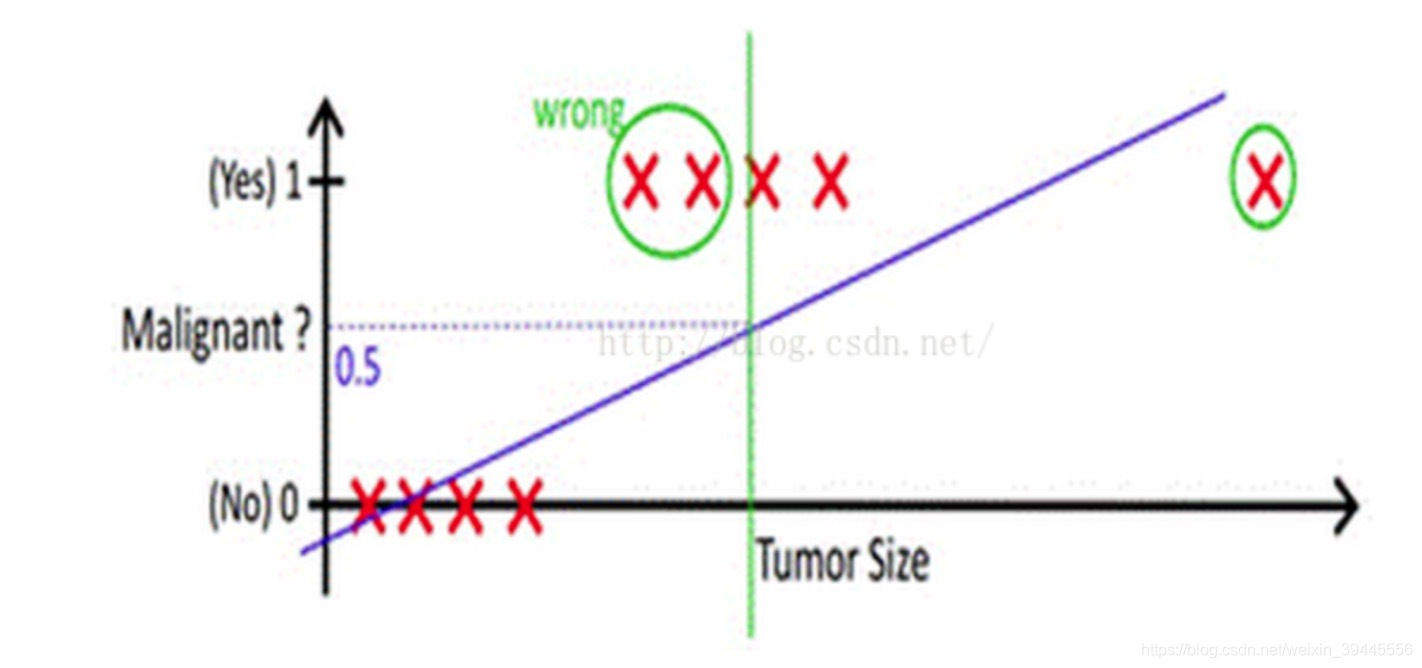
從上邊的例子可以看出,使用線性的函式來擬合規律後取閾值的辦法是行不通的,行不通的原因在於擬合的函式太直,離群值(也叫異常值)對結果的影響過大,但是我們的整體思路是沒有錯的,錯的是用了太"直"的擬合函式,如果我們用來擬合的函式是非線性的,不這麼直,是不是就好一些呢?

所以我們下面來做兩件事:

1-找到一個辦法解決掉迴歸的函式嚴重受離群值影響的辦法.

2-選定一個閾值.

四:把迴歸函式掰彎

沒錯,本小節用來解決上邊說的第一個問題.開玩笑了,無論如何我也不可能掰彎這個函式.我們能做的呢,就是換一個.原來的判別函式我們用線性的y = $w^{T}x$ ,邏輯迴歸的函式呢,我們目前就用sigmod函式,函式如下:

公式中,e為尤拉常數(是常數,如果不知道,自行百度),Z就是我們熟悉的多元線性迴歸中的 $W^{T}X$ ,建議現階段大家先記住邏輯迴歸的判別函式用它就好了.如果你不服,請參考:朱先生1994的部落格(部落格講的很好).

就像我們說多元線性迴歸的判別函式為 $y = w_{0}x_{0} + w_{1}x_{1} + ... +w_{n}x_{n}$ 一樣.追究為什麼是他花費的經歷會比演算法本身更多.

sigmod函式的影象如下:

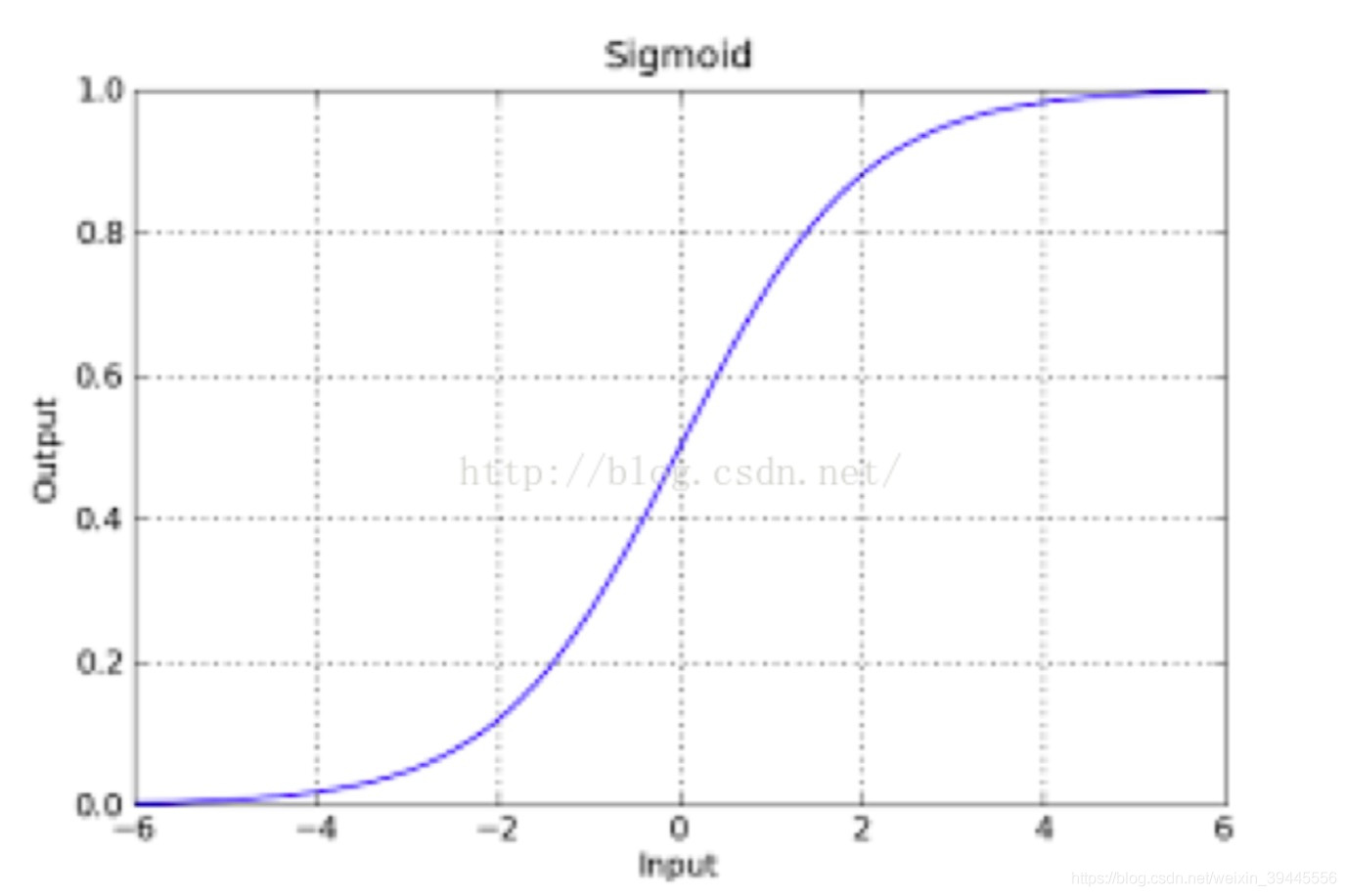
該函式具有很強的魯棒性(魯棒是Robust的音譯，也就是健壯和強壯的意思),並且將函式的輸入範圍(∞,-∞)對映到了輸出的(0,1)之間且具有概率意義.具有概率意義是怎麼理解呢:將一個樣本輸入到我們學習到的函式中,輸出0.7,意思就是這個樣本有70%的概率是正例,1-70%就是30%的概率為負例.

再次強調一下,如果你的數學功底很好,可以看一下我上邊分享的為什麼是sigmod函式的連線,如果數學一般,我們這個時候沒有必要糾結為什麼是sigmod,函式那麼多為什麼選他.學習到後邊你自然就理解了.

總結一下上邊所講:我們利用線性迴歸的辦法來擬合然後設定閾值的辦法容易受到離群值的影響,sigmod函式可以有效的幫助我們解決這一個問題,所以我們只要在擬合的時候把 $y = w_{0}x_{0} + w_{1}x_{1} + ... +w_{n}x_{n}$ 即y = $W^{T}X$ 換成 $g(z) = \frac{1}{1+e^{-z}}$ 即可,其中

z= $W^{T}X$ ,也就是說g(z) = $\frac{1}{1 + e^{w^{T}x}}$ . 同時,因為g(z)函式的特性,它輸出的結果也不再是預測結果,而是一個值預測為正例的概率,預測為負例的概率就是1-g(z).

函式形式表達:

P(y=0|w,x) = 1 – g(z)

P(y=1|w,x) = g(z)

P(正確) = $(g(w,xi))^{y^{i}}$ * $(1-g(w,xi))^{1-y^{i}}$ $y^{i}$ 為某一條樣本的預測值,取值範圍為0或者1.

到這裡,我們得到一個迴歸函式,它不再像y=wT * x一樣受離群值影響,他的輸出結果是樣本預測為正例的概率(0到1之間的小數).我們接下來解決第二個問題:選定一個閾值.

五:選定閾值

選定閾值的意思就是,當我選閾值為0.5,那麼小於0.5的一定是負例,哪怕他是0.49.此時我們判斷一個樣本為負例一定是準確的嗎?其實不一定,因為它還是有49%的概率為正利的.但是即便他是正例的概率為0.1,我們隨機選擇1w個樣本來做預測,還是會有接近100個預測它是負例結果它實際是正例的誤差.無論怎麼選,誤差都是存在的.所以我們選定閾值的時候就是在選擇可以接受誤差的程度.

我們現在知道了sigmod函式預測結果為一個0到1之間的小數,選定閾值的第一反應,大多都是選0.5,其實實際工作中並不一定是0.5,閾值的設定往往是根據實際情況來判斷的.本小節我們只舉例讓大家理解為什麼不完全是0.5,並不會有一個萬能的答案,都是根據實際工作情況來定的.

0到1之間的數閾值選作0.5當然是看著最舒服的,可是假設此時我們的業務是像前邊的例子一樣,做一個腫瘤的良性惡性判斷.選定閾值為0.5就意味著,如果一個患者得惡性腫瘤的概率為0.49,模型依舊認為他沒有患惡性腫瘤,結果就是造成了嚴重的醫療事故.此類情況我們應該將閾值設定的小一些.閾值設定的小,加入0.3,一個人患惡性腫瘤的概率超過0.3我們的演算法就會報警,造成的結果就是這個人做一個全面檢查,比起醫療事故來講,顯然這個更容易接受.

第二種情況,加入我們用來識別驗證碼,輸出的概率為這個驗證碼識別正確的概率.此時我們大可以將概率設定的高一些.因為即便識別錯了又能如何,造成的結果就是在一個session時間段內重試一次.機器識別驗證碼就是一個不斷嘗試的過程,錯誤率本身就很高.

以上兩個例子可能不大準確,只做意會,你懂了就好. [此時我的表情無法描述]

到這裡,邏輯迴歸的由來我們就基本理清楚了,現在我們知道了邏輯迴歸的判別函式就是 $g(z) = \frac{1}{1+e^{-z}}$ ,z= $W^{T}X$ .休息兩分鐘,我們下面看如何求解邏輯迴歸,也就是如何找到一組可以讓 $g(z) = \frac{1}{1+e^{-z}}$ 全都預測正確的概率最大的W.

六.最大似然估計

此時我們想要找到一組w,使函式 $g(z) = \frac{1}{1+e^{-z}}$ 正確的概率最大.而我們在上面的推理過程中已經得到每個單條樣本預測正確概率的公式:

P(正確) = $(g(w,xi))^{y^{i}}$ * $(1-g(w,xi))^{1-y^{i}}$

若想讓預測出的結果全部正確的概率最大,根據最大似然估計(多元線性迴歸推理中有講過,此處不再贅述),就是所有樣本預測正確的概率相乘得到的P(總體正確)最大,此時我們讓 ,數學表達形式如下:

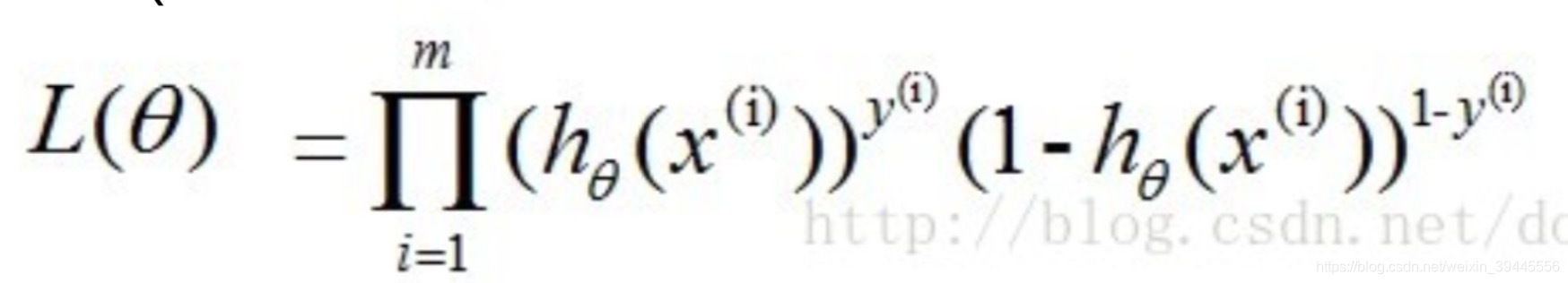
上述公式最大時公式中W的值就是我們要的最好的W.下面對公式進行求解.

我們知道,一個連乘的函式是不好計算的,我們可以通過兩邊同事取log的形式讓其變成連加.

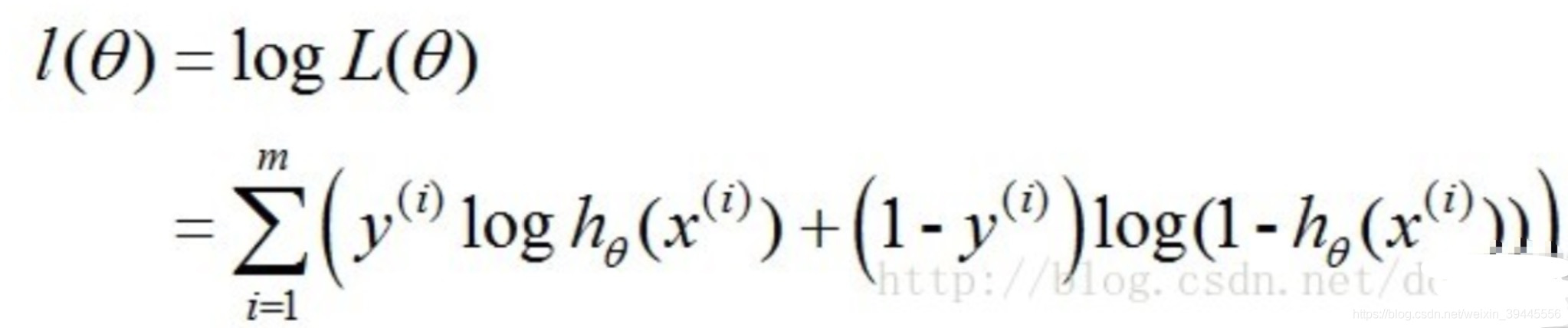
得到的這個函式越大,證明我們得到的W就越好.因為在函式最優化的時候習慣讓一個函式越小越好,所以我們在前邊加一個負號.得到公式如下:

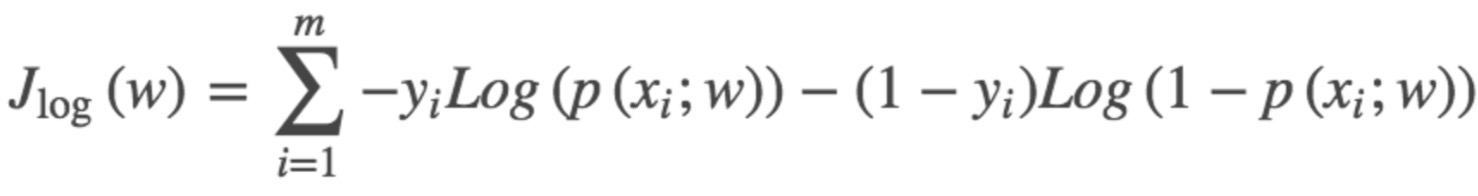
這個函式就是我們邏輯迴歸(logistics regression)的損失函式,我們叫它交叉熵損失函式.

七.求解交叉熵損失函式

求解損失函式的辦法我們還是使用梯度下降,同樣在批量梯度下降與隨機梯度下降一節有詳細寫到,此處我們只做簡要概括.

求解步驟如下:

1-隨機一組W.

2-將W帶入交叉熵損失函式,讓得到的點沿著負梯度的方向移動.

3-迴圈第二步.

求解梯度部分同樣是對損失函式求偏導,過程如下:

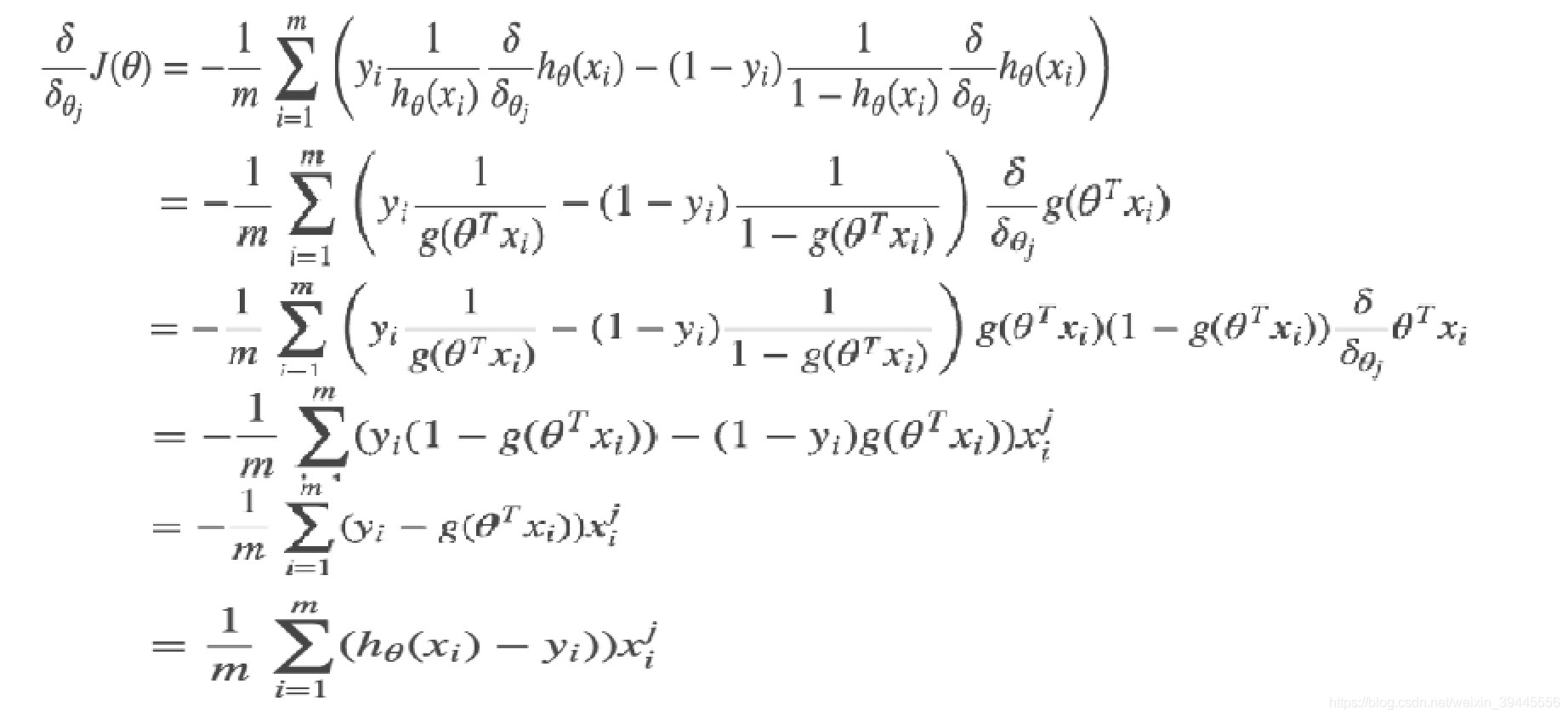
交叉熵損失函式的梯度和最小二乘的梯度形式上完全相同,區別在於,此時的 $h_{\Theta}(x) = g(z)$ ,而最小二乘的 $h_{\Theta} = W^{T}X$ .

到這裡,邏輯迴歸就講解完畢了.請大家幫忙勘誤,共同學習.

邏輯迴歸(logistics regression)