對稱性在積分中可以說是一個非常重要的問題，可以為解題帶來很大的簡便。對於不同的積分對稱性的使用也是不一樣的，最特殊的應該是第二型曲面積分。偶0奇倍。

還有對於第一型曲面積分來說，投影前通常要考慮投影是否重合的問題，此處用到的也是對稱性。

本篇文章專注於二重積分中對稱性的探討，並給出幾道經典的題目作為結尾。

1.普通對稱性

對於普通對稱性，觀察積分割槽域與被積函式的關係。

若現在的積分割槽域是關於y軸對稱，也就是關於字母x,則考察被積函式中x是否是奇函式還是偶函式，偶倍奇零。

若現在積分割槽間是關於x軸對稱，則考察字母y的關係

若現在積分割槽間關於原點對稱，也就是關於x,y都是奇函式，看兩個字母都可。

該是最簡單也最常用的一種對稱性。

2.輪換對稱性：考慮積分割槽域關於y=x對稱，則對於被積函式f(x,y)和f（y,x）是等價的，此時不用考慮f 對稱。

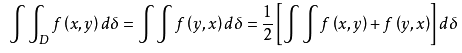
此處的解釋就是說當換完字母后，積分割槽間不變，相當於對座標系重新命名

3.這個對稱性我還不知道叫什麼，只能先這樣了

如果積分割槽域與被積函式均關於y=x對稱，則原來在整個區間上的積分=2*半個區間上的積分。