HDU 3668 View Code (二重積分)
阿新 • • 發佈:2019-01-04
大體題意:
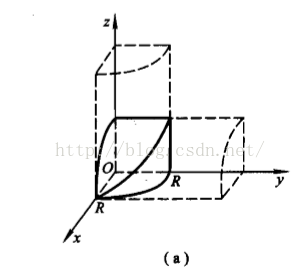
求圖中交叉圓柱體的體積!
思路:
真是充分反映了高數能力! 是真弱啊,,想了6,7個小時了,才想明白! = =T_T!!!!
大體思路很明確,把兩個圓柱的體積加起來 減去中間公共部分的即可!
第一步首先得想到公共部分是一個怎樣的圖形。
這個在高數下冊例題中有講到!
中間實線部分就是第一卦限內的圖形,顯然一個二重積分就可以搞定:
這種情況比較簡單點,適合於2*R <= h 的時候!
如果2*R > h話!
需要加點想象力,中間公共部分 是一個長方體 加上兩個小突起
也是把他分成8份,只算第一卦限內的。
把他放到座標系裡 與上一個圖相比,沒什麼變換 只是將上一個圖沿x軸平移了h/2 個單位,而0~h/2這片區域是一個長方體!
這樣只需改變積分上下限即可!公式不變!(這裡想了很久)
詳細見程式碼:
#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; const double eps = 1e-8; const double pi = acos(-1.0); int main(){ double r,h; while(scanf("%lf %lf",&r,&h) == 2){ if (2*r > h + eps){ double a = sqrt(r*r-h*h/4); // printf("%lf\n",a); double V = 2*pi*r*r*h; double other = h*h*a/4 + r*r*r*2/3 + (a)*(a)*(a)/3 - r*r*a; double ans = V-8.0*other; printf("%.4lf\n",ans+eps); }else{ double V = 2*pi*r*r*h; double other = 8*2*r*r*r/3; double ans = V-other; printf("%.4lf\n",ans+eps); } } return 0; }