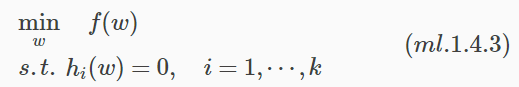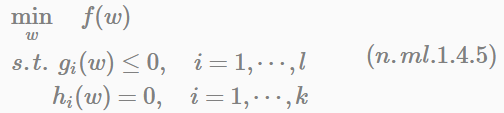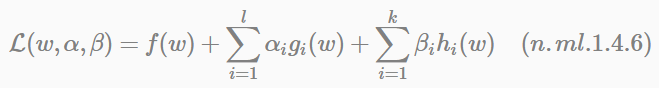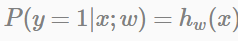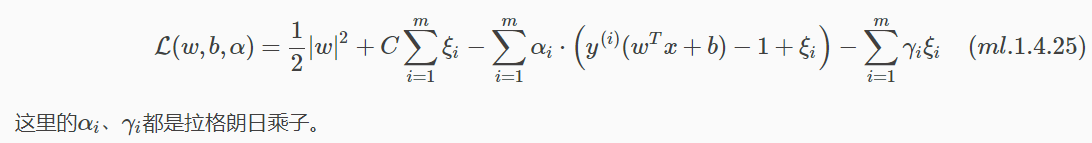寫在前面

機器學習中有這樣一個結論：低維空間線性不可分的資料通過非線性對映到高維特徵空間則可能線性可分。極端地，假設資料集中有m個樣本，一定可以在m−1維空間中線性可分。

每一個樣本在特徵空間中對應一個點，試想一下，2個點可以用一維空間分開；3個點可以在2維空間（平面）上線性可分；… ；m個點，可以在m−1維空間中線性可分。

高維空間可以讓樣本線性可分，這固然是優點。但是如果直接採用非線性對映技術在高維空間進行一個學習任務（如分類或迴歸），則需要確定非線性對映函式的形式和引數、高維特徵空間維數等問題；而最大的問題在於在高維特徵空間運算時可能存在的“維數災難“。

本章要介紹的核函式方法可以有效地解決這類問題。這裡先給出核函式工作的基本思路：

從上式可以看出，核函式將n維高維特徵空間的內積計算轉化為k維低維輸入空間的核函式計算，巧妙地解決了在高維特徵空間中計算可能出現的“維數災難”等問題。從而為高維特徵空間解決複雜的學習問題奠定了理論基礎。

本章的安排是這樣。首先介紹一些對偶優化問題的基本形式，引出核函式並且為後面的SVM做鋪墊；然後給出核函式的發展、常用的核函式等方法；最後詳細介紹核函式在分類方法中的經典應用－支援向量機。

對偶優化問題

我們都知道，機器學習模型引數學習過程，大多要通過《最優化演算法》中的一些方法來求解。其中，帶約束條件的最優化問題（極值求解問題）一般是引入拉格朗日乘子法，構建拉格朗日對偶函式，通過求其對偶函式的解，從而得到原始問題的最優解。

其實不僅是帶約束的最優化問題，任何一個最優化問題都伴隨著一個”影子”最優化問題。其中一個稱為原始問題，另一個稱為對偶問題。

這裡，先以迴歸模型的目標函式為例，給出其對偶形式；然後在簡要描述帶約束的最優化問題求解的一般思路，引出核函式。

無約束優化問題的對偶形式

迴歸模型的目標函式：


公式(ml.1.4.4)是一個表示任意兩個樣本之間關係的函式。後面會提到，每一個玉樹值可通過定義核函式來計算。

約束優化問題求解一般思路

拉格朗日乘子（Lagrange Multiplier）
拉格朗日乘子法通常用於求解帶等式約束的極值問題，一個典型的最優化問題形式化表示如下：


為什麼引入拉格朗日乘子就可以求解出極值？

主要原因是f(w)的切線方向（dw變化方向）受其它等式的約束，dw的變化方向與f(w)的梯度方向垂直時才能獲得極值。並且在極值點處，f(w)的梯度與其它等式梯度的線性組合平行。因此它們之間存線上性關係。具體可參考《最優化演算法》系列。

拉格朗日對偶（Lagrange Duality）

對於帶有不等式約束的極值問題，形式化表示如下：

定義拉格朗日公式：

公式(n.ml.1.4.6)中的αi和βi都是拉格朗日乘子。但如果按照該公式求解會出現以下問題。

首先面對兩個引數α、β，並且引數αi也是一個不等式約束；然後再在w上求極小值。這個過程不容易做，可否有相對容易的解法呢？

核方法

在機器學習中，核方法被形式化為特徵空間的向量內積。又被稱為核技巧（kernel trick），或核置換（kernel substitution）。

核函式介紹

早在機器學習學科成立之前，核函式相關理論、核函式技術以及核函式的有效性定理就已經存在。1964年Aizerman等人把勢函式（potential function）相關研究引入到模式識別領域。中間過去很多年，直到1992年Boser等人在研究機器學習中最大間隔分類器中再次將核函式引入進來，產生了支援向量機技術。從這開始，核函式在機器學習的理論和應用得到了更多地關注和極大的興趣。

例如，Scholkopf等人將核函式應用到主成分分析PCA中產生了核主元分析法（kernel PCA），Mika等人將核函式引入到Fisher判別中產生了核Fisher判別分析（kernel Fisher discriminant）等等。這些技術在機器學習、模式識別等不同領域中起到了很重要的作用。

核函式有效性Mercer定理可追溯至1909年。

核函式引入

Andrew Ng男神在《機器學習》課程第一講的線性迴歸中提到例子，用迴歸模型擬合房屋面積（x表示）與價格（y表示）之間的關係。示例中的迴歸模型用y=w0+w1x方程擬合。假設從樣本的分佈中可以看到x與y符合3次曲線關係，那麼我們希望使用x的3次多項式來逼近這些樣本點。

我們希望將對映後的特徵應用於後面要介紹的SVM分類中，而不直接用原始特徵（Raw Feature）。

為什麼要用對映後的特徵，而不是原始特徵來計算呢?

為了更好的擬合數據是其中一個原因。另外一個重要原因是本章寫在前面提到的：樣本可能存在在低維空間線性不可分的情況，而將其對映到高維空間中往往就可分。

核函式方法

上式稱為Sigmoid核函式（sigmoidal kenel）。Sigmoid核多用於多層感知機神經網路，隱含層節點數目、隱含節點對輸入節點的權值都是在訓練過程中自動確定。

注意：sigmoid核對應的核函式矩陣不是正定的。之所以仍作為kernel的一種是因為給了kernel在實際應用中更多的擴充套件，包括在svm、神經網路等方法中的應用。

核函式有效性判定

問題：

Mercer定理

在介紹Mercer定理之前，我們先解決上面的問題：

可見，核函式矩陣K應該是個對稱陣。下面的公式推導會給出更明確的結論。

如此，我們可以得出核函式的必要條件是：

K是有效的核函式 ⟹ 核函式矩陣K半正定。

比較幸運的是，這個條件也是充分的。具體由Mercer定理來表達:

Mercer定理：

Mercer定理可以說明：為了證明K是有效的核函式，我們不用直接去尋找ϕ，只需要在訓練集上求出各個Kij，然後判定矩陣K是否是半正定即可。

注：使用矩陣左上角主子式 ≥0等方法可判定矩陣是否是半正定的。

當然，Mercer定理證明過程中可以通過L2範數和再生希爾伯特空間等概念，但在n維情況下，這裡給出的證明是等價的。

Kernel方法不僅用在SVM上，只要在模型的計算過程中出現⟨x,z⟩，我們都可以使用K(x,z)去替換，通過特徵空間變換解決本章開頭所提到的特徵對映問題。

支援向量機

支援向量機（Support Vector Machine，簡稱SVM）是建立在統計學習理論之上的學習演算法，其主要優勢體現在解決線性不可分問題，通過引入核函式，巧妙地解決了在高維空間的內積運算複雜度的問題，從而很好的解決了非線性分類問題。

這裡我們先通過LR模型與SVM比較，建立二者之間的基本認知。

LR與SVM

LR模型將特徵的線性組合作為自變數（取值範圍(−∞,∞)），使用logistic函式（又稱sigmoid函式）將自變數對映到(0,1)上，對映後的值被認為是y=1的概率（如果是分類問題），表示式


LogReg模型要用全部訓練資料學習引數w，學習過程中儘可能使正樣本的特徵組合遠大於0，負樣本的特徵組合遠小於0。

注意：LR強調的是在全部訓練樣本上達到這個目標，採用MLE作為求參準則

SVM直觀引入

函式間隔與幾何間隔

形式化表示

函式間隔（Functional Margin）

即全域性函式間隔就是在所有訓練樣本上分類正例和負例確信度最小的那個函式間隔。

幾何間隔（Geometric Margin）

主要考查點：

在我們廣告演算法組的相關面試中，經常會請求職者推導n維空間中點到超平面的距離公式（如果求職者知道SVM），但是能完整推匯出來的只有十之二三 …

幾何間隔在分類問題中，可表示為：

最優間隔分類器

在前面也提到，SVM的目標是尋找一個超平面，使得距離超平面最近的點能有更大的間距。不考慮所有的點都必須遠離超平面，只關心求得的超平面能夠讓所有的點中離它最近的點具有最大間距。因此，我們需要數學化表示最優間隔（optimal margin classifier）。

形式化表示

最優間隔形式化可表示為：

然而此時的目標函式仍然不是凸函式，無法方便求解。繼續改寫目標函式…

公式(ml.1.4.17)是一個典型的帶不等式約束的二次規劃求解問題（目標函式是自變數的二次函式）。

到此為止，我們完成了目標函式由非凸到凸的轉變。

最優間隔分類器學習過程

KKT條件

這個KKT雙重補足條件會用來解釋SVM中的支援向量和SMO的收斂測試。KKT思想可總結如下：KKT總體思想是認為極值會在可行域邊界上取得，也就是不等式為0或等式約束的條件下取得，而最優下降（或上升）方向一般是這些等式的線性組合，其中每個元素要麼是不等式為0的約束，要麼是等式約束。對於在可行域邊界內的點，對目標函式最優解不起作用，因此前面的係數為0 。

優化目標
重新前面的SVM的優化問題：

SVM對偶問題

下面我們看著拉格朗日的對偶問題來求解，對偶函式表示式如下：

將公式(n.ml.1.4.20)帶入(ml.1.4.18)，此時得到的是該目標函式的最小部分（因為目標函式是凸函式）。公式推導如下：

接著，求極大化過程。此時極值問題可表示為：

對偶問題求解思路

上面的討論都是建立在樣本線性可分的假設前提下，當樣本不可分時，我們可以嘗試利用核函式將特徵對映到高維空間，這樣很可能就可分了。然而，對映後也不能保證樣本100%線性可分，那又該如何？這就是下面通過引入鬆弛變數的軟間隔模型和正則化要解決的問題。

軟間隔與正則化

為了解決上述問題，這裡需要將模型做一個調整，以保證在不可分的情況下，也能夠儘可能地找出分隔超平面。

軟間隔與懲罰項

引入鬆弛變數就是允許樣本點的函式間隔小於1，即在最大間隔區間裡面，或者函式間隔可以為負數，即樣本點在對方的區域中。

我們可以給出以下總結：
目標函式控制了離群點的資料和程度，使大部分樣本點仍然遵守限制條件。同時，考慮了離群點對模型的影響。
模型修改後，同時也需要對(ml.1.4.19)拉格朗日公式進行修改如下：

回想4.1.4節中介紹的拉格朗日對偶中提到的求法。

1. 首先，寫出拉格朗日公式（如(ml.1.4.25)）；
2. 然後，將其看作是變數w和b的函式，分別對其求偏導，得到w和b的表示式；
3. 最後，把表示式帶入拉格朗日公式中，求帶入公式後的極大值。

整體推導過程如4.1.5節類似，這裡只給出最後結果：

公式(ml.1.4.27)第(1)式子表明，在兩條間隔線外的樣本點前面的係數為0；第(2)個式子表明，在間隔線內的樣本點（離群點）前面的係數為C；第(3)個式子表明，支援向量（即在超平面兩邊的最大間隔線上）的樣本想前面係數在(0,C)上。

通過KKT條件剋制，某些在最大間隔線上的樣本點也不是支援向量，相反可能是離群點（(1)、(2)中等號成立時）。

SMO演算法（Sequential Minimal Optimization）用於求解目標函式W(α)的極大值。