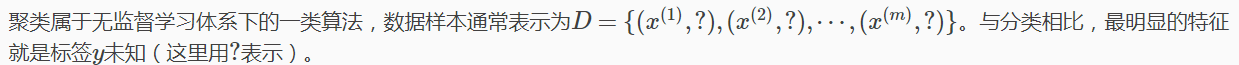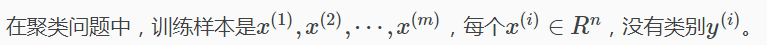深入淺出ML之Clustering家族
寫在前面
那麼如何把相近的樣本點聚合在一起,同樣不相近的樣本儘可能不在同一個簇中?一個思路就是假設每個樣本有標籤,只是“隱藏”起來了,把它當作隱變數(latent variable)。然後用監督學習的思路去求解,把相同標籤的樣本聚合在一起即可。
如此一來,會發現整個過程出現兩類變數:
- 樣本類別變數
- 模型引數變數
傳統的引數學習演算法無法解決該類問題,How to do it? 下面要介紹的期望最大值演算法可以很好的解決該類問題。
期望最大值演算法
期望最大值(Expectation Maximization,簡稱EM演算法)是在概率模型中尋找引數最大似然估計或者最大後驗估計的演算法,其中概率模型依賴於無法觀測的隱藏變數。
其主要思想就是通過迭代來建立完整資料的對數似然函式的期望界限,然後最大化不完整資料的對數似然函式。
本節將盡可能詳盡地描述EM演算法的原理。並結合下一節的高斯混合模型介紹EM演算法是如何求解的。
數學鋪墊
Jensen不等式
Jensen不等式表述如下:
如果f是凸函式,X是隨機變數,那麼有 E[f(X)]≥f(E[X]).
特別的,如果f是凸函式,那麼 E[f(X)]=f[E(X)]當且僅當p(x=E[X])=1,此時隨機變數X就是常量。
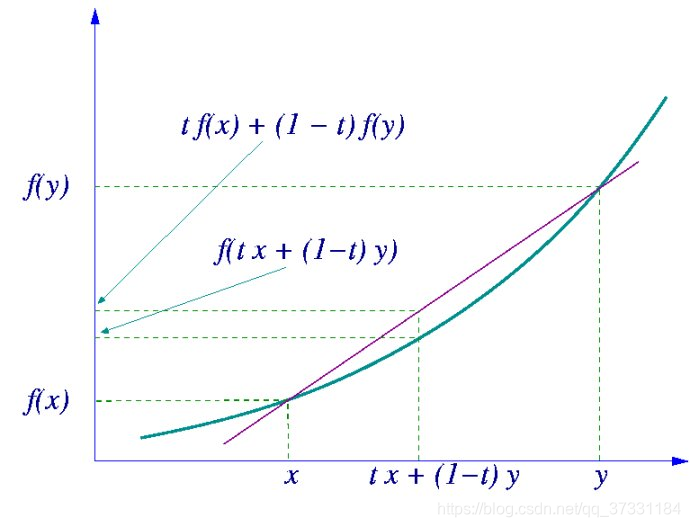
在圖中,實現f是凸函式,X是隨機變數,假設其取值為x和y(概率分別為0.5)。那麼X的期望值就是[x,y]的中值,從圖中可以看到E[f(x)]≥f(E[x])成立。
Jensen不等式同樣可應用於凹函式,不等號方向相反即可,即E[f(X)]≤f(E[X])。
EM演算法描述
EM初探
解釋公式(ml.1.10.1),首先對極大似然函式取對數,然後對每個樣本的每一種可能類別z求聯合分佈概率之和。
直接求引數w會比較困難,因為有隱變數z的存在,如果確定了z之後,再求解就容易了(不同於監督學習過程,這裡存在兩個變數:模型引數變數w和模型類別變數z)。
EM演算法是一種求解存在隱變數的引數優化問題的有效方法。既然不能直接最大化ℓ(w),我們可以不斷的建立ℓ的下界(E步),然後優化下界(M步)。
公式推導
公式(ml.1.10.2)解釋:
(1)到(2)比較直接,分子分母同乘以一個相等的函式;(2)到(3)利用了Jensen不等式。這裡面函式log(x)是凹函式(二階導數小於0),並且
E步
M步
虛擬碼中提到,直到收斂迴圈才退出。那麼如何保證收斂?這是下一節要介紹的內容。
EM演算法收斂性證明
收斂性證明
EM演算法思想總結:
高斯混合模型
密度估計(Density Estimation)是無監督學習非常重要的一個應用方向。本節主要介紹高斯混合模型(Gaussian Mixture Model,簡稱GMM)如何求解,進而做密度估計的?
GMM介紹
高斯混合模型可以描述為:
高斯混合模型與高斯判別分析
公式(ml.1.10.6)與第5章中的(ml.1.5.6)表達的是同一個意思。包括(ml.1.10.8)與(ml.1.5.7)的求解結果,在物理意義也是等價的。
GMM與GDA相同點:
- 模型的概率假設相同:類別z(i)服從多項式分佈,樣本特徵服從多變數高斯分佈;
- 目標函式一致:都是聯合概率分佈(在訓練集上)的極大似然估計
GMM與GDA不同點:
- 學習方式不同:GDA是有監督學習,而GMM用於無監督學習;
- 求解演算法不同:GDA直接通過MLE求引數偏導即可得到閉式解;GMM因為有隱變數,需要用EM演算法不斷迭代,得到結果。
GMM引數學習過程
因此用EM演算法求解高斯混合模型的步驟如下:
跟下面要介紹的經典聚類演算法K-menas相比,這裡使用類別“軟”指定,為每個樣例分配的類別z(i)是有概率分佈的,同時計算量也變大了,每個樣例i都要計算屬於每一個類別j的概率。與K-means相同的是,結果仍然是區域性最優解。對其它引數取不同的初始值進行多次計算不失為一種好方法。
K-means聚類
K-menas是聚類演算法中最經典的一個。這裡首先介紹K-means演算法的流程,然後闡述其背後包含的EM思想。
關於聚類
聚類屬於無監督學習,之前章節中的Regression,Naive Bayes,SVM等都是有類別標籤的,也就是樣本中已經給出了真實分類標籤。而聚類樣本中沒有給定標籤,只有特徵(向量)。
K-means演算法流程
K-means演算法是將樣本聚類成k個簇,演算法描述如下:
#include<iostream>
#include<cmath>
#include<vector>
#include<ctime>
using namespace std;
typedef unsigned int uint;
struct Cluster
{
vector<double> centroid;
vector<int> samples;
}
vector<Cluster> k_means(vector<vector<double> > trainX, int k, int maxepoches)
{
const int row_num = trainX.size();
const int col_num = trainX[0].size();
/*初始化聚類中心*/
vector<Cluster> clusters(k);
int seed = (int)time(NULL);
for (int i = 0; i < k; i++)
{
srand(seed);
int c = rand() % row_num;
clusters[i].centroid = trainX[c];
seed = rand();
}
......
}
然後,迭代中的每一步計算每個星星到k個質心中的每一個的距離,選取距離最近的那個星團作為\(c^{(i)}\)。
這樣經過第一步每個星星都有了所屬的星團;第二步對於每個星團,重新計算它的質心\(\mu_j\)(對裡面所有的星星座標求平均)。重複迭代第一步和第二步直至質心不變或變動很小。示例程式碼如下
vector k_means(vector > trainX, int k, int maxepoches)
{
const size_t row_num = trainX.size();
const size_t col_num = trainX[0].size();
/*初始化聚類中心*/
(在此省略)
/*多次迭代直至收斂,這裡固定迭代次數(100次)*/
for (int it = 0; it < maxepoches; it++)
{
/*每一次重新計算樣本點所屬類別之前,清空原來樣本點資訊*/
for (int i = 0; i < k; i++)
{
clusters[i].samples.clear();
}
/*求出每個樣本點距應該屬於哪一個聚類*/
for (int j = 0; j < row_num; j++)
{
/*都初始化屬於第0個聚類*/
int c = 0;
double min_distance = cal_distance(trainX[j], clusters[c].centroid);
for (int i = 1; i < k; i++)
{
double distance = cal_distance(trainX[j], clusters[i].centroid);
if (distance < min_distance)
{
min_distance = distance;
c = i;
}
}
clusters[c].samples.push_back(j);
}
/*更新聚類中心*/
for (int i = 0; i < k; i++)
{
vector<double> val(col_num, 0.0);
for (int j = 0; j < clusters[i].samples.size(); j++)
{
int sample = clusters[i].samples[j];
for (int d = 0; d < col_num; d++)
{
val[d] += trainX[sample][d];
if (j == clusters[i].samples.size() - 1)
{
clusters[i].centroid[d] = val[d] / clusters[i].samples.size();
}
}
}
}
} // 多次迭代,直至收斂
return clusters;
}
double cal_distance(vector a, vector b)
{
size_t da = a.size();
size_t db = b.size();
if (da != db)
{
cerr << "Dimensions of two vectors must be same!\n";
}
double val = 0.0;
for (size_t i = 0; i < da; i++)
{
val += pow((a[i] - b[i]), 2);
}
return pow(val, 0.5);
}
K-means收斂性
k-means面對的第一個問題是如何保證收斂,演算法描述中搶到結束條件就是收斂,可以證明的是k-means完全可以保證收斂。下面是定性的描述,先定義畸變函式(Distortion Function)如下:
K-means與EM演算法
如果我們找到的y能夠使P(x,y)最大,那麼可以說y是樣本x的最佳類別了,x歸類為y就順理成章了。但是我們第一次指定的y不一定會讓P(x,y)最大。而且P(x,y)還依賴於其它未知引數,當然在給定y的情況下,我們可以調整其它引數讓P(x,y)最大。但是調整引數後,我們發現有更好的y可以指定。那麼我們重新指定y,然後再計算P(x,y)最大時的引數,反覆迭代知道沒有更好的y可以指定。
聯合概率分佈P(x,y)最大所對應的y就是x的最佳類別。
更多案例請關注“思享會Club”公眾號或者關注思享會部落格:http://gkhelp.cn/