# 對梯度下降演算法的理解和實現 ​ 梯度下降演算法是機器學習程式中非常常見的一種引數搜尋演算法。其他常用的引數搜尋方法還有：牛頓法、座標上升法等。 ## 以線性迴歸為背景 ​ 當我們給定一組資料集合 $D=\{(\mathbf{x^{(0)}},y^{(0)}),(\mathbf{x^{(1)}},y^{(1)}),...,(\mathbf{x^{(n)}},y^{(n)})\}$ ，其中上標為樣本標記，每個 $\mathbf{x^{(i)}}$ 為一個 $d$ 維向量（向量預設加粗表示）。我們在有了一定數量的樣本的情況下，希望能夠從樣本資料中提取資訊或者某種模式，從而實現對新的資料也能具有一定的預測作用，這就需要我們找到一個能表示這組資料集合 $D$ 的函式表示式。這樣我們就從離散的點得到了連續的函式曲線，從而可以預測未曾見過的輸入變數。 ​ 一種常見的假設是，將輸入變數和輸出變數之間的關係假設為線性關係：$$h_\theta(\mathbf x) = \theta_0 + \theta_1x_1 + ... + \theta_kx_d= \mathbf{\theta x^T}$$ 。其中 $h$ 為 hypothesis，是我們假設的能夠表示資料集合 $D$ 的假設函式。而我們同時假設，存在一個 true function $f$ ，使得樣本集合 $D$ 中的樣本都是由該函式，加上一定的噪聲產生的（因為我們無法考慮到與響應變數 $y$ 相關的所有的情況，也無法蒐集到所有的資料）。並且很常見的，我們假設噪聲服從正態分佈。機器學習的任務就是從假設函式空間 $H=\{h_1,h_2,...,h_k\}$ 中找到一個對 true function 最好的近似。 ​ 這個尋找 $h$ 的過程，就是機器去學習的過程。 從直觀角度出發，我們可以設定這樣一個目標函式：希望有一條直線能夠距離每個樣本點的距離都十分的近，整體來看，希望距離所有樣本的距離和最近，這樣的一條直線是最有可能接近 true function 的。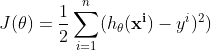形式化表達，可以表示為：  也可稱之為**損失函式**。當該函式取得最小值時，說明當前的這個 $h_\theta$ 是在當前資料集下對 true function 的最好的一個估計。 ​ 所以問題轉化為一個最優化問題，在損失函式最小的情況下的 $\mathbf{\theta}$ 是要求解的。這裡我先舉一個直觀的例子。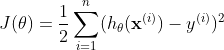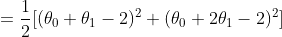假設樣本集合 $D = {(1,2),(2,2)}$，$h_\theta(\mathbf x) = \theta_0 + \theta_1x$ ；在此資料集下求解引數 $\mathbf{\theta}$ ，將資料帶入損失函式：   ​ 以上討論，是希望能直觀化的闡明一點，當帶入所有的資料樣本後，損失函式變成了一個只和引數 $\theta$ 相關的函式。而對於這個二元函式求極值，我相信大家都不會陌生。可以令各個變數的偏導同時為 0 來求解可能的極值點，然後在這些極值點中，尋找最小的點，即為損失函式最小值點，此時對應的 $\theta_0,\theta_1$ 就是我們要求解的引數。帶回假設函式後，該函式就是我們對 true function 的一個近似。而預測過程就很簡單了，只要將新的輸入變數 $x$ 帶入 $h_\theta$ 即可得到響應變數 $y$。 ## 梯度下降演算法 ​ 闡述完背景，接下來討論梯度下降演算法。你應該注意到了，之前對引數 $\theta_0,\theta_1$ 的求解，我們是通過手動計算的方式計算出來的。事實上這個過程應當由計算機來完成，這很自然。那麼一種顯而易見的方法是對手算過程用計算機模擬，即求同時使得損失函式各個偏導都為 0 的點，然後去確定所有的極小值、極大值點，然後得到最小值點。但是呢，這個計算過程，對於人去手算可能並不困難，但是對於計算機求解卻並不容易，因為這涉及到公式的推導，有時情況會很複雜，並且當損失函式形式變得複雜時，這也是不現實的。所以，一種非常簡單而又直覺化的方法被提出——梯度下降演算法。 ​ 梯度下降演算法的直觀解釋是，在當前損失函式的某個點上，如果想要到達該函式的最低點，那麼應該向下降速度最快的那個方向走一步，而這個方向，就是梯度的方向。步長採用對該方向分量的偏導值，也就是梯度的值。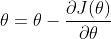梯度下降演算法的引數 $\theta$ 更新公式為：  這裡給出該公式的一個直觀解釋，以及它為什麼可行。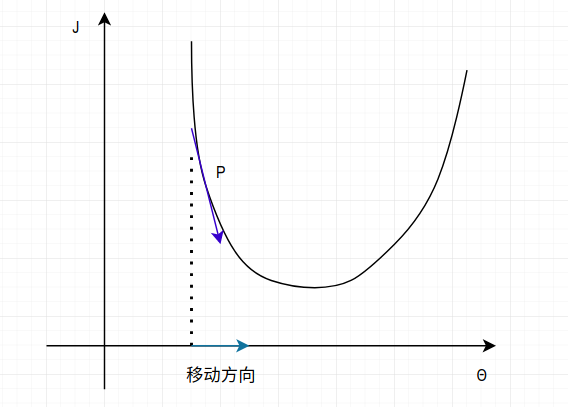參考下圖：  ​ 現在只考慮某個分量$\theta_i$ 與函式 $J$ 的關係。當初始化一個 $\theta_i$ 為某個值，它將位於損失函式的某個點 P 上，然後在該點計算一個偏導：$\frac{\partial J(\theta))}{\partial \theta_i}$ ，對應上圖中的深藍色箭頭，此時該偏導為負，所以按照 $\theta$ 的更新公式：$\theta_j = \theta_j - \frac{\partial J(\theta))}{\partial \theta_j}$ 可知 $\theta $ 將向座標軸右方向移動，即更靠近函式的最低點。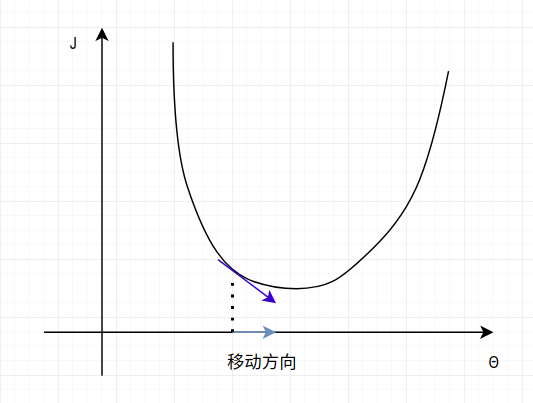  ​ 當進行了數次的迭代更新後，$\theta$ 將不斷向損失函式的最低點靠近，而該點，正是 $\frac{\partial J(\theta))}{\partial \theta_j} = 0$ 的點。此時 $\theta$ 將會收斂。你會發現，這與我們手算偏導為 0 的點是相同的！而這個過程會在每個 $\theta$ 的分量 $\theta_j$ 上進行（相當於我們手算對所有的變元求偏導為 0）。結果如下圖：  此時便完成了對 $\theta$ 的一個分量 $\theta_j$ 的引數搜尋。當偏導為正時，情況類似。 ​ 和我們去手算損失函式的最小值不同，梯度下降演算法去搜索最小點很容易陷入到區域性的極小值中，最後收斂在這一點反而不能找到全域性的最小值。解決這一問題的方法有很多，最常見的就是通過初始化不同的起點，以避免陷入區域性極小值。另一種方法是通過合理調整學習率，通過使演算法每步的步長大一些，從而跳過一些區域性的“凹陷”極小值處（但是過大的學習率也會帶來問題，稍後我將展示這一點）。其實大多數，我們的目標函式都是單一凹凸性的，所以梯度下降演算法一般可以工作的很好。 ### 隨機梯度下降和批梯度下降 ​ 為了得到梯度下降的具體公式，便於用計算機迭代求解，我們需要先做一些推導。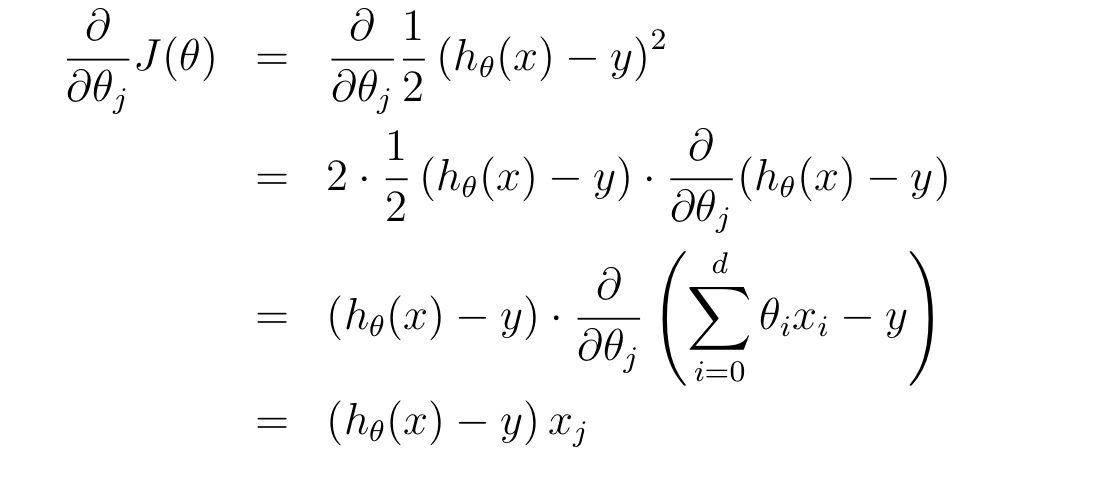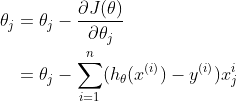我們已知損失函式：$$J(\theta) = \frac{1}{2} \sum_{i=1}^{n} (h_\theta(\mathbf x^{(i)}) - y^{(i)})^2$$ ，假設只有一個樣本時（對於所有樣本的情況，公式幾乎相同，只差一個求和符號），對某個 $\theta$ 分量 $\theta_j$ 求偏導：  所以 $\theta_j $ 的更新公式為（全部樣本集下）：  ​ 我們能發現，這個更新公式的形式很容易用計算機進行模擬。 ​ 對於梯度下降演算法的實現有很多變種，最常見的兩種策略就是**隨機梯度下降**和**批梯度下降**。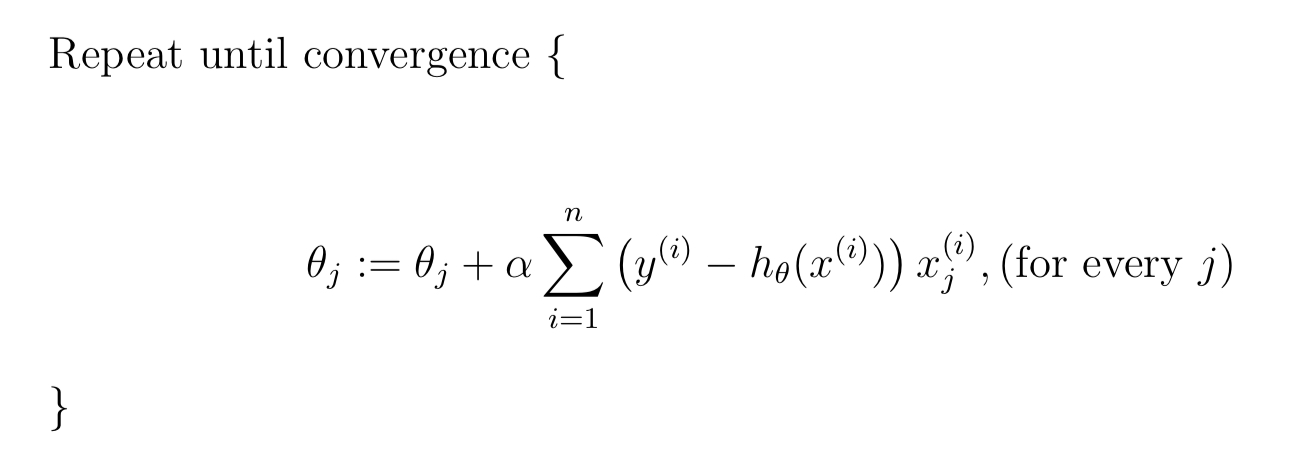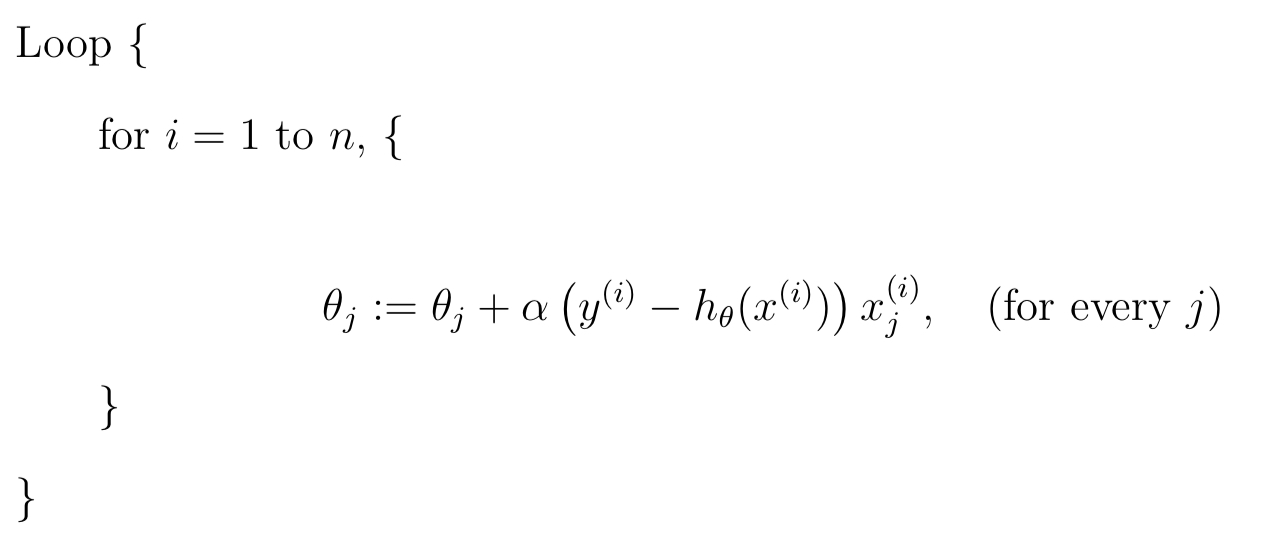 ​ 批梯度下降的虛擬碼為：  ​ 隨機梯度下降的虛擬碼為：  ​ 其中 $\alpha$ 為學習率，控制每次移動的步長。 ​ 批梯度下降的優點是精確，損失函式的每個分量每次更新都會遍歷所有的樣本，計算偏導並進行一次更新，缺點是這樣每次計算量很大。隨機梯度下降每次使用一個樣本進行引數的更新，優點是速度快且有隨機性，缺點是每次只利用了一個樣本。 ​ 對於二者之間折中的方法是**隨機小批量梯度下降演算法**。 ## 隨機小批量梯度下降演算法的實現 ### 問題背景 ​ 首先，假設問題的背景為預測橘子的售價。 ​ 我們假設橘子的售價和橘子的進價、質量和新鮮程度成線性關係，並且存在一個 true function $f$ 在根據這些 attribute 生成橘子的售價，於是假設 true function為： $f = 1.25 * buyinprice + 0.42 * quality + 0.33 * fresh$ 。 但是現實是我們無法對一個現象進行精準的建模，所以為了更好的近似現實情況，我們給 true function 新增一個噪聲項，來表示無法被模型捕獲的因素，並用這個函式來生成我們的樣本資料。所以該函式為：$f = 1.25 * buyinprice + 0.42 * quality + 0.33 * fresh + noise$ 。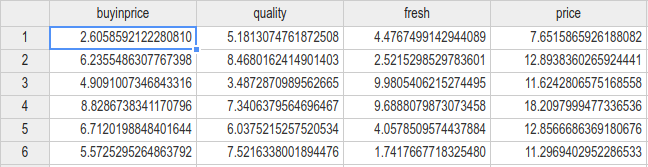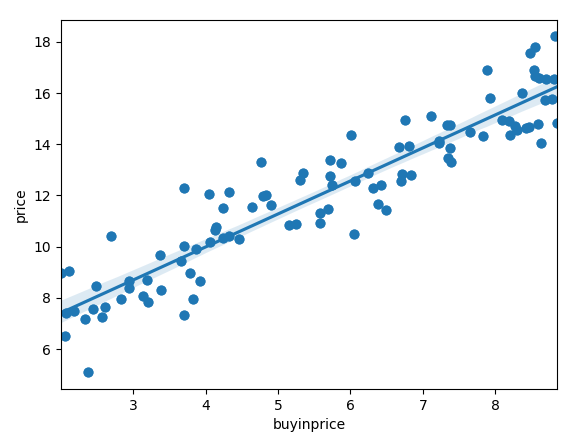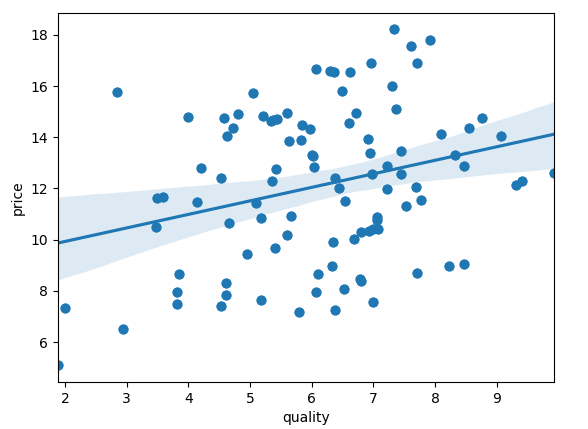 ``` buyinprice = np.random.uniform(2,9,100) quality = np.random.normal(6,1.5,100) fresh = np.random.uniform(1,10,100) noise = np.random.normal(0.85,0.15,100) y = 1.25 * buyinprice + 0.42 * quality + 0.33 * fresh + noise ``` ​ 生成資料如圖（共100組）：  ​ 我們可以先看一下資料 buyinprice 的分佈和與 price 的直觀上的關係： ``` sns.regplot(x='buyinprice',y='price',data=data) ```  ​ quality：  ​ 因為 quality 對 price 的影響遠沒有 buyinprice 大，所以資料顯得比較分散。也就是 quality 與 price 的關係受到另一個維度 buyinprice 的擾動非常大。fresh 與此相似。 接下來考慮進行我們的機器學習程式的設計。 ​ 假設線性迴歸模型：$h_\theta(\mathbf{x}) = \theta_1x_1 + \theta_2x_2 + \theta_3x_3$ 。 ​ 那麼現在我們要從資料集中去學習引數，從而得到我們假設的模型的表示式。 ​ 現在使用隨機小批量梯度下降演算法來進行引數搜尋。 ``` theta = [0.1,0.1,0.1] # initialize theta last_theta = [-100000,-100000,-100000] alpha = 0.001 # learning rate while measure_close(theta,last_theta): random_pick = np.random.uniform(1,100,30) # a small batch sample last_theta = theta[:] # reserve and copy for j in range(3): # update every Θj theta[j] = theta[j] - alpha * par_der(random_pick,last_theta,j) print(theta) ``` ​ 可以看到 theta 的搜尋過程：  ​ 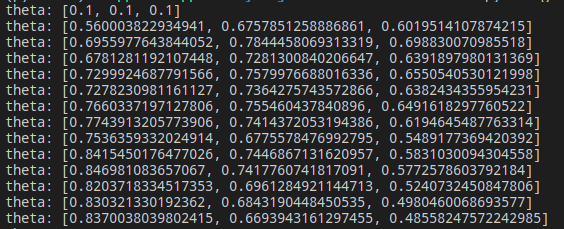經過數輪迭代後：  ​ 最後引數收斂在 $\theta_1 = 1.277,\theta_2 = 0.499,\theta_3 = 0.35$，而這與我們的 true function 的引數是較為接近的，可以認為隨機小批量梯度下降演算法取得了效果。 ​ 然後我們觀察 buyinprice 和price 的 true function 影象與我們通過梯度下降演算法擬合出的影象：  ​ 其中藍色直線為 true function ，而紅色直線為我們通過梯度下降演算法擬合出的直線，可以看到二者十分的接近。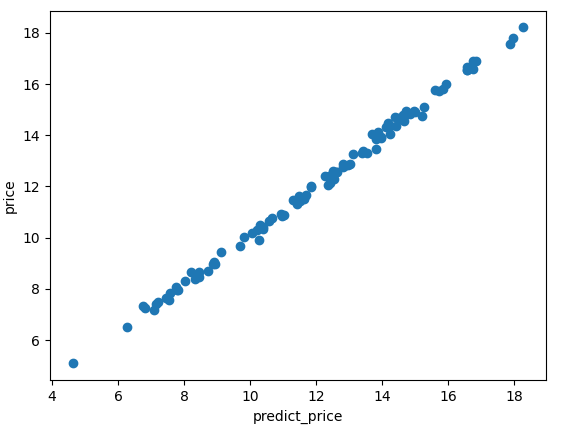 而在整個資料集上，考慮到 quality 和 fresh 因素，得到的模型對 price 的預測 predict_price 和實際的價格 price 之間關係：  ​ 能看到，二者幾乎相等。所以可以認為在訓練資料集上，我們的模型表現的非常好。 ## 超引數調整 ​ 在編寫梯度下降演算法進行引數搜尋時，出現了一個很有意思的 bug。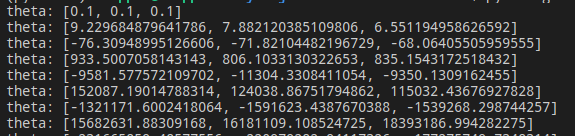剛開始很多次，我的引數搜尋結果都是這樣的：  $\theta$ 變得越來越大，而且速度非常快，很快，我得到了這個結果：  ​ 它的值已經超出了資料範圍。為什麼會出現這個問題？我困擾了很久。直到到想起了超引數（hyper-parameters）。 ​ 我這裡有兩個超引數：learning rate = 0.05，measure close = 0.1。第一個控制步長，第二個控制收斂條件。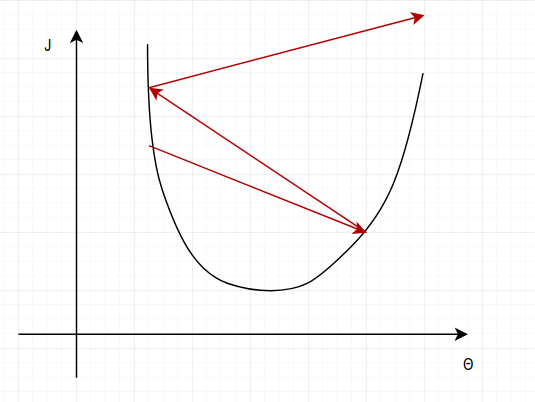measure_close 函式的程式碼如下： ``` def measure_close(theta,last_theta): res = 0 for i in range(3): res += abs(theta[i] - last_theta[i]) if(res >= 0.1): # hyper parameters：0.1 return True else: return False ``` ​ 我想一幅圖可以很好的說明我遇到的問題：  ​ 過大的步長使得梯度下降演算法跳過了最低點，並且 $\theta$ 朝著 x 軸的兩側不斷擴張，最後趨向於無窮。 而此時，通過不斷的調節 learning rate，和 measure close 的值，我們也能搜尋到不同的 $\theta$ 結果，直到找到一個我們覺得滿意的引數為止，這就是機器學習中的超引數調整（調參）。 下圖是我將 learning rate 設定為 0.0012 時的到的引數：  合適的超引數將會得到擬合程度更好的模型。（不考慮泛化能力） ## 注 1. 參考資料 CS229 note1 2. markdown 在部落格園始終這麼醜 ：<

作者：Skipper 出處： https://www.cnblogs.com/backwords/p/13701122.html __本部落格中未標明轉載的文章歸作者 Skipper 和部落格園共有，歡迎轉載，但未經作者同意必須保留此段宣告，且在文章頁面明顯位置給出原文連線，否則保留追究法律責任的權利。__