LCA（Least Common Ancestors），即最近公共祖先，是指這樣一個問題：在有根樹中，找出某兩個結點u和v最近的公共祖先（另一種說法，離樹根最遠的公共祖先）。

　　知識需求：1）RMQ的ST演算法   2）尤拉序列

1）RMQ的ST演算法：

2）尤拉序列：

　　所謂尤拉序，就是從根結點出發，按dfs的順序經過每一個結點最後繞回原點的順序，比如下面這個例子，尤拉序就是A-B-D-B-E-G-E-B-A-C-F-H-F-C-A

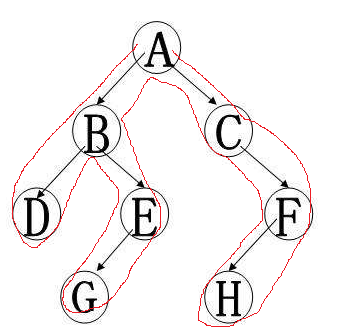
　　那麼尤拉序和rmq與LCA有什麼關係呢，首先我們知道RMQ可以方便的線上求出區間最小值，以求上圖中DG兩點最近公共祖先為例，我們先處理出他的尤拉序，我們記錄下每個結點第一次被訪問的時間，以及每個時間訪問的結點編號與結點深度，這時，我們不難發現，D與G第一次出現的時間之間的區域深度最小值就是這兩個點對應的最近公共祖先B的深度，我們修改rmq，讓其不再返回最小深度，而是返回區間最小深度對應的下標，這裡就是求尤拉序中的訪問時間，有了這個時間，加上之前的記錄，我們可以直接得出該點的編號，從而求出最近公共祖先。

練習題：題目連結

練習題AC程式碼：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <algorithm>
  4 #include <cstring>
  5 #include <vector>
  6 #include <set>
  7 #include <queue>
  8 #include <map>
  9 
 10 using namespace std;
 11 
 12 const
 
 int MAXN = 200010 * 2;
 13 
 14 int rmq[MAXN * 2];    //節點深度序列
 15 
 16 struct ST {
 17     int mm[MAXN * 2];
 18     int dp[MAXN][30];
 19     void init(int n) {
 20         mm[0] = -1;
 21         for(int i = 1; i <= n; ++i) {
 22             mm[i] = ((i & (i - 1)) == 0) ? mm[i - 1] + 1 : mm[i - 1
 
];
 23             dp[i][0] = i;
 24         }
 25         for(int j = 1; j <= mm[n]; ++j) 
 26             for(int i = 1; i + (1 << j) - 1 <= n; ++i) 
 27                 dp[i][j] = rmq[dp[i][j - 1]] < rmq[dp[i + (1 << (j - 1))][j - 1]] ? dp[i][j - 1] : dp[i + (1 << (j - 1))][j - 1];
 28     }
 29 
 30     int query(int a, int b) {
 31         if(a > b) swap(a, b);
 32         int k = mm[b - a + 1];
 33         return rmq[dp[a][k]] <= rmq[dp[b - (1 << k) + 1][k]] ? dp[a][k] : dp[b - (1 << k) + 1][k];
 34     }
 35 };
 36 
 37 struct Edge{
 38     int to, next;
 39 };
 40 
 41 Edge edge[MAXN * 2];
 42 int tot, head[MAXN];
 43 
 44 int F[MAXN * 2];
 45 int P[MAXN];
 46 int cnt;
 47 ST st;
 48  
 49 void init() {
 50     tot = 0;
 51     memset(head, -1, sizeof(head));
 52 }
 53 
 54 void addedge(int u, int v) {
 55     edge[tot].to = v;
 56     edge[tot].next = head[u];
 57     head[u] = tot++;
 58 }
 59 
 60 int d[MAXN];
 61 
 62 void dfs(int u, int pre, int dep) {
 63     d[u] = dep;
 64     F[++cnt] = u;
 65     rmq[cnt] = dep;
 66     P[u] = cnt;
 67     for(int i = head[u]; i != -1; i = edge[i].next) {
 68         int v = edge[i].to;
 69         if(v == pre) continue;
 70         dfs(v, u, dep + 1);
 71         F[++cnt] = u;
 72         rmq[cnt] = dep;
 73     }
 74 }
 75 
 76 void LCA_init(int root, int node_num) {
 77     cnt = 0;
 78     dfs(root, root, 0);
 79     st.init(2 * node_num - 1);
 80 }
 81 
 82 int query_lca(int u, int v) {
 83     return F[st.query(P[u], P[v])];
 84 }
 85 
 86 int main()
 87 {
 88     int T, N, u, v;
 89     scanf("%d", &N);
 90     init();
 91     for(int i = 1; i < N; ++i) {
 92         scanf("%d%d", &u, &v);
 93         addedge(u, v);
 94         addedge(v, u);
 95     }
 96     LCA_init(1, N);
 97 
 98     long long ans = 0;
 99     for(int i = 1; i + i <= N; ++i) {
100         for(int j = i + i; j <= N; j += i) {
101             ans += d[i] + d[j] + 1 - 2 * d[query_lca(i, j)];
102         }
103     }
104     printf("%lld\n", ans);
105     
106     return 0;
107 }