上週寫完了《《三體》讀後思考-泰勒展開/維度打擊/黑暗森林》後收到一些郵件，進一步思考了關於泰勒展開的意義。也許我掌握的那些網路技術比如Linux Netfilter，NAT之類，太過底層太過小眾，所以大家幾乎都是沒有感興趣的，倒是這種科普性質的文章和那些吐槽類的文章，會引發一系列的互動，這對我來講是好事，因為我喜歡跟人交流技術和思想。

宣告

本來這篇文章應該新增在《三體》讀後感後的“補遺”一節呢，後來覺得太長了，有點喧賓奪主的意思，就單獨寫了一篇文章。   其實吧，這篇文章已經跟《三體》小說沒有太大的關係了，這純粹是一篇關於數學的文章，但是由於本文要涉及大量關於“趨勢的趨勢的趨勢”，“走勢的走勢的走勢的走勢”，“導數的導數的導數的導數的導數…”，為了保持一致性，我將本文的題目寫成了“《三體》讀後感的讀後感…”，可能後面還有，未完待續！

第一部分.泰勒展開解釋

很多人對我解釋的泰勒展開提出了自己的疑問，這些疑問大致都是對下面的問題表示不解： 為什麼可以從一個單獨的點不斷求導就可以畫出整個函式的曲線？即“一點是如何蘊含整個世界”的。 誠然，這個問題其實在數學上是及其容易證明的，在定量的角度，隨便找出一本講微積分或者數學分析的書都可以得到令人滿意的回答，我在文章《《三體》讀後思考-泰勒展開/維度打擊/黑暗森林》中也給出了一個簡易的推導。然而，在滿足了邏輯上的自洽後，我們很多人對一件邏輯上合情合理的事情便有了探索其實際意義的慾望，比如我們會問，它的物理意義是什麼，它的幾何意義是什麼，甚至更基本的，它的意義是什麼？就這麼問著問著，便似乎有了一點哲學探索的味道，在我看來，這便是最精彩的！     很多人都看過雙截棍表演，但現如今很少有人瞭解鞭術了，其實你可以把鞭子看成是N趨近於無窮大時的N截棍，玩起來更難。其實我也不是很懂，就是為了解釋這個泰勒展開才稍微看了一點關於鞭術的東西，具體來講，執鞭人手執鞭子在原地只是上下左右按照一定的規則甩鞭，一條很長的鞭子就會整體展現成各種漂亮的曲線，他是怎麼做到的？     當然，從物理上講，這當然是若干列波從執鞭處向鞭子的另一端傳播，傳播的過程在不同的點產生了定向的效果，然而似乎不是一個很好的足以讓人滿意的解釋，我們的問題是，那個執鞭人的手需要怎麼個動作，才能讓鞭子整體上看來是那種效果？   這個問題我是回答不了，因為我不懂鞭術，身邊也沒有懂的人，但是這個問題似乎和本文一開始的那個問題講的是同一回事，即從一個點來蘊含整體的行為。 …   我的觀點是：既然走勢可以讓人預測曲線上鄰接的下一點的大致位置，那麼走勢的走勢便可以相對精確地預測鄰接下一點的具體位置，緊接著，走勢的走勢的走勢便可以告訴人們這種趨勢可以延續到什麼時候，再繼續…

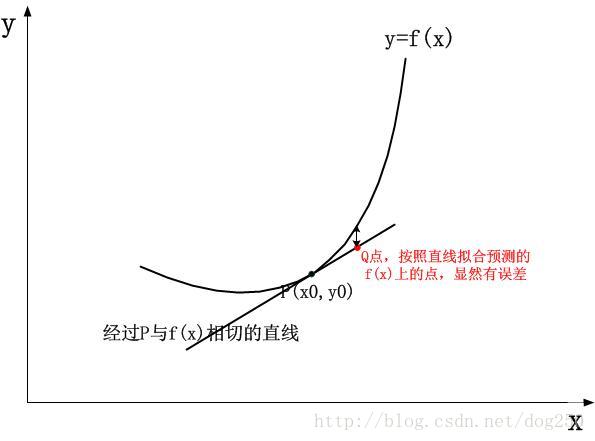
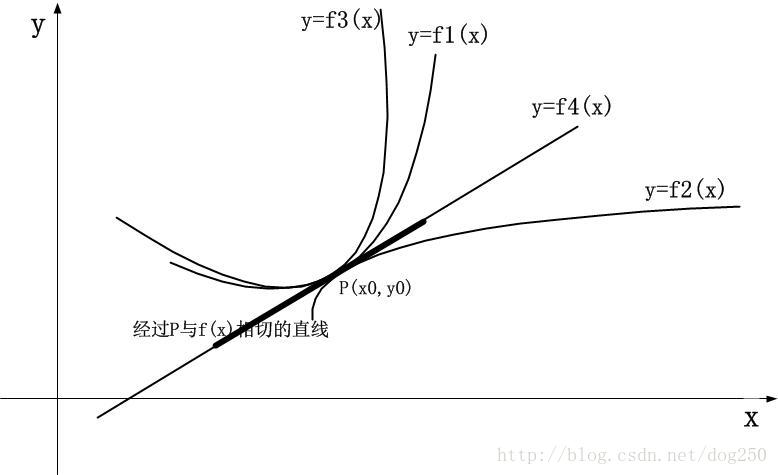
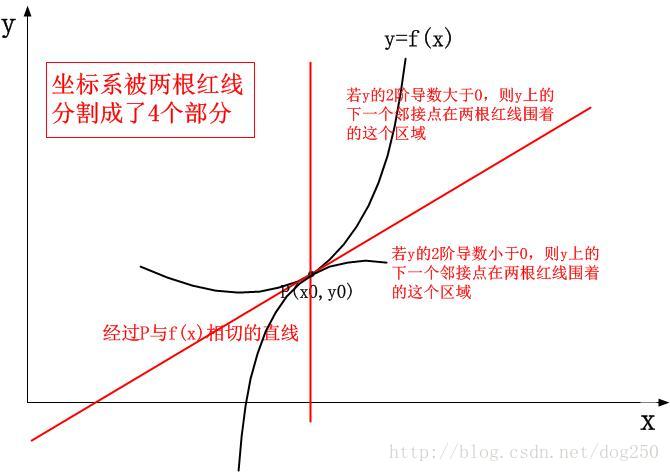
我們來看這個1階導數可以預測到多遠處呢？如果我們僅僅知道該點的座標以及有這麼一個該點的1階導數的值，我們幾乎什麼都預測不了，除了知道在該點處有沿著切線向上的趨勢之外，這沒能為我們畫出這個曲線帶來幫助，似乎下面的曲線都能滿足，然而真正正確的只有一個：

換句話說，1階導數只能將鄰接的下面的點定位到兩個範圍中的一個：

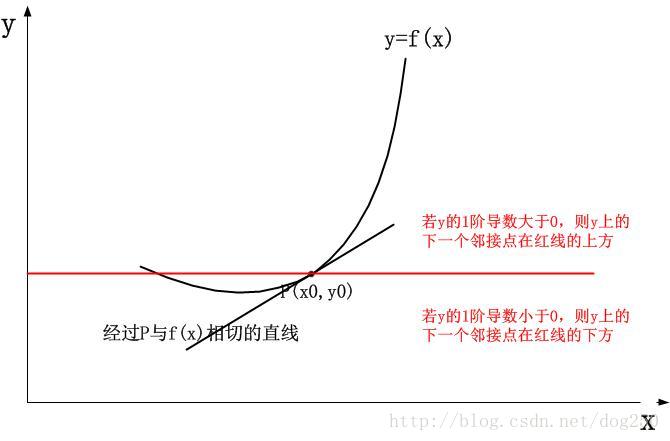
so，我們需要進一步的資訊，我們繼續求2階導數，看看能挖掘出什麼新玩意兒。   2階導數是1階導數的導數，換句話說，它代表了檢測點切線的變化趨勢，有了這個趨勢，我們是不是可以相對精確地預測鄰接的點的位置了呢？我們先看2階導數的幾何意義為何。學過數學的都知道，2階導數表示了曲線的凸凹，對於凸函式，2階導數是負數，它表示切線的斜率會越來越小，而對於凹函式，2階導數是正數，它表示切線的斜率越來越大：

因此，有了2階導數，我們對接下來的曲線走勢定位就更加精確了，我們可以進一步縮小鄰接的點的取值範圍：

具體的座標由2階導數的具體值來約束。   到了這一步，進一步將曲線往前延伸似乎是無望的，因為：

 

1.首先，我們不知道代表檢測點凸凹性的2階導數的值在將來會不會逆轉，即我們不知道曲線會不會由凸變凹或者由凹變凸；   2.其次，即便假設函式的凸凹性不變，我們也不知道接下來曲線是越來越凸/凹呢？還是反過來呢？

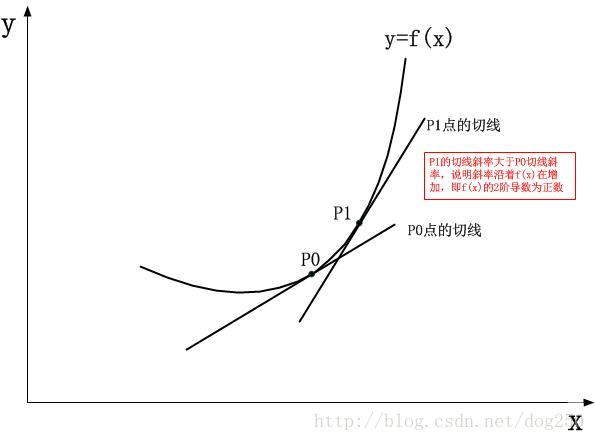
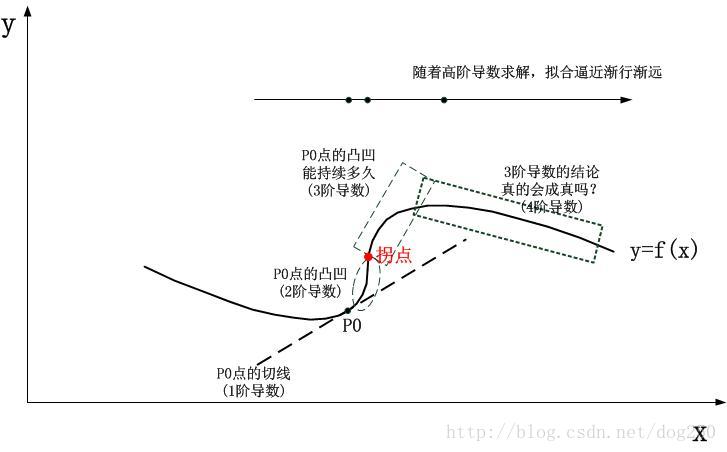
畢竟，我們只求得了檢測點的1階和2階導數，注意，它們都只是一個數字，而不是一個帶有自變數的新的函式，所以我們通過1階導數和2階導數，得到僅僅是2個值，僅此而已，如果我們能得到關於曲線任意一點的2階導數的函式表示式，那麼我們當然可以預測曲線2階函式的走勢，但在本文中，我不會那麼做，我就假設，我們沒有這個函式表示式，只有一個檢測點的2階導數的值！怎麼辦？   我們繼續看3階導數。在此之前，我必須要澄清一個我的觀點。   我在知乎上查過相關資料，另外還特意請教過一些搞數學的老師或者朋友，得到的解答可能都是從哪個地方看到的一致性解答，說3階，4階，5階…導數這些沒有幾何意義和物理意義，數學只追求邏輯上的完整，自包容，而不是去追求什麼幾何意義，物理意義。我並不贊成這個說法，以霍金為例，它的虛時間模型雖然只是數學上的技巧，但是最終的目標卻是為他的有限無界的宇宙幾何模型服務，這說明，完成邏輯完整性證明和尋找其意義同等重要，可能後者還會更重要，我沒有看到哪一個偉大的物理學發現背後僅僅是純粹的思辨性的數學，不管是牛頓的引力場，還是愛因斯坦的引力場，還是霍金的量子引力，在邏輯嚴謹性支撐的前臉，都有一個漂亮得體的幾何模型作為表象。 …   3階導數不難求，繼續對2階導數表示式求導，然後代入檢測點的x值即可，然而3階導數的意義是什麼？其實仔細想想，並不難理解，這正如2階導數主導1階導數的變化從而把1階導數自認為正確的“以直代曲”的直線模擬拉成彎曲的或者凸或者凹的曲線一樣，3階導數同樣主導2階導數的變化，它可以表示“曲線是繼續凸下去或者繼續凹下去，還是會在某一個x值後逆轉，由凸變凹或者由凹變凸”。用語言表示比較蒼白難以理解，於是我畫個圖示：

好了，有了3階導數，我們似乎進一步將曲線向前推進了，至少是預測出了一種趨勢，然而這個趨勢是必然的嗎？考慮到一種情況，比如當前檢測點的2階導數值為1，表示曲線在檢測點是凹的，而同時3階導數的值為-1，這表示可能接下來鄰接點的2階導數會比1小一點，最終會變成0甚至負數，這意味著曲線會由凹變凸，即經歷一個拐點，但這種預測一定會發生嗎？   不一定！But why？   雖然當前檢測點的3階導數值為-1，但這並不意味著它會一直保持-1，如果它一直保持-1，那麼我們的預測正確，但是如果曲線的3階導數在該檢測點是遞增的呢？這意味著會發生下面的情況： 在曲線從檢測點x0這些函式的奇點在哪裡？這些函式的奇點在無窮遠處。這意味著，在任意一個展開點，函式曲線本身都已經積累的無窮的能量(即資訊)，這說明泰勒公式可以將其完全展開到無窮。   離奇點越近，各種趨勢越不易表現出來，奇點附近剛開始積累趨勢，趨勢尚未表現，這就是能量和運動的觀點，我就是這樣避開了那些收斂圓，收斂半徑這些概念的。

C.到底什麼是數學

如果你覺得數學純思辨性的類似哲學的東西，那麼你可以忽略我下面的所述，如果不是，請看完它，哪怕是心裡壓著邪火，保持著憤怒。   只有在古希臘數學才是純思辨哲學的分支，從羅馬帝國的地中海世界開始，一直到今天，數學都只是工具，解題工具。當然這裡說的解題並非我們考試中的解題，而是實實在在的處理資料時必須要解決的難題。   不要把煉丹術和占星術看作是迷信這種不可救藥的東西，它們和數學的關係源遠流長。首先指出，現代數學和古希臘數學完全不是一個概念，甚至幾乎沒有什麼關聯，所以在理解現代數學本質的概念的時候，千萬不要去想什麼畢達哥拉斯學派什麼的。煉丹術和占星術是現代化學和天文學的先祖，當它們無法用咒語欺騙國王的時候，它們就必須拿出證據來保住自己的飯碗，這無形中將它們推向了現代科學的“深淵”。千萬不要將哥白尼，伽利略，牛頓…他們看成是擁有現代科學品質的明事理的人，在他們的年代，他們無一例外都披著神學的外衣，只是他們在處理一些棘手問題的時候，偶然間發現了一些所謂的真相，要讓這些真相在邏輯上變得合理，他們必須處理大量的資料從而期望匯出一些隱藏在這些資料背後的關係。在處理資料的時候，他們無一例外地被資料和關係的複雜性困擾，於是乎他們搞出一些處理技巧，這些技巧就是現代數學的前身，因此可以說煉丹術和占星術引導了現代物理，現代物理激發了現代數學，這其中一脈相承的就是神學和哲學的不斷滲透和對抗。   明白了這些之後，你會發現現在中學大學裡的數學課程的教法是多麼沒有意義。這些課程看似很深邃，然而都是毫無意義的。我記得我上大學的時候(當時還是本科，後來才“進修到大專”)，老師給我們講梯度散度旋度，最後的輸出就是背誦了一大堆的定理和公式，我問老師這些有什麼用，老師說這些期末考試是必考點，以後考研也會考…後來我退學後跑到了女朋友(小小的媽媽)學校外面的村子裡租了個房子，剛過去時，正逢她們班要期末考試了，也要考高等數學，什麼洛必達法則，牛頓/萊布尼茲公式…爆炸，她們是日語教育專業啊！考這玩意兒毛用啊！   然而抱怨是蒼白的，我依然要拖著疲憊的身軀去給她們講高等數學，對了，還包括她的同班男生，反正就是我女朋友全班…講著講著我就上癮了(其實也沒講多久)，當有人問我學這些有什麼用的時候，我總是微笑著回答，這些都是必考點，以後你們考研也會考，說這話時我特別自豪，微笑裡帶著些許嘲諷和灑脫，因為我TMD再也不用考試和考研了！我不知道當時這樣回答我的老師是不是也是這麼想的。 …. 在以後的學習生涯中，我徹底摒棄了學校裡的那一套，因為我再也不用考試了，而且也不會再參加任何形式的考試。所以我變得天馬行空，我從馬鞍面匯出了Linux Netfilter的設計模型，最終確認作者也是這麼想的，然後我想僅僅是精通iptables的配置或者看完conntrack的程式碼是多麼Low啊，於是便更進一步探索了Cisco和Netfilter在設計上的差異，最終實現了基於Netfilter的Cisco模型…在我學習最小二乘法的時候，我試圖理解平方的深意，後來我看了牛頓的《原理》之後，發現了平方律和立方律簡直就是構成我們世界的基本元素啊！   王姐姐說牛頓是外星人，我表示贊同。然而牛頓是怎麼思考的？！   1905年，愛因斯坦的奇蹟年，主角是一位不修邊幅，收入不高的專利局小職員，有點像《三體》小說作者劉慈欣，在火電站工作，不好好上班天天上班時間寫小說…然而就是這個愛因斯坦道出了現代數學的本質，它只是工具！愛因斯坦從來沒有系統學習過現代數學，他只是在用到的時候去請教身邊的數學專家，他真的就是把數學當扳手使的。我不曉得其它的人怎麼想，我只知道，狄拉克的算符，費曼的積分，霍金的虛時間軸，這些都是數學上的技巧，你要是問有什麼物理意義，我覺得他們本人都說不出，只是這麼處理很方便，僅此而已吧。   那麼，既然現代數學只是個工具，豈不是很Low？！No！每一個數學上的突破，均代表了一系列的總結，最終會引領新的突破，這方面，數學已經替代了哲學。在我工作的計算機領域，任何一個想法，如果你不能用數學表示出來，那便是不可處理的，請問不可處理的東西能完成KPI嗎？於是便有了數學建模。然而模型的建立談何容易。 【外出買菜，未完待續】 (TODO)