OpenCascade中的Delaunay三角剖分
Delaunay Triangulation in OpenCascade
摘要:本文簡要介紹了Delaunay三角剖分的基礎理論,並使用OpenCascade的三角剖分演算法將邊界BRep表示的幾何體進行三角離散化後在OpenSceneGraph中顯示。
關鍵字:Delaunay Triangulation、OpenCascade、OpenSceneGraph
一、 概述
三角剖分是平面剖分中的一個重要課題,在數字影象處理、計算機三維曲面造型、有限元計算、逆向工程等領域有著廣泛應用。由於三角形是平面域中的單純形,與其他平面圖形相比,其有描述方便、處理簡單等特性,很適合於對複雜區域進行簡化處理。因此,無論在計算幾何、計算機圖形處理、模式識別、曲面逼近,還有有限元網格生成方面有廣泛的應用。
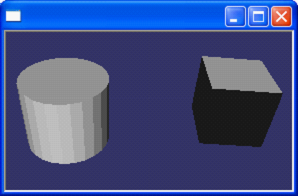
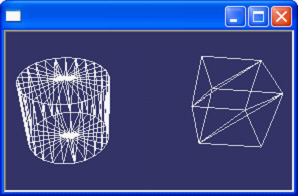
雖然曲線、曲面等有精確的方程來表示,但是在在計算機中,只能用離散的方式來逼近。如曲線可用直線段來逼近,而曲面可用多邊形或三角形來表示。用多邊形網格表示曲面是設計中經常使用的形式,可以根據應用要求選擇網格的密度。利用三角形面片表示的曲面在計算機圖形學中也稱為三角形網格。用三角形網格表示曲面需要解決幾個問題:三角形的產生、描述、遍歷、簡化和壓縮等,這些問題都是計算幾何研究的範疇,相關問題都可以從中找到答案。下圖所示的圓柱和立方體是由OpenCascade生成,使用OpenCascade的演算法離散成三角網格後在OpenSceneGraph中顯示的效果。
Figure 1.1 Shaded Cylinder and Box
Figure 1.2 Mesh generated by OpenCascade
從圖中可以看出,平面的三角形網格效果還不錯,曲面的三角形網格表示只能是近似表示,可以通過提高網格的密度來增加真實性,但相應渲染的資料量就大了。有人說OpenCascade的顯示模組做得不是很好,上述方法則可以只使用OpenCascade的造型模組,再結合OpenSceneGraph來對圖形進行顯示。
三維資料交換STL格式檔案中儲存的都是三角面片的資料,STL檔案格式是由美國3D System公司開發,已被工業界認為是目前快速自動成型領域的準標準零件描述檔案格式。它對三維實體描述的解釋具有惟一性。幾乎所有的幾何造型系統都提供STL檔案資料交換介面。OpenCascade中的資料交換模組也提供對STL格式的支援,由此可見三角網格在幾何造型系統中的重要性。
Voronoi圖和Delaunay三角剖分的應用領域十分廣泛:幾何建模——用來尋找三維曲面“好的”三角剖分;有限元分析——用來生成“好的”有限元網格;地理資訊系統——用來進行空間領域分析;結晶學——用來確定合金的結構;人類學和考古學——用來確定氏族部落、首領權威、居住中心或堡壘等的影響範圍;天文學——用來確定恆星和星系的分佈;生物學生態學和林學——用來確定動植物的競爭;動物學——分析動物的領地;統計學和資料分析——用來分析統計聚合;機器人學——用來進行運動軌跡規劃(在存在障礙物的情況下);模式識別——作為尋找物體骨架點的工具;生理學——用來分析毛細作用的領域;氣象學——用來估計區域平均降雨量;市場學——用來建立城市的市場輻射範圍;以及在遙感影象處理、化學、地理學、地質學、冶金學、數學等學科的應用等。
本文只對OpenCascade中的三角剖分進行簡要介紹,希望對三角剖分在三維幾何造型方面有興趣的朋友可以對其深入研究。水平很有限,文中不當之處歡迎批評指正、指導,聯絡郵箱:[email protected]。
二、 Voronoi圖
Dirichlet於1850年研究了平面點的鄰域問題,Voronoi於1908年將其結果擴充套件到高維空間。半空間定義Voronoi圖:給定平面上n個點集S,S={p1, p2, …, pn}。定義:
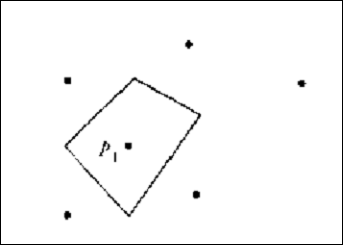
PiPj連線的垂直平分面將空間分為兩半,V(Pi)表示比其他點更接近Pi的點的軌跡是n-1個半平面的交,它是一個不多於n-1條邊的凸多邊形域,稱為關聯於Pi的Voronoi多邊形或關聯於Pi的Voronoi域。如下圖所示為關聯於P1的Voronoi多邊形,它是一個四邊形,而n=6.
Figure 2.1 n=6時的一種V(p1)
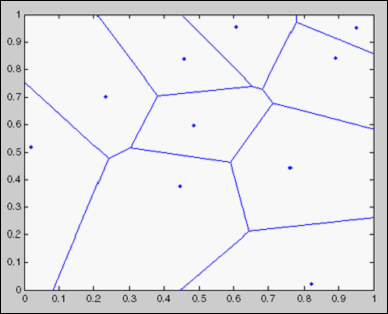
對於點集S中的每個點都可以做一個Voronoi多邊形,這樣的n個Voronoi多邊形組成的圖稱為Voronoi圖,記為Vor(S)。如下圖所示:
Figure 2.2 Voronoi diagram for 10 randomly points (Generated by MATLAB)
圖中的頂點和邊分別稱為Voronoi頂點和Voronoi邊。顯然,|S|=n時,Vor(S)劃分平面成n個多邊形域,每個多邊形域V(Pi)包含S中的一個點而且只包含S中的一個點,Vor(S)的邊是S中某點對的垂直平分線上的一條線段或半直線,從而為該點對所在的兩個多邊形域所共有。Vor(S)中有的多邊形域是無界的。
Figure 2.3 Ten shops in a flat city and their Voronoi cells
(http://en.wikipedia.org/wiki/Voronoi_diagram)
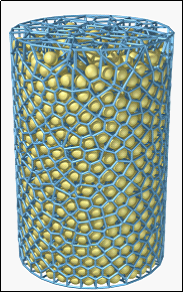
Figure 2.4 Voronoi tessellation in a cylinder (Voro++ library: http://math.lbl.gov/voro++/)
Voronoi圖有如下性質:
l n個點的點集S的Voronoi圖至多有2n-5個頂點和3n-6條邊;
l 每個Voronoi點恰好是三條Voronoi邊的交點;
l 設v是Vor(S)的頂點,則圓C(v)內不含S的其他點;
l 點集S中點Pi的每一個最近鄰近點確定V(Pi)的一條邊;
l Voronoi圖的直線對偶圖是S的一個三角剖分;
l 如果Pi,Pj屬於S,並且通過Pi,Pj有一個不包含S中其他點的圓,那麼線段PiPj是點集S三角剖分的一條邊,反之亦成立。
三、 Delaunay三角剖分
1. 二維實數域上的三角剖分
假設V是二維實數域上的有限點集,邊e是由點集中的點作端點構成的封閉線段,E為e的集合,那麼該點集V的一個三角剖分T=(V,E)是一個平面圖:
l 除了端點,平面圖中的邊不包含點集中的任何點;
l 沒有相交邊;
l 平面圖中所有的面都是三角面,且所有三角面的合集是點集V的凸包。
2. Delaunay邊
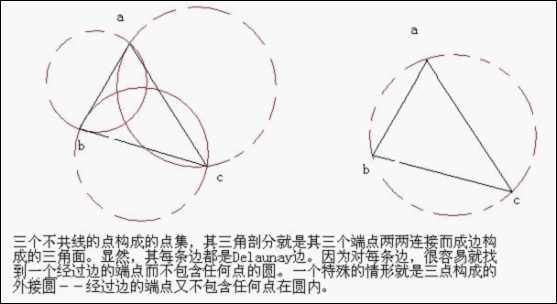
假設E中的一條邊(兩端點a,b),e滿足下列條件,則稱為Delaunay邊:存在一個圓經過a,b兩點,圓內不包含點集V中的任何的點。這一特性又稱為空圓特性。
3. Delaunay三角剖分
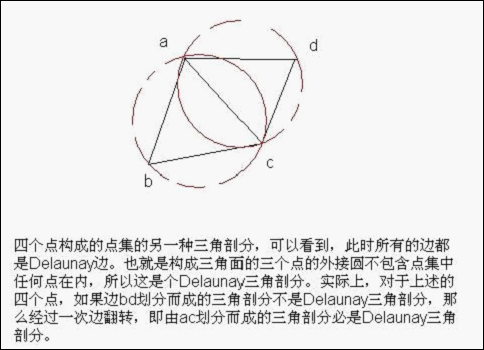
如果點集V的一個三角剖分T中只包含Delaunay邊,那麼該三角剖分稱為Delaunay剖分。
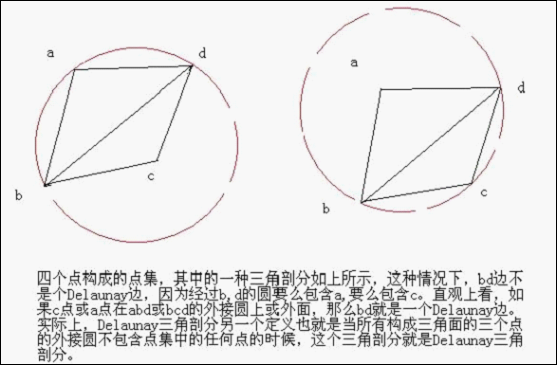
最近點意義下的Voronoi圖的對偶圖實際上是點集的一種三角剖分,該三角剖分就是Delaunay剖分(表示為DT(S)),其中每個三角形的外接圓不包含點集中的其他任何點。因此,在構造點集的Voronoi圖之後,再作其對偶圖,即對每條Voronoi邊作通過點集中某兩點的垂直平分線,即得到Delaunay三角剖分。
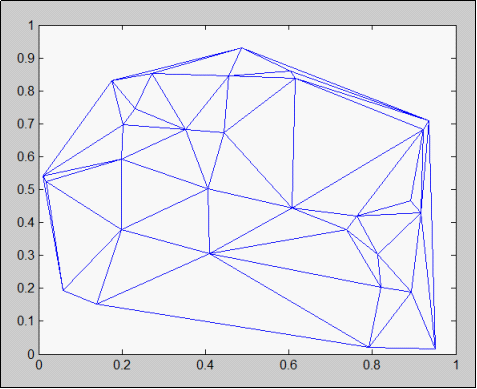
Figure 3.1 Delaunay Triangulation (Generated by MATLAB)
再看幾個圖片,加深對Delaunay三角剖分的理解:
Figure 3.2 Delaunay Edge
Figure 3.3 Illustrate Delaunay Edge
Figure 3.4 Delaunay Edge
4. Delaunay三角剖分的特性
l 1978年Sibson證明了在二維的情況下,在點集的所有三角剖分中,Delaunay三角剖分使得生成的三角形的最小角達到最大(max-min angle)。因為這一特性,對於給定點集的Delaunay三角剖分總是儘可能避免“瘦長”三角形,自動向等邊三角形逼近;
l 區域性優化與整體優化(locally optimal and globally optimal);
l Delaunay空洞(cavity)與區域性重連(local reconnection);
5. 經典的Delaunay三角剖分演算法
目前常用的演算法分為幾種,有掃描線法(Sweepline)、隨機增量法(Incremental)、分治法(Divide and Conquer)等。
經典的Delaunay三角剖分演算法主要有兩類:Bowyer/Watson演算法和區域性變換法。
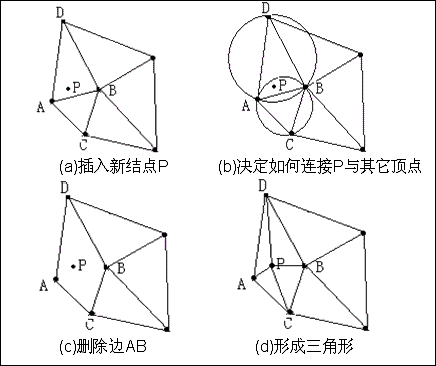
l Bowyer/Watson演算法又稱為Delaunay空洞演算法或加點法,以Bowyer和Watson演算法為代表。從一個三角形開始,每次加一個點,保證每一步得到的當前三角形是區域性優化的。以英國Bath大學數學分校Bowyer,Green,Sibson為代表的計算Dirichlet圖的方法屬於加點法,是較早成名的演算法之一;以澳大利亞悉尼大學地學系Watson為代表的空外接球法也屬於加點法。加點法演算法簡明,是目前應用最多的演算法,該方法利用了Delaunay空洞性質。Bowyer/Watson演算法的優點是與空間的維數無關,並且演算法在實現上比區域性變換演算法簡單。該演算法在新點加入到Delaunay網格時,部分外接球包含新點的三角形單元不再符合Delaunay屬性,則這些三角形單元被刪除,形成Delaunay空洞,然後演算法將新點與組成空洞的每一個頂點相連生成一個新邊,根據空球屬性可以證明這些新邊都是區域性Delaunay的,因此新生成的三角網格仍是Delaunay的。
Figure 3.5 Illustration of 2D Bowyer/Watson algorithm for Delaunay Triangulation
l 區域性變換法又稱為換邊、換面法。當利用區域性變換法實現增量式點集的Delaunay三角剖分時,首先定位新加入點所在的三角形,然後在網格中加入三個新的連線該三角形頂點與新頂點的邊,若該新點位於某條邊上,則該邊被刪除,四條連線該新點的邊被加入。最後,在通過換邊方法對該新點的區域性區域內的邊進行檢測和變換,重新維護網格的Delaunay性質。區域性變換法的另一個優點是其可以對已存在的三角網格進行優化,使其變換成為Delaunay三角網格,該方法的缺點則是當演算法擴充套件到高維空間時變得較為複雜。
四、 Delaunay三角剖分在OpenCascade的應用
OpenCascade中網格剖分的包主要有BRepMesh、MeshAlgo、MeshVS,其中,類MeshAlgo_Delaunay使用演算法Watson來進行Delaunay三角剖分。從類StlTransfer中的註釋The triangulation is computed with the Delaunay algorithm implemented in package BRepMesh.可以看出包BRepMesh就是Delaunay三角剖分的具體實現。使用方法如下:
BRepMesh::Mesh (aShape, Deflection);
這個函式主要是用來對拓撲形狀進行三角剖分。以下通過將一個圓柱三角剖分為例說明如何將一個拓撲形狀進行三角剖分並將結果進行視覺化。
 /**
/** 
 * Copyright (c) 2013 eryar All Rights Reserved.
* Copyright (c) 2013 eryar All Rights Reserved. 
 *
* 
 * File : Main.cpp
* File : Main.cpp 
 * Author : [email protected]
* Author : [email protected] 
 * Date : 2013-05-26
* Date : 2013-05-26 
 * Version : 0.1
* Version : 0.1 
 *
* 
 * Description : Use BRepMesh_Delaun class to learn
* Description : Use BRepMesh_Delaun class to learn 
 * Delaunay's triangulation algorithm.
* Delaunay's triangulation algorithm. 
 *
* 
 */
*/ 
 // Open Cascade library.
// Open Cascade library. 
 #include <gp_Pnt.hxx>
#include <gp_Pnt.hxx> 
 #include <gp_Pln.hxx>
#include <gp_Pln.hxx> 
 #include <BRep_Tool.hxx>
#include <BRep_Tool.hxx> 
 #include <TopoDS.hxx>
#include <TopoDS.hxx> 
 #include <TopoDS_Edge.hxx>
#include <TopoDS_Edge.hxx> 
 #include <TopoDS_Wire.hxx>
#include <TopoDS_Wire.hxx> 
 #include <TopoDS_Face.hxx>
#include <TopoDS_Face.hxx> 
 #include <BRepBuilderAPI_MakeEdge.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx> 
 #include <BRepBuilderAPI_MakeWire.hxx>
#include <BRepBuilderAPI_MakeWire.hxx> 
 #include <BRepBuilderAPI_MakeFace.hxx>
#include <BRepBuilderAPI_MakeFace.hxx> 
 #include <BRepPrimAPI_MakeBox.hxx>
#include <BRepPrimAPI_MakeBox.hxx> 
 #include <BRepPrimAPI_MakeCone.hxx>
#include <BRepPrimAPI_MakeCone.hxx> 
 #include <BRepPrimAPI_MakeCylinder.hxx>
#include <BRepPrimAPI_MakeCylinder.hxx> 
 #include <BRepPrimApI_MakeSphere.hxx>
#include <BRepPrimApI_MakeSphere.hxx> 
 #include <BRepMesh.hxx>
#include <BRepMesh.hxx> 
 #include <TopExp_Explorer.hxx>
#include <TopExp_Explorer.hxx> 
 #include <Poly_Triangulation.hxx>
#include <Poly_Triangulation.hxx> 
 #include <TShort_Array1OfShortReal.hxx>
#include <TShort_Array1OfShortReal.hxx> 
 #pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKernel.lib") 
 #pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKMath.lib") 
 #pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKBRep.lib") 
 #pragma comment(lib, "TKPrim.lib")
#pragma comment(lib, "TKPrim.lib") 
 #pragma comment(lib, "TKMesh.lib")
#pragma comment(lib, "TKMesh.lib") 
 #pragma comment(lib, "TKTopAlgo.lib")
#pragma comment(lib, "TKTopAlgo.lib") 
 // OpenSceneGraph library.
// OpenSceneGraph library. 
 #include <osgDB/ReadFile>
#include <osgDB/ReadFile> 
 #include <osgViewer/Viewer>
#include <osgViewer/Viewer> 
 #include <osgViewer/ViewerEventHandlers>
#include <osgViewer/ViewerEventHandlers> 
 #include <osgGA/StateSetManipulator>
#include <osgGA/StateSetManipulator> 
 #pragma comment(lib, "osgd.lib")
#pragma comment(lib, "osgd.lib") 
 #pragma comment(lib, "osgDbd.lib")
#pragma comment(lib, "osgDbd.lib") 
 #pragma comment(lib, "osgGAd.lib")
#pragma comment(lib, "osgGAd.lib") 
 #pragma comment(lib, "osgViewerd.lib")
#pragma comment(lib, "osgViewerd.lib") 
 osg::Node* BuildShapeMesh(const TopoDS_Shape& aShape)
osg::Node* BuildShapeMesh(const TopoDS_Shape& aShape) 
 {
{ 
 osg::ref_ptr<osg::Group> root =new osg::Group();
osg::ref_ptr<osg::Group> root =new osg::Group(); 
 osg::ref_ptr<osg::Geode> geode =new osg::Geode();
osg::ref_ptr<osg::Geode> geode =new osg::Geode(); 
 osg::ref_ptr<osg::Geometry> triGeom =new osg::Geometry();
osg::ref_ptr<osg::Geometry> triGeom =new osg::Geometry(); 
 osg::ref_ptr<osg::Vec3Array> vertices =new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> vertices =new osg::Vec3Array(); 
 osg::ref_ptr<osg::Vec3Array> normals =new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> normals =new osg::Vec3Array(); 
 BRepMesh::Mesh(aShape, 1);
BRepMesh::Mesh(aShape, 1); 
 TopExp_Explorer faceExplorer;
TopExp_Explorer faceExplorer; 
 for (faceExplorer.Init(aShape, TopAbs_FACE); faceExplorer.More(); faceExplorer.Next())
for (faceExplorer.Init(aShape, TopAbs_FACE); faceExplorer.More(); faceExplorer.Next()) 
 {
{ 
 TopLoc_Location loc;
TopLoc_Location loc; 
 TopoDS_Face aFace = TopoDS::Face(faceExplorer.Current());
TopoDS_Face aFace = TopoDS::Face(faceExplorer.Current()); 
 Handle_Poly_Triangulation triFace = BRep_Tool::Triangulation(aFace, loc);
Handle_Poly_Triangulation triFace = BRep_Tool::Triangulation(aFace, loc); 
 Standard_Integer nTriangles = triFace->NbTriangles();
Standard_Integer nTriangles = triFace->NbTriangles(); 
 gp_Pnt vertex1;
gp_Pnt vertex1; 
 gp_Pnt vertex2;
gp_Pnt vertex2; 
 gp_Pnt vertex3;
gp_Pnt vertex3; 
 Standard_Integer nVertexIndex1 =0;
Standard_Integer nVertexIndex1 =0; 
 Standard_Integer nVertexIndex2 =0;
Standard_Integer nVertexIndex2 =0; 
 Standard_Integer nVertexIndex3 =0;
Standard_Integer nVertexIndex3 =0; 
 TColgp_Array1OfPnt nodes(1, triFace->NbNodes());
TColgp_Array1OfPnt nodes(1, triFace->NbNodes()); 
 Poly_Array1OfTriangle triangles(1, triFace->NbTriangles());
Poly_Array1OfTriangle triangles(1, triFace->NbTriangles()); 
 nodes = triFace->Nodes();
nodes = triFace->Nodes(); 
 triangles = triFace->Triangles();
triangles = triFace->Triangles(); 
 for (Standard_Integer i =1; i <= nTriangles; i++)
for (Standard_Integer i =1; i <= nTriangles; i++) 
 {
{ 
 Poly_Triangle aTriangle = triangles.Value(i);
Poly_Triangle aTriangle = triangles.Value(i); 
 aTriangle.Get(nVertexIndex1, nVertexIndex2, nVertexIndex3);
aTriangle.Get(nVertexIndex1, nVertexIndex2, nVertexIndex3); 
 vertex1 = nodes.Value(nVertexIndex1);
vertex1 = nodes.Value(nVertexIndex1); 
 vertex2 = nodes.Value(nVertexIndex2);
vertex2 = nodes.Value(nVertexIndex2); 
 vertex3 = nodes.Value(nVertexIndex3);
vertex3 = nodes.Value(nVertexIndex3); 
 gp_XYZ vector12(vertex2.XYZ() - vertex1.XYZ());
gp_XYZ vector12(vertex2.XYZ() - vertex1.XYZ()); 
 gp_XYZ vector13(vertex3.XYZ() - vertex1.XYZ());
gp_XYZ vector13(vertex3.XYZ() - vertex1.XYZ()); 
 gp_XYZ normal = vector12.Crossed(vector13);
gp_XYZ normal = vector12.Crossed(vector13); 
 Standard_Real rModulus = normal.Modulus();
Standard_Real rModulus = normal.Modulus(); 
 if (rModulus > gp::Resolution())
if (rModulus > gp::Resolution()) 
 {
{ 
 normal.Normalize();
normal.Normalize(); 
 }
} 
 else
else 
 {
{ 
 normal.SetCoord(0., 0., 0.);
normal.SetCoord(0., 0., 0.); 
 }
} 
 vertices->push_back(osg::Vec3(vertex1.X(), vertex1.Y(), vertex1.Z()));
vertices->push_back(osg::Vec3(vertex1.X(), vertex1.Y(), vertex1.Z())); 
 vertices->push_back(osg::Vec3(vertex2.X(), vertex2.Y(), vertex2.Z()));
vertices->push_back(osg::Vec3(vertex2.X(), vertex2.Y(), vertex2.Z())); 
 vertices->push_back(osg::Vec3(vertex3.X(), vertex3.Y(), vertex3.Z()));
vertices->push_back(osg::Vec3(vertex3.X(), vertex3.Y(), vertex3.Z())); 

相關推薦
OpenCascade中的Delaunay三角剖分
Delaunay Triangulation in OpenCascade 摘要:本文簡要介紹了Delaunay三角剖分的基礎理論,並使用OpenCascade的三角剖分演算法將邊界BRep表示的幾何體進行三角離散化後在OpenSceneGraph中顯示。 關鍵字:Delaunay Triangulat
VC+OpenGL實現空間三維Delaunay三角剖分
三維建模和等值面的繪製過程中,需要經常使用三角形網格對資料體進行構面。而三角形的生成基於Delaunay三角剖分的演算法實現的。前段時間一直在考慮資料體的任意剖面切割該怎麼做,但是一直被兩個問題所困擾,一個就是交點問題,然後就是對所求交點進行繪製問題(三角形網格面構造)。終於在半個月後有
Delaunay 三角剖分2D(原理 + 原始碼)
Delaunay 三角剖分 程式碼實現< C++版本 > 程式碼框架 定義點類 vector2.h 定義邊類 edge.h 定義三角形類 triangle.h 定義三角剖分類 delaunay.h 定義比較類(用於三角退
cv2 實現Delaunay三角剖分和Voronoi圖(Delaunay Triangulation and Voronoi Diagram)
本文主要介紹使用cv2模組實現Delaunay三角剖分和Voronoi圖。 測試圖片: 示例程式碼: # 匯入模組 import cv2 import numpy as np import random # 檢查點是否在長方形區域內 def rect_contains(rec
OpenCV的Delaunay三角剖分和Voronoi圖的實現
給定平面中的一組點,三角測量指的是將平面細分為三角形,將點作為頂點。在圖1中,我們在左影象上看到一組界標,以及在中間影象中的三角測量。一組點可以有許多可能的三角剖分,但Delaunay三角剖分出眾,因為它有一些不錯的屬性。在Delaunay三角剖分中,選擇三角形使得沒有點在任何三角形的外接圓內。圖2示出了4點
Captain Dialog 2009-09-18 VC+OpenGL實現空間三維Delaunay三角剖分
Captain Dialog 2009-09-18 三維建模和等值面的繪製過程中,需要經常使用三角形網格對資料體進行構面。而三角形的生成基於Delaunay三角剖分的演算法實現的。前段時間一直在考慮資料體的任意剖面切割該怎麼做,但是一直被兩個問題所困擾,一個就是交點
opencv平面三角剖分Delaunay
opencv使用: Subdiv2D 實現三角剖分。 使用參考:https://blog.csdn.net/czl389/article/details/62264960?fps=1&locationNum=5 關於三角剖分的基本知識參考:
8.osg中使用Tesselator分格化(三角剖分)
在球的基礎上進行操作。 效果為與主視窗和子視窗新增一個邊框 osg::ref_ptr<osg::Vec3Array>vertice2 = new osg::Vec3Array(8); //外邊界逆針 (*verti
最優三角剖分
return min std esp div 技術分享 include %d logs 同樣是紫書上的題。 紫書上並沒有給出每一個三角形所貢獻的的權值的計算方法,我這裏就擅作主張,定義成點權的乘積和好了。 那麽做法是DP,這裏註意設狀態的方式(我這麽設是為了使需要求解的問題
bzoj4449: [Neerc2015]Distance on 點分治 三角剖分 平面圖與對偶圖
bzoj4449: [Neerc2015]Distance on Triangulation Description 給定一個凸n邊形,以及它的三角剖分。再給定q個詢問,每個詢問是一對凸多邊行上的頂點(a,b),問點a最少經過多少條邊(可以是多邊形上的邊,也可以是剖分上的邊)可以
凸多邊形最優三角剖分(演算法設計:動態規劃)
一、動態規劃 和分治法類似,把原問題劃分成若干個子問題,不同的是,分治法(子問題間互相獨立),動態規劃(子問題不獨立) 動態規劃: (1)找出最優解的性質,刻畫其結構特徵 (2)遞迴地定義最優值
PICK定理與三角剖分
//PICK定理:S=I+E/2-1,a多邊形內部的點數,b多邊形邊界上的點數,S多邊形的面積 #include <bits/stdc++.h> using namespace std; struct node{int x,y;}p[200]; int n,S,E,I;//N個點
6.Matplotlib繪圖--三角剖分圖
1.簡單的三角剖分: import matplotlib.pyplot as plt import numpy as np import random import matplotlib.tri as
動態規劃之凸多邊形最優三角剖分”
問題描述 多邊形是平面上一條分段線性的閉曲線。也就是說,多邊形是由一系列首尾相接的直線段組成的。組成多邊形的各直線段稱為該多邊形的邊。多邊形相接兩條邊的連線點稱為多邊形的頂點。若多邊形的邊之間除了連線頂點外沒有別的公共點,則稱該多邊形為簡單多邊形。一個簡單多邊形將平面分為3個部分:被包圍
2018.09.30【POJ3348】Cows(凸包)(三角剖分)
傳送門 解析: 讀優沒有寫負數又被卡了半個小時。。。 這裡採用JarrisJarrisJarris步進法求凸包。。主要講一講怎麼求多邊形面積。 思路: 滿足題意的顯然是這些點的凸包,而我們要做的就是求出凸包面積。 那麼怎麼求多邊形面積? 考慮三角剖分,我們將多
動態規劃-凸多邊形最優三角剖分問題
一、 問題描述 多邊形是平面上一條分段線性的閉曲線。也就是說,多邊形是由一系列首尾相接的直線段組成的。組成多邊形的各直線段稱為該多邊形的邊。多邊形相接兩條邊的連線點稱為多邊形的頂點。若多邊形的邊之間除了連線頂點外沒有別的公共點,則稱該多邊形為簡單多邊形。一個簡
動態規劃 凸 n 邊形三角剖分最小周長
題目輸入凸 n 邊形 p 1 ,p 2 ,··· ,p n , 其中頂點按凸多邊形邊界的逆時針序給出,多邊形中不相鄰頂點間的連線稱為弦。試設計一個動態規劃演算法,用若干條弦將凸邊形 p 1 ,p 2 ,··· ,p n 剖分成一些無公共區域的三角形,使得所有三角形的周長之和最
UVa 1331 最大面積最小的三角剖分(dp)
一共有4條邊,我們可以以隨意的順序切割,不過如果這樣的話,就會出現類似v0v3v4v6這樣的多邊形,這樣的多邊形很難用簡潔的狀態表示出來,這就是讓我一開始很糾結的地方。 其實我們會發現,對於同一種切割方法,我們可以有多種切割順序,但我們只要計算一種就好
凸多邊形最優三角剖分(動態規劃)
#include<stdio.h> #include<stdlib.h> #include<iostream> using namespace std; const int N=7; int Weight(int **w,int a,int b,int c) { r
【動態規劃】凸多邊形最優三角剖分
經典dp問題 1、問題相關定義: (1)凸多邊形的三角剖分:將凸多邊形分割成互不相交的三角形的弦的集合T。 (2)最優剖分:給定凸多邊形P,以及定義在由多邊形的邊和絃組成的三角形上的權函式w。要求確定該凸多邊形的三角剖分,使得該三角剖分中諸三角形上權之和為最小。